5.3 Accumulated Local Effects (ALE) Plot

Accumulated local effects30 は、特徴量が機械学習モデルの予測に対して、平均的にどの程度影響を与えているか示します。 ALE plot は、partial dependence plot (PDP) と比べて高速で偏りがありません。

PDP と ALE は目的が同じ手法なので、理解のしやすさのために、partial dependence plots の章 を先に読むことをおすすめします。 どちらも、ある特徴量が予測に対して平均的にどの程度の影響を与えるかを説明します。 次のセクションでは、特徴量が相関しているときに、partial dependence plot では深刻な問題があることを紹介します。

5.3.1 モチベーションと直感

もし機械学習モデルの特徴量が相関しているとき、partial dependence plot は信用できません。 他の特徴量と強く相関する特徴量に対する partial dependence plot の計算では、現実的に起こり得ない人工的なインスタンスの予測結果が含まれます。 これが、特徴量の効果を推定するときの大きなバイアスになります。

部屋の数とリビングのサイズによって家の値段を予測する機械学習モデルで partial dependence plot を計算することを考えてみてください。 今、リビングが、予測した値段に与える影響に関心があるとします。

Partial dependence plot の手順は 1) 特徴量を選ぶ 2) グリッドを決める 3) それぞれのグリッドの値に対して、 a) 特徴量をその値に変換し b) 予測を平均化する 4) 曲線を描く でした。 PDP の始めのグリッドの値(例えば 30m^2 )を計算するために、たとえ10部屋ある家でも「全ての」インスタンスに対して、30m^2 と置き換えます。 これは不自然な家です。 Partial dependence plot では、このような不自然な家があったとしても、それは問題がないとして特徴量の効果を推定します。 次の図は、2つの相関した特徴量と、partial dependence plot で現実的でないインスタンスを予測した平均の結果を示しています。

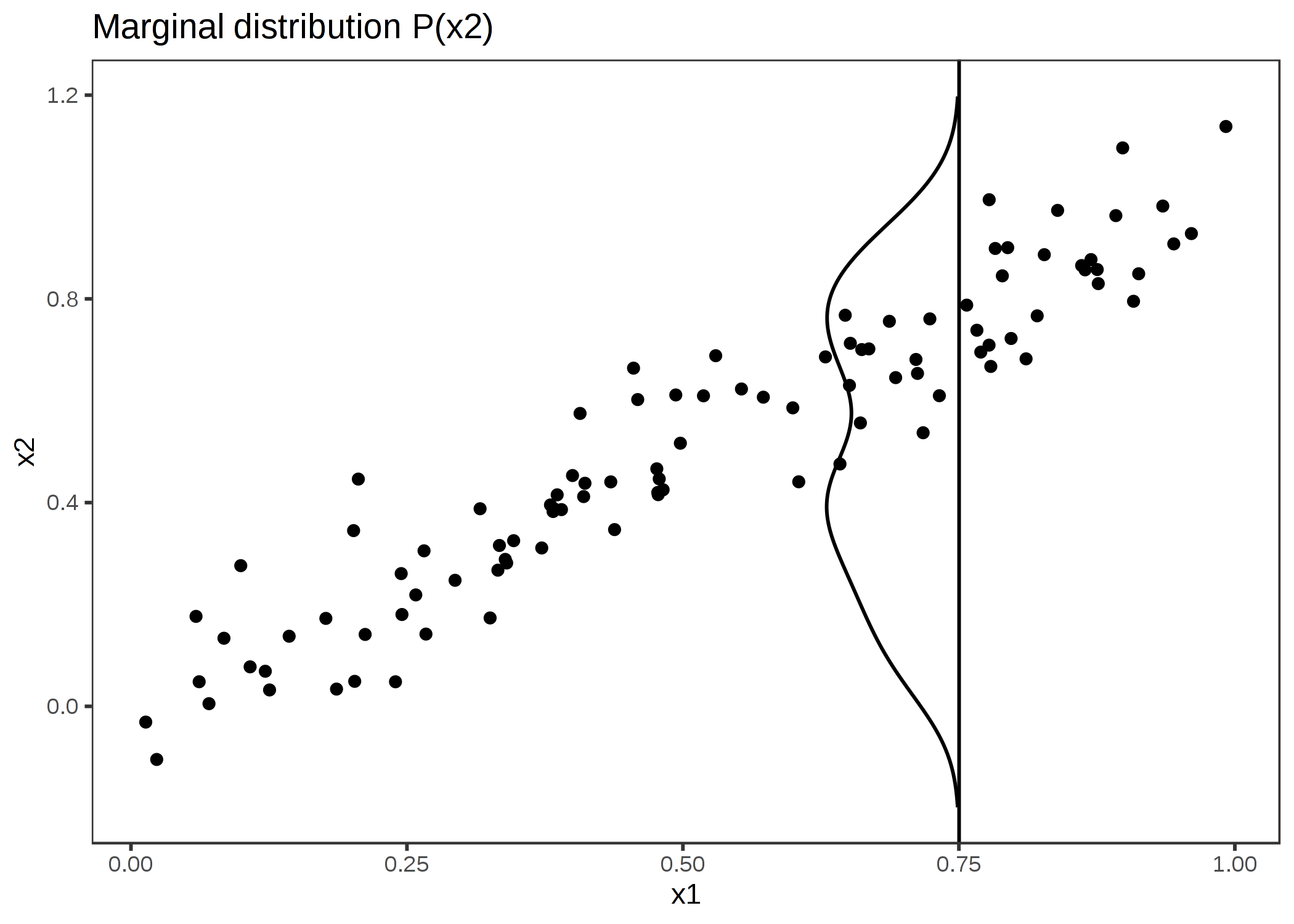
強く相関している特徴量 x1 と x2。 x1 が 0.75 の特徴量の影響を計算するために、PDP は全てのインスタンスの x1 を 0.75 に置き換え、x1=0.75 のときの x2 の分布が、全体の x2(縦軸) の分布と同じであると誤った仮定をしている。 これによって不自然な x1 と x2 の組み合わせ(例えば x2=0.2 で x1=0.75)が生まれ、PDP ではこれも平均効果の計算に含まれる。

FIGURE 5.10: 強く相関している特徴量 x1 と x2。 x1 が 0.75 の特徴量の影響を計算するために、PDP は全てのインスタンスの x1 を 0.75 に置き換え、x1=0.75 のときの x2 の分布が、全体の x2(縦軸) の分布と同じであると誤った仮定をしている。 これによって不自然な x1 と x2 の組み合わせ(例えば x2=0.2 で x1=0.75)が生まれ、PDP ではこれも平均効果の計算に含まれる。

特徴量同士の相関を保ったまま特徴量の影響の推定を得るためにはどうしたら良いでしょうか。 特徴量の条件付き分布上で周辺化します。つまり、x1 のグリッドの値では、x1 と似たような値を持つインスタンスの予測のみを用いて平均化します。 条件付き分布を使用して、特徴量の影響を計算する方法を Marginal Plot や M-Plot と呼びます(marginal distribution ではなく conditional distribution に基づいているのでややこしい名前です)。

待ってください、ALE plot について説明すると言っていたのではありませんでしたか。 実は、M-Plot は我々が求めている解決策ではありません。 なぜ M-Plot では問題を解決できないのでしょうか。

約 30 m2 の全ての家の予測を平均化してしまうと、相関が原因でリビングや部屋の数の「混合された」影響を推定してしてしまいます。 リビングが予測された家の価値に全く影響を与えないと仮定すると、部屋の数だけが価値に影響を与えます。 M-Plot はリビングのサイズが予測される価値を上げると示すでしょう、なぜなら部屋の数はリビングのサイズにしたがって増えていくからです。 次の図は2つの相関した特徴量に対して M-Plot がどう動くかを示しています。

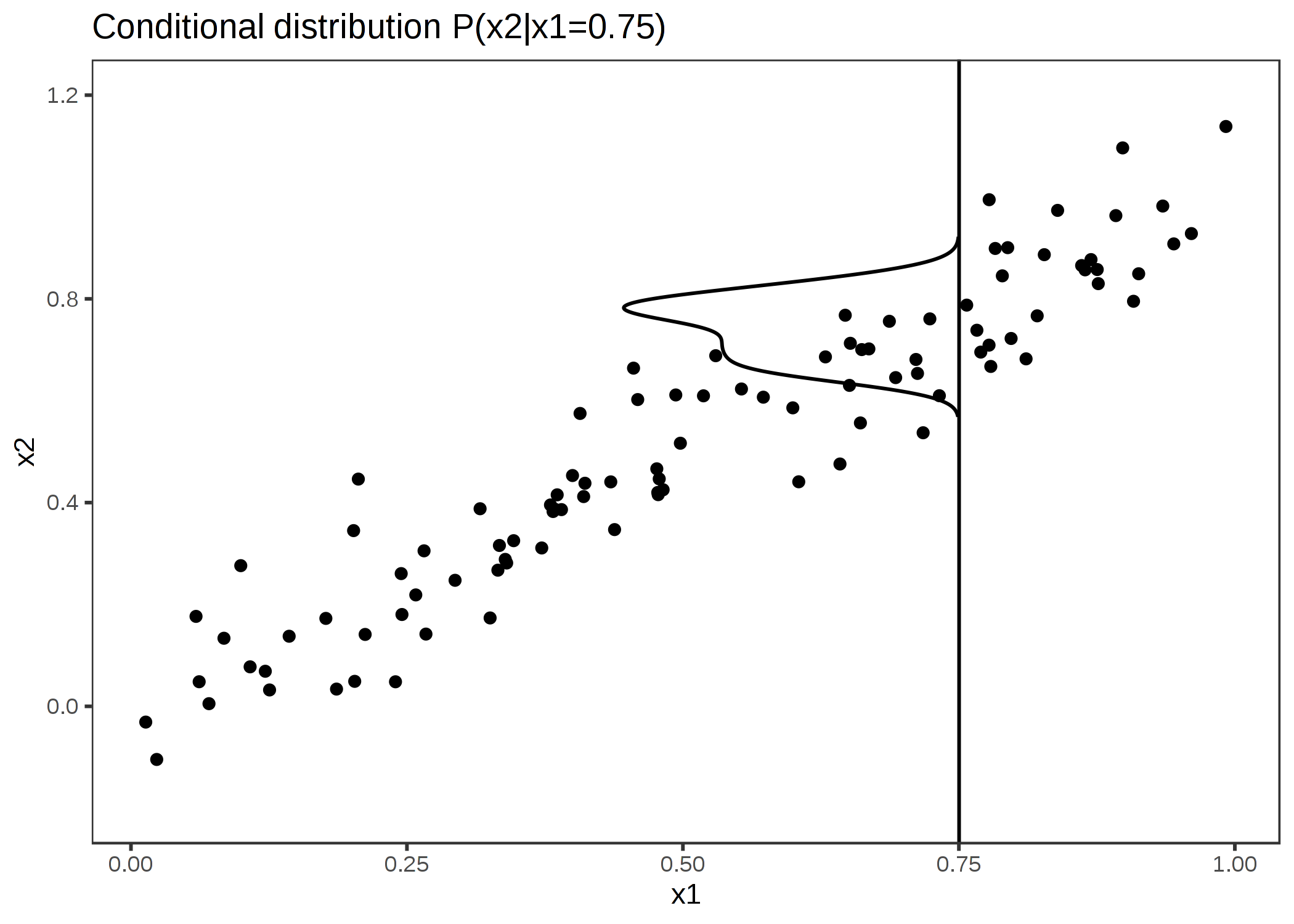
強く相関した特徴量 x1 と x2。 M-Plot は条件付き分布上で平均化する。ここで x1=0.75 のときの x2 の条件付き分布が示されている。局所的な予測を平均化することは両方の特徴量の影響を混ぜることにつながる。

FIGURE 5.11: 強く相関した特徴量 x1 と x2。 M-Plot は条件付き分布上で平均化する。ここで x1=0.75 のときの x2 の条件付き分布が示されている。局所的な予測を平均化することは両方の特徴量の影響を混ぜることにつながる。

M-Plot は現実的ではないインスタンスの予測を含めることを防ぎますが、ある特徴量の影響を他の相関する全ての特徴量の影響と混ぜてしまいます。 ALE plot では、 -- これも特徴量の条件付き分布に基づいている -- 予測の平均ではなく差分を計算することによってこの問題を解決しています。 30m2 のリビングの影響に対して、ALE はリビングが約 30m2 の家全てを使い、それらの家が31m2 だったとしたときの予測値からそれらの家が29m2 だったとしたときの予測値をひいたモデルの予測値を得ます。 これによって、リビングの広さの純粋な影響が得られ、かつ、他の相関した特徴量の影響とも混ざっていません。 差分を使うことにより他の特徴量の影響を受けないようにできます。 次の図から ALE plot がどのように計算されるか直感的に理解できるでしょう。

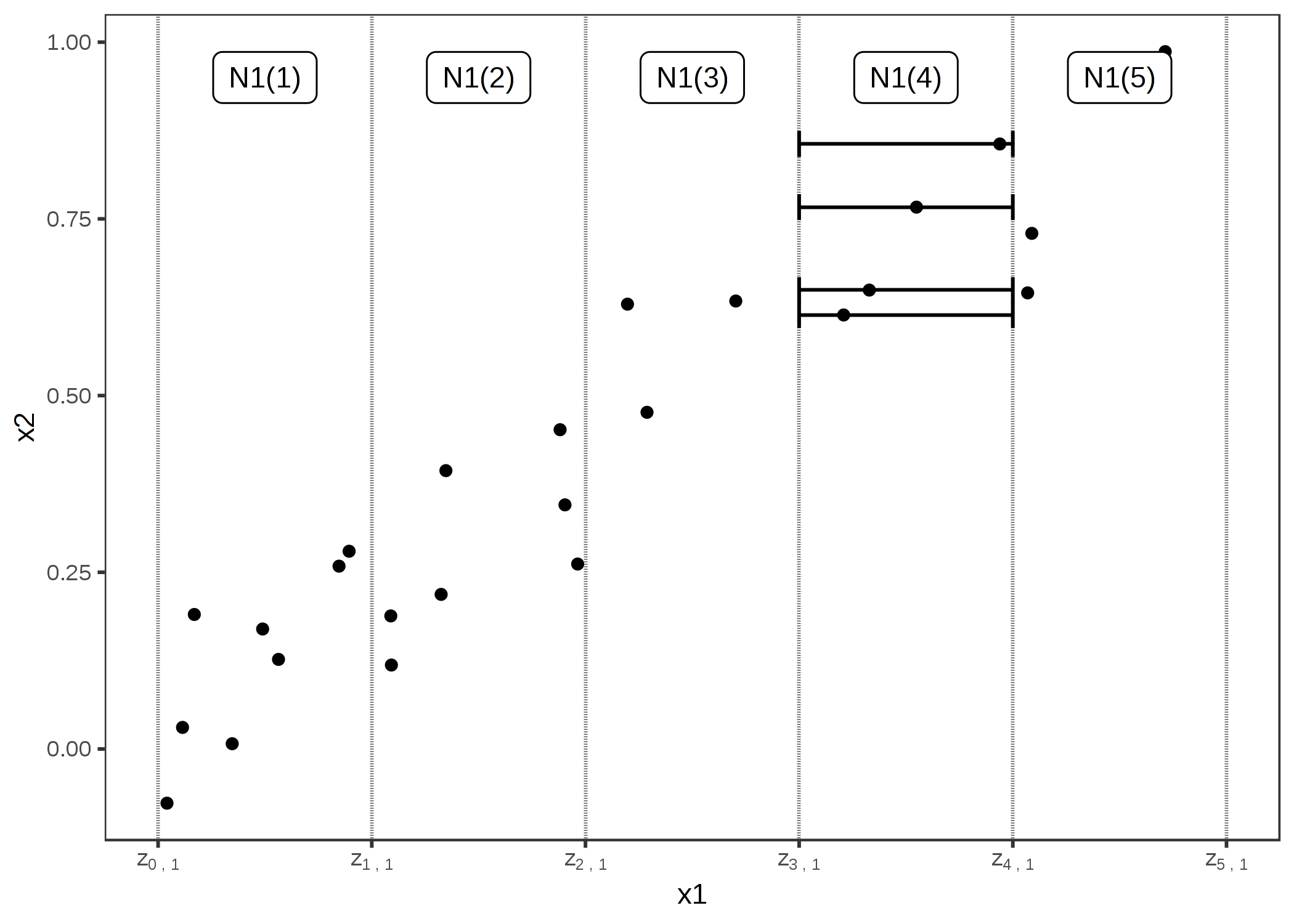
x2 と相関している特徴量 x1 の ALE の計算。はじめに x1 を区間(縦の線)に分ける。ある区間内のデータインスタンス(点)に対して、その特徴量をその区間の上限と下限の値に置き換えたときとの予測値の差分を計算する(横の線)。この差分は後に蓄積され、中心化して ALE 曲線となる。

FIGURE 5.12: x2 と相関している特徴量 x1 の ALE の計算。はじめに x1 を区間(縦の線)に分ける。ある区間内のデータインスタンス(点)に対して、その特徴量をその区間の上限と下限の値に置き換えたときとの予測値の差分を計算する(横の線)。この差分は後に蓄積され、中心化して ALE 曲線となる。

それぞれの プロット (PDP, M, ALE) が、ある特定のグリッドの値 v での、特徴量の影響をどのように計算するかを以下にまとめます。

Partial Dependence Plots: 「それぞれのインスタンスの特徴量の値を v としたときの、モデルの予測の平均を示します。ただし、特徴量の値を v にしたときのインスタンスが現実的であるかどうかは無視します。」

M-Plots: 「その特徴量が v に近い値を持つインスタンスに対する、モデルの予測の平均を示します。影響はその特徴量に起因しますが、相関する特徴量にも起因してしまいます。」

ALE plots: 「その特徴量が約 v であるインスタンスに対して、小さな"窓"の中でモデルの予測がどう変化するかを示します。」

5.3.2 理論

数学的に PDP, M-plot, ALE plot はどのように異なっているのでしょうか。 これら全てに共通していることは、複雑な予測関数 f を、1つか2つの特徴量に依存する関数に削減します。 3つの方法は全て、他の特徴量の効果を均すことによって関数を削減しますが、予測の平均、または予測の差を計算するかどうか、および平均を周辺分布、もしくは条件付き分布に対して行うかが異なります。

PDP は、周辺分布に対して予測を平均化します。

\[\begin{align*}\hat{f}_{x_S,PDP}(x_S)&=E_{X_C}\left[\hat{f}(x_S,X_C)\right]\\&=\int_{x_C}\hat{f}(x_S,x_C)\mathbb{P}(x_C)d{}x_C\end{align*}\]

これは、\(x_C\) の全ての特徴量で平均化された、特徴量 \(x_S\) での予測関数 f の値です。 平均化は、集合 C の特徴量に対する周辺化期待値 (marginal expectation) E を計算することを意味しており、これは、確率分布によって重み付けされた予測の積分です。 難しく聞こえますよね、しかし、周辺分布の期待値を計算するためには、単純に、全てのインスタンスを取り出して、これらの、集合 S 内の特徴量を特定のグリッドの値に書き換えます。そして、人工的に作ったデータセットの予測の平均を求めるだけです。 この手順が、特徴量の周辺分布に対して平均化した事を保証しています。

M-plots は条件付き分布に対して予測を平均化します。

\[\begin{align*}\hat{f}_{x_S,M}(x_S)&=E_{X_C|X_S}\left[\hat{f}(X_S,X_C)|X_S=x_s\right]\\&=\int_{x_C}\hat{f}(x_S,x_C)\mathbb{P}(x_C|x_S)d{}x_C\end{align*}\]

PDP と比較した時の唯一の違いは、興味のある特徴量の各グリッドの値で、周辺分布を仮定するのではなく、条件付き分布に対する予測の平均を計算することです。 実際には、これは近傍を定義しなけらばらない事を意味します。 例えば、 予測された家の価値に 30 m2 が与えた影響を計算したい場合、全ての 28 m2 から 32 m2 の間にある家の予測を平均化します。

ALE plot は、予測の変化を平均し、グリッド上で累積します（計算の詳細は後述）。

\[\begin{align*}\hat{f}_{x_S,ALE}(x_S)=&\int_{z_{0,1}}^{x_S}E_{X_C|X_S}\left[\hat{f}^S(X_s,X_c)|X_S=z_S\right]dz_S-\text{constant}\\=&\int_{z_{0,1}}^{x_S}\int_{x_C}\hat{f}^S(z_s,x_c)\mathbb{P}(x_C|z_S)d{}x_C{}dz_S-\text{constant}\end{align*}\]

この式は M-Plots との3つの違いを明らかにします。 1つ目は、予測値そのものではなく、予測値の変化を平均化することです。 変化は、勾配として定義されます（しかし、後ほど、実際の計算では、区間上の予測の差と置き換えられます)。

\[\hat{f}^S(x_s,x_c)=\frac{\delta\hat{f}(x_S,x_C)}{\delta{}x_S}\]

2つ目の違いは、z に対するもう1つの積分です。 集合 S の特徴量の範囲にわたって局所勾配を累積することで、予測に対する特徴量の影響を知ることができます。 実際の計算では、 z は予測の変化を計算するために、区間のグリッドに置き換えられます。 直接、予測を平均化する代わりに、ALE では、特徴量 S で条件づけされた予測の差を計算し、効果を推定するために特徴量 S 上の勾配を積分します。 これは、馬鹿げた様に聞こえます。 微分と積分は、通常、互いに打ち消し合います。例えば、最初に引き算をして、同じ数字を足し算する様な物です。 なぜ、これが、ここでは意味をなすのでしょうか。 微分（または、区間の差）は対象の特徴量の効果を分離し、そして、相関した特徴量の影響を遮断するのです。

ALE plots と M-plotsの3つ目の違いは、結果から定数を引く事です。 このステップによって、データに対しての平均的な影響がゼロになるよう ALE plot が中心化されます。

問題が1つ残ります。 全てのモデルで勾配が使用できる訳ではありません。例えば、ランダムフォレストは勾配が計算できません。 しかし、実際の計算では、勾配を使うのではなく、区間を使用します。 もう少し、ALE plots の推定を深く見てみましょう。

5.3.3 予測

最初に、どの様に ALE plots が1つの量的特徴量に対して予測されるのかを説明します。次に、2つの量的特徴量に対して、そして、最後にカテゴリカル特徴量について説明します。 局所的な効果を予測するために、特徴量をいくつかの区間に分割し、そして、予測の差を計算します。

\[\hat{\tilde{f}}_{j,ALE}(x)=\sum_{k=1}^{k_j(x)}\frac{1}{n_j(k)}\sum_{i:x_{j}^{(i)}\in{}N_j(k)}\left[f(z_{k,j},x^{(i)}_{\setminus{}j})-f(z_{k-1,j},x^{(i)}_{\setminus{}j})\right]\]

この方程式を右端から読み解いてみましょう。 Accumulated local effect という名前が、この方程式の個々の要素を、とてもよく表しています。 基本的に ALE method は予測の差を計算します。それにより、対象の特徴量をグリッド値 z と置き換えます。 予測の差は、ある区間の中の個々のインスタンスに対して、特徴量が持つ効果となります。 右側の合計は、区間内の全てのインスタンスの効果を足し合わせたものであり、式の中では、近傍 \(N_j(k)\) として書かれています。 この区間内の予測の差の平均値を計算するために、合計値を区間内のインスタンス数で割ります。 区間内の平均値は、ALE という名前の Local という用語で表現されます。 左の総和の記号は、全ての区間において、平均効果を累積する事を意味します。 例えば、（中心化されていない）3番目のALEの特徴量は、1番目、2番目そして3番目の区間の効果の合計です。 ALE の Accumulated という用語はこれを表しています。

この効果は、平均がゼロとなるように中心化されます。

\[\hat{f}_{j,ALE}(x)=\hat{\tilde{f}}_{j,ALE}(x)-\frac{1}{n}\sum_{i=1}^{n}\hat{\tilde{f}}_{j,ALE}(x^{(i)}_{j})\]

ALEの値は、データの特定の値における予測の平均と比較したときの、特徴量の主な影響として解釈する事が出来ます。 例えば、\(x_j=3\) において、ALEの推定が -2 であるとは、j番目の特徴量が 3 のとき、予測は予測の平均よりも 2 下がるということを意味します。

特徴量の分布の分位数は、区間を決めるグリッドとして使用されます。 分位数を使用することで、各区間内に同じ数のインスタンスが存在することを保証できます。 ただし、分位数は、区間の長さがばらつく可能性があるという欠点もあります。 例えば、低い値が多く、高い値が少数のみであるような、対象の特徴量が特に偏っている場合、不自然な ALE plot になる可能性があります。

2つの特徴量の相互作用に対するALEプロット

ALEプロットは2つの特徴量の相互作用の影響も表すことができます。 計算方法は単一の特徴量に対するのものと同じですが、2次元における影響を考慮しなければならないため、インターバルの代わりに長方形セル(2次元の区間)を使用します。 また、全体の平均の効果を調整することに加えて、それぞれの特徴量の効果の調整も行います。 これは2つの特徴量に対するALEは、それぞれの特徴量の効果を含まない2次の効果を推定するということです。 言い換えると、2つの特徴量に対するALEは、2つの特徴量の追加の相互作用のみを表すということです。 2次元のALEプロットの式は長くて読みづらいため、掲載を控えます。 計算式に興味がある人は、原論文の式 (13) -- (16) を参照ください。 ここでは、2次のALEの計算は、直感を養うための視覚的な説明にとどめます。

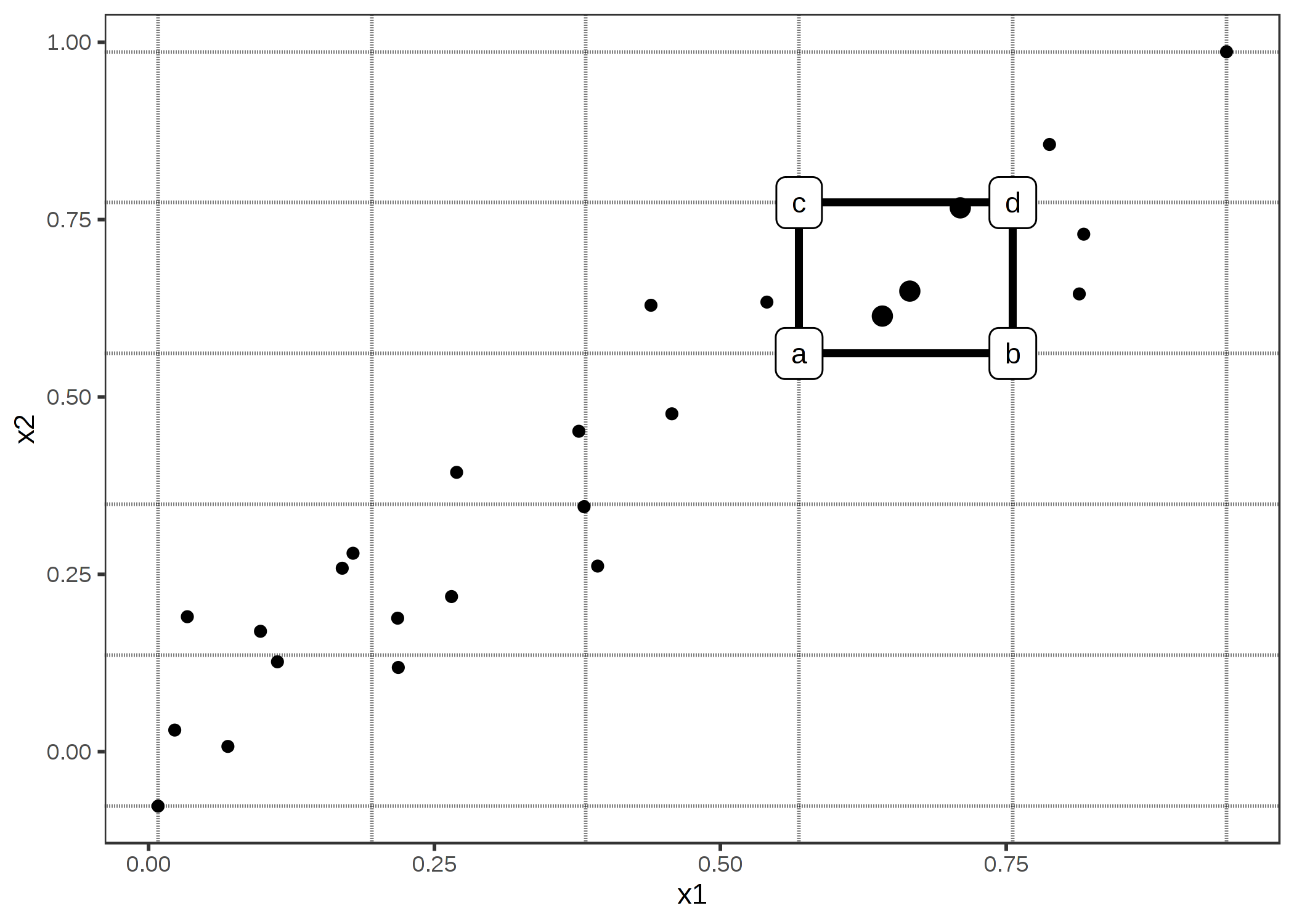
2次元ALEの計算。2つの特徴量に渡ってグリッド作成。それぞれのセルにおいて、グリッド内の全てのインスタンスに対して2次の差分を計算する。初めに x1 と x2 の値をセルの角の値で置き換える。a, b, c および d が(図中でラベル付けされているように)人工的なインスタンスの"角"での予測を表すとき、2次の差分は (d - c) - (b - a)となる。各セルにおける2次の差分の平均は、グリッド上のそれぞれのセルで累積されて中心化される。

FIGURE 5.13: 2次元ALEの計算。2つの特徴量に渡ってグリッド作成。それぞれのセルにおいて、グリッド内の全てのインスタンスに対して2次の差分を計算する。初めに x1 と x2 の値をセルの角の値で置き換える。a, b, c および d が(図中でラベル付けされているように)人工的なインスタンスの"角"での予測を表すとき、2次の差分は (d - c) - (b - a)となる。各セルにおける2次の差分の平均は、グリッド上のそれぞれのセルで累積されて中心化される。

前の図では、多くのセルが相関によって空となっていました。 ALEプロットでは、これがグレーまたは暗い色のボックスで可視化されます。 その代わりに、空のセルのALEの推定結果を、最も近い空でないセルの ALE の推定結果で置き換えることもできます。

2つの特徴量に対するALEの推定では、2つの特徴量の2次の効果のみを示しているため、解釈には特に注意が必要です。 2次の効果は、特徴量の主な効果を考慮した後の、追加の相互作用による影響です。 2つの特徴量は相互作用しないが、それぞれが予測結果に対して線形の影響を持つと仮定してください。 それぞれの特徴量に対する1次元のALEプロットでは、推定されたALE曲線は直線となるでしょう。 しかし2次元のALEの推定結果をプロットすると、2次の効果は相互効果による追加の影響のみを表すため、それらはゼロに近くなるはずです。 このような場合、ALEプロットとPDPは異なります。 PDPはいつも総合的な影響を可視化しますが、ALEプロットは1次または2次の影響のみ見せます。 それらは根底にある数学には依らない、設計における決まり事です。 純粋な主効果や2次の影響はPDPから低次の効果を差し引くことで計算可能であり、総合的な効果はALEプロットで低次の影響を引くのをやめることで得ることができます。

ALEは、任意の高次の計算 (3つ以上の相互作用) も可能ですが、PDPの章 でも触れたとおり、計算結果自体は意味の解釈が可能であっても可視化ができないので、2つの特徴量までにするべきです。

カテゴリカル特徴量に対するALE

ALEプロットは、-- 定義によると -- ある方向の中での影響を累積する手法であるため、特徴量の値の順序関係を要求します。 カテゴリカル特徴量は、自然な順序を持ちません。 カテゴリカル特徴量に対してALEプロットを計算するためには、何らかの方法で順序関係を作り出す、もしくは見出す必要があります。 カテゴリの順序は、ALEの解釈や計算方法に影響を与えます。

1つの解決法は、カテゴリを他の特徴量に対する類似度に従って順序づけることです。 2つのカテゴリ間の距離を、それぞれの特徴の距離の総和とします。 特徴量ごとの距離は、（量的特徴量における）Kolmogorov-Smirnov 距離 や (カテゴリカル特徴量における) 相対頻度表の両方のカテゴリの累積分布を比較します。 一度すべてのカテゴリ間の距離を計算してしまえば、multi-dimensional scaling を使って距離行列を1次元の距離尺度に削減できます。 これにより、カテゴリの類似度を基にした順序を得ることができます。

例を使用して、もう少し詳しくみてみましょう。 2つのカテゴリカル特徴量 "season" 、 "weather"、と 1つの量的特徴量 "temperature" を持つ場合を想定します。 最初のカテゴリカル特徴量 (season) に対して、ALEプロットを計算したいとします。 特徴量はカテゴリ、"spring", "summer", "fall", "winter" を持ちます。 "春" と "夏" のカテゴリ間の距離の計算を始めます。 距離は、気温と天気の特徴量の距離の総和です。 気温に関して、季節が "spring" の全てのインスタンスを取得し、累積分布関数を計算します。 "summer" を持つインスタンスに対しても同様に計算します。そして、それらの距離を Kolmogorov-Smirnov 統計により算出します。 天気に関しても、全ての "spring" のインスタンスに対して各天気ごとの確率を計算し、"summer" のインスタンスに対しても同様の計算を行ます。 その後、確率分布の絶対距離の総和を求めます。 もし、"spring" と "summer" が大きく異なる気温と天気を持つならば、合計のカテゴリの距離は大きくなります。 この処理を他の季節のペアでも繰り返し、得られた距離の行列を multi-dimensional scaling によって、1次元に削減します。

5.3.4 例

ALE プロットを実際に使用してみましょう。 PDP が失敗する状況を準備しました。 この状況では、予測モデルが2つの強く相関する特徴量から構成されています。 予測モデルはほとんど線形回帰モデルですが、インスタンスが観測されていない特徴量の組合わせの部分では奇妙なことになっています。

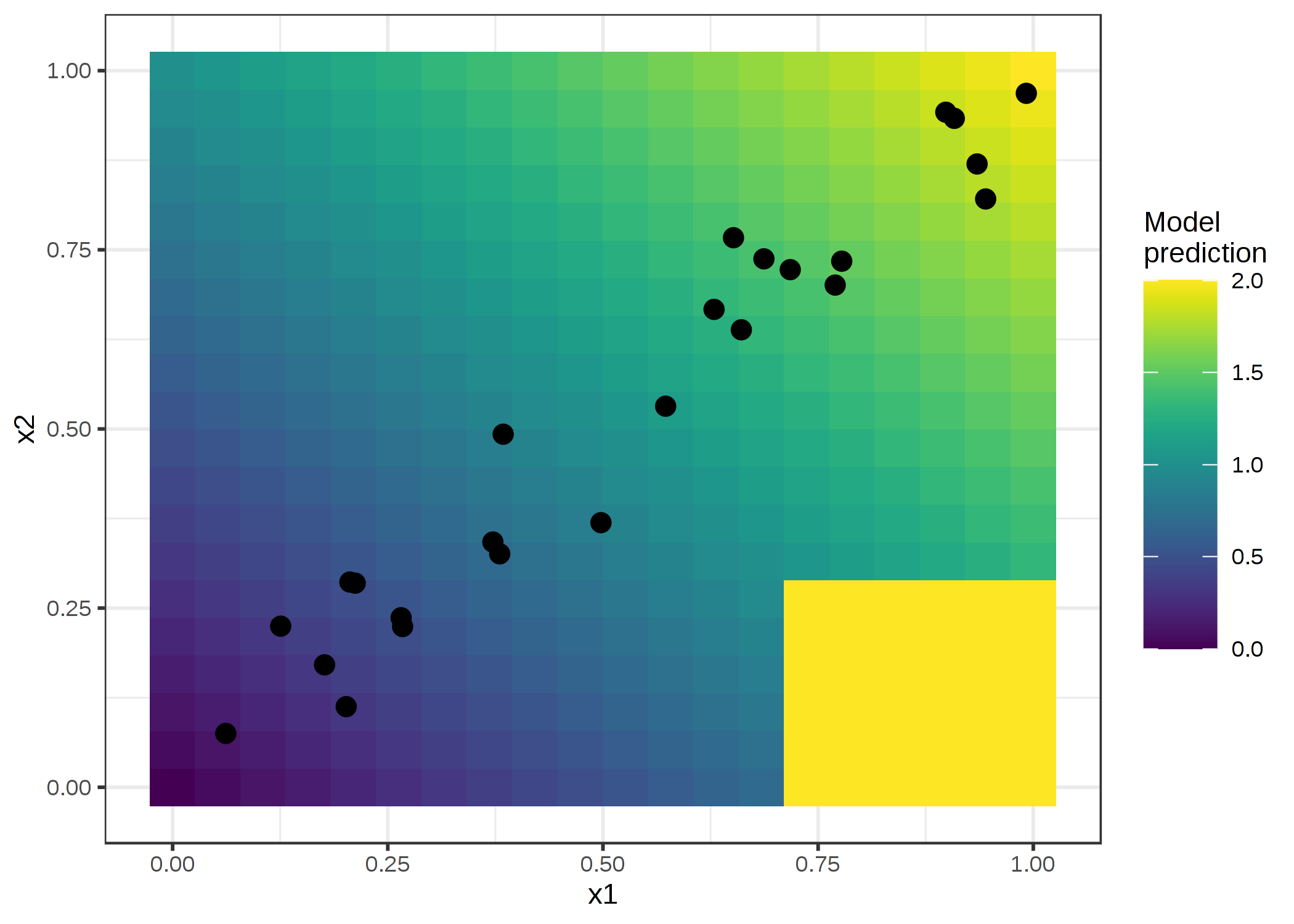
2つの特徴量と予測結果。このモデルは2つの特徴量の和を予測している(影の背景)が、x1>0.7, x2<0.3 の範囲では常に2と予測するという例外があります。この領域はデータの分布(点群)とかけ離れており、モデルの性能には影響しないが、解釈にも影響を与えるべきではない。

FIGURE 5.14: 2つの特徴量と予測結果。このモデルは2つの特徴量の和を予測している(影の背景)が、x1>0.7, x2<0.3 の範囲では常に2と予測するという例外があります。この領域はデータの分布(点群)とかけ離れており、モデルの性能には影響しないが、解釈にも影響を与えるべきではない。

これは現実的な状況でしょうか。 モデルを学習するとき、学習アルゴリズムは学習データの存在するインスタンスに対して誤差を最小化します。 奇妙な部分が学習データの分布の外側では起こりえます、なぜならモデルはその領域の奇妙なデータに対してペナルティを与えていないからです。 データ分布から離れることは外挿と呼ばれ、敵対的 サンプルの章で説明されているように、機械学習モデルをだますことにも 使用されます。 この例で、partial dependence plots が ALE plots と比べてどのように振る舞うか見てみましょう。

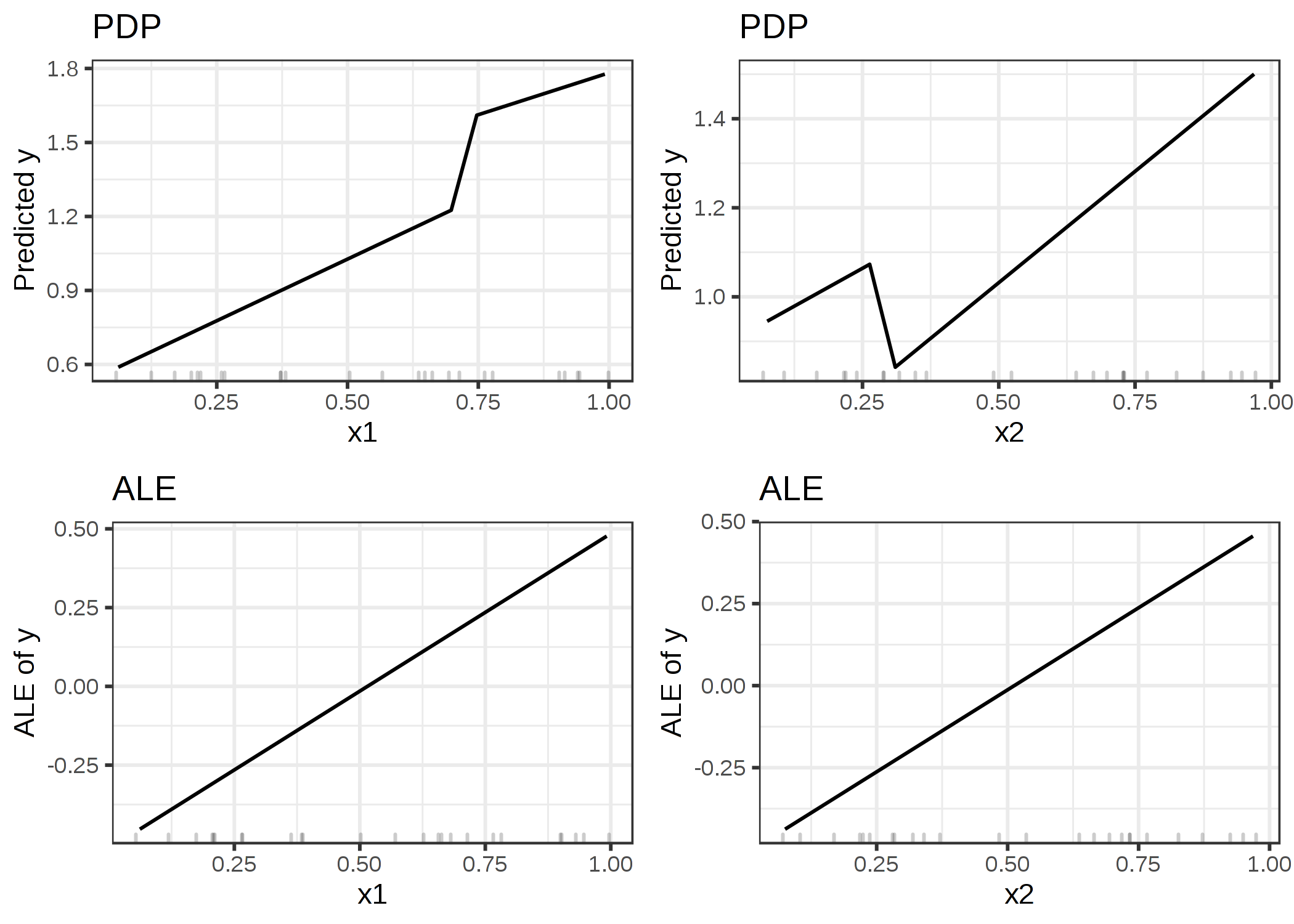
PDP(上の段)とALE(下の段)で計算される特徴量の影響の比較。 PDP の推定はデータ分布の外でモデルの奇妙な挙動に影響を受けている (プロットが跳ね上がっている)。ALE plot は機械学習モデルは特徴量と予測の間で関係が線形になっていると正しく認識できており、データがない領域を無視している。

FIGURE 5.15: PDP(上の段)とALE(下の段)で計算される特徴量の影響の比較。 PDP の推定はデータ分布の外でモデルの奇妙な挙動に影響を受けている (プロットが跳ね上がっている)。ALE plot は機械学習モデルは特徴量と予測の間で関係が線形になっていると正しく認識できており、データがない領域を無視している。

しかし、モデルが x1 > 0.7, x2 < 0.3 の領域での奇妙な振る舞いを知ることは、興味深いと言えないのでしょうか。 これは、どちらとも言えます。 なぜなら、これらのインスタンスは、現実的に起こり得ないのか、それともごく稀に起こりうるかであるので、一般的にはこのようなインスタンスを見るのは意味がありません。 テストデータの分布が多少異なり、いくつかのインスタンスがこの範囲に含まれるのであれば、この領域も特徴量の効果を計算する上で含めることをお勧めします。 ただし、このような、まだ観測がされていないデータの領域を含めるかどうかは意識的に決定できる必要があり、PDP のように手法の副作用となるべきではありません。 もし、モデルが異なる分布のデータで使われる可能性があるのであれば、ALE プロットを使用して可能性のあるデータ分布を用いてシミュレーションしてみることをおすすめします。

次は、現実のデータセットである、レンタル自転車数を天候と曜日に基づいて予測し、ALEプロットが本当に想定した通りに動いているか見てみましょう。 与えられた日のレンタル自転車数を予測するために回帰木を学習し、気温や相対湿度、風速が予測にどの程度影響を与えているか ALEプロットで分析してみます。 ALEプロットの結果を見てみましょう。

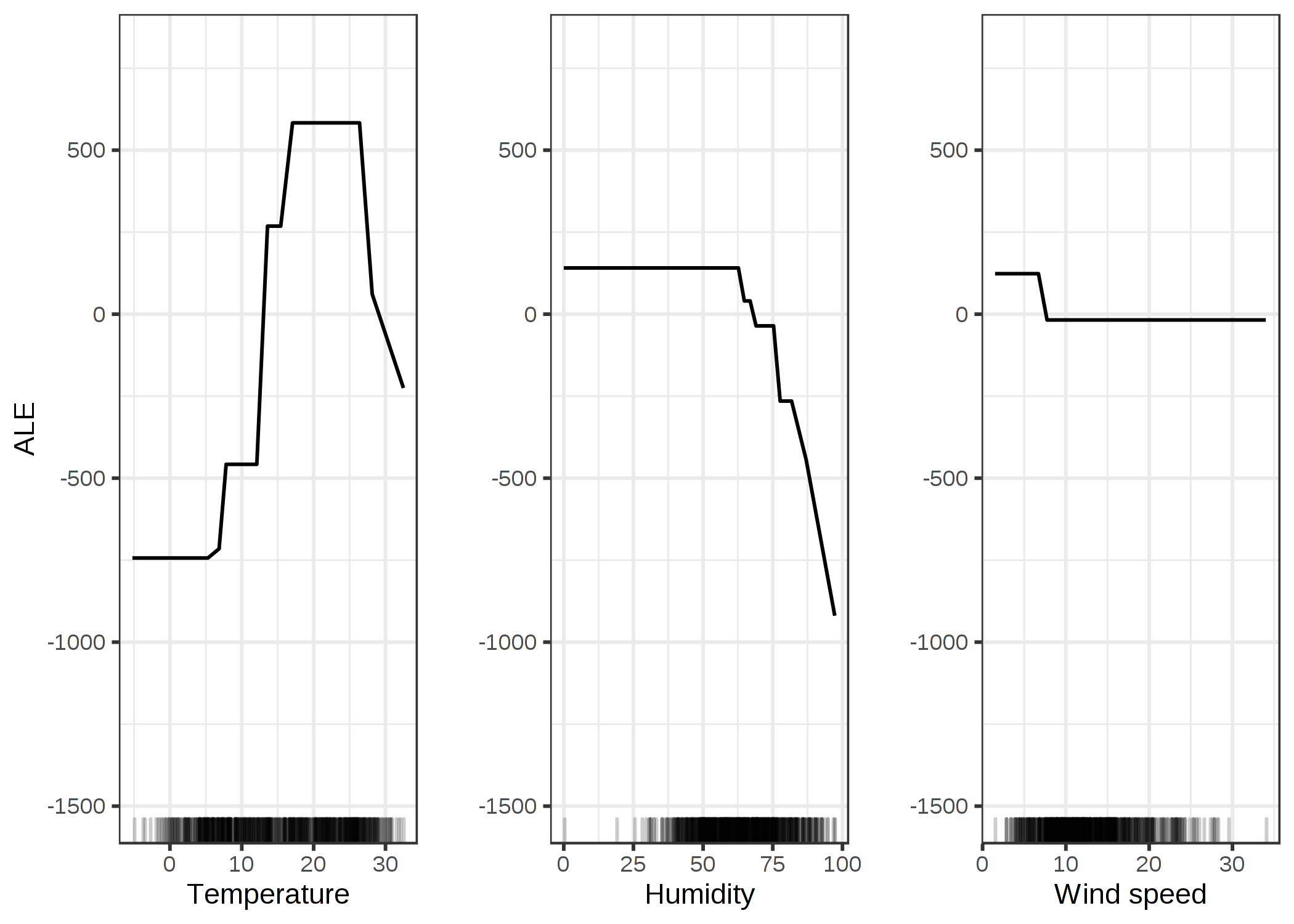
気温、湿度、風速による予測モデルに対する ALEプロット。気温は予測に大きく影響を与えています。予測の平均は気温の上昇に従って増えていますが摂氏25度を超えると下がる。湿度は負の影響を与えていて、60%以上では、相対湿度が高くなればなるほど、予測結果は小さくなる。風速は予測にはあまり影響を与えていない。

FIGURE 5.16: 気温、湿度、風速による予測モデルに対する ALEプロット。気温は予測に大きく影響を与えています。予測の平均は気温の上昇に従って増えていますが摂氏25度を超えると下がる。湿度は負の影響を与えていて、60%以上では、相対湿度が高くなればなるほど、予測結果は小さくなる。風速は予測にはあまり影響を与えていない。

気温、湿度、風速とその他全ての特徴量との相関を見てみましょう。 データはカテゴリカル特徴量を含んでいるため、量的特徴量間でのみ有効なピアソンの相関係数のみを使うことはできません。 代わりに、例えば気温に対して予測する線形モデルを他の特徴量を入力として学習させます。 そして、線形モデルの他の特徴量がどの程度分散を説明するか計算し、平方根を取ります。 もし、他の特徴量が量的特徴量であれば、結果はピアソンの相関係数の絶対値と一致します。 しかし、この "分散による説明" のモデルに基づくアプローチ (ANalysis Of VArianceを表してANOVAとも呼ばれます) は、カテゴリカル特徴量の場合でも有効です。 "分散による説明" の値は、0(無関係)と1(気温を他の特徴量から完全に予測できる) の間の値となります。 気温、湿度、風速と、その他の特徴量との間の因子寄与を計算します。 因子寄与(相関)が高くなればなるほど、PDP では大きな(潜在的な)問題となります。 次の図では、天候がその他の特徴量とどの程度強く相関しているかを可視化しています。

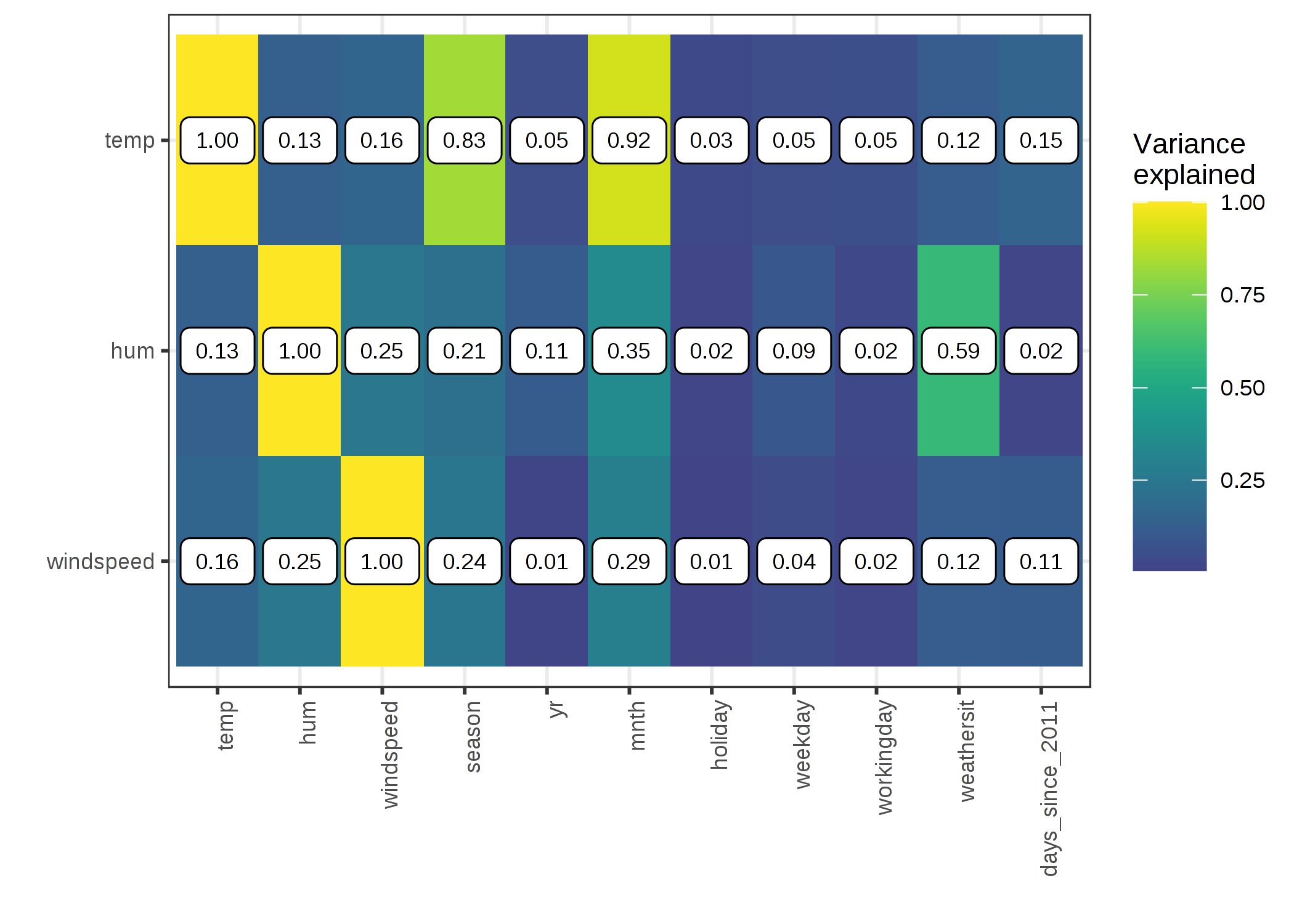
季節を特徴量として気温を予測する線形モデルを学習したときの、気温、湿度、風速とその他全ての特徴量との相関の強さを因子寄与で計算。気温については、-- 当然ながら -- 季節や月との高い相関が見られる。湿度は天候状況と相関している。

FIGURE 5.17: 季節を特徴量として気温を予測する線形モデルを学習したときの、気温、湿度、風速とその他全ての特徴量との相関の強さを因子寄与で計算。気温については、-- 当然ながら -- 季節や月との高い相関が見られる。湿度は天候状況と相関している。

この相関分析は 特に気温の特徴量に対して、partial dependence plots では、問題に直面するであろうことを明らかにしています。

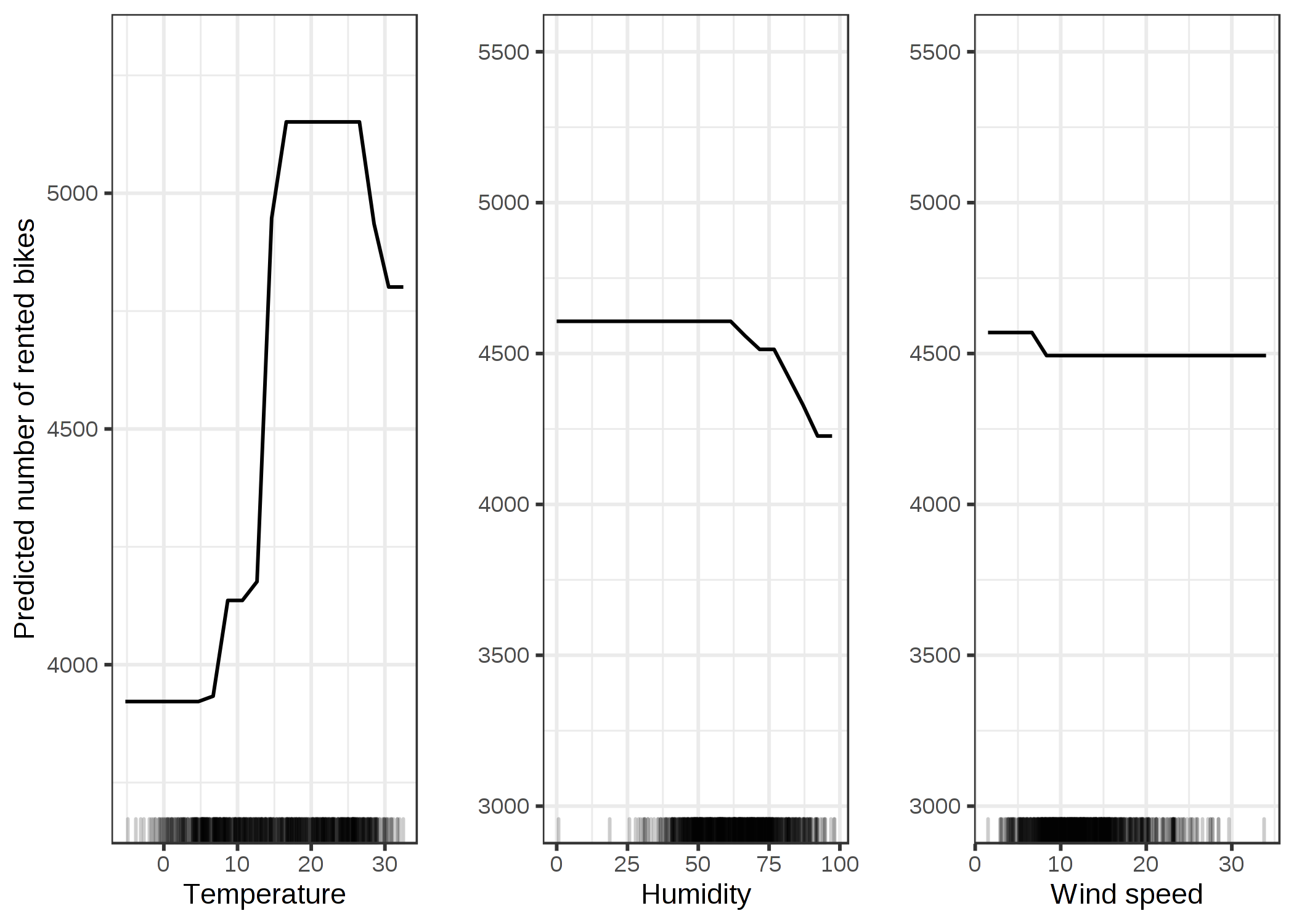
気温、湿度、風速に対する PDP。ALEプロットと比較すると、PDP は高気温または高湿度において予測自転車数が小さな減少を示している。PDPは、高気温の影響を計算するために、たとえそれが"冬"のインスタンスであっても全てのインスタンスを使う。ALEプロットの方が信頼性がある。

FIGURE 5.18: 気温、湿度、風速に対する PDP。ALEプロットと比較すると、PDP は高気温または高湿度において予測自転車数が小さな減少を示している。PDPは、高気温の影響を計算するために、たとえそれが"冬"のインスタンスであっても全てのインスタンスを使う。ALEプロットの方が信頼性がある。

次に、カテゴリカル特徴量に対する ALE プロットについて見てみましょう。 月は、レンタル自転車数への影響を分析したいカテゴリカル特徴量です。 ほぼ間違いなく、月は一定の並び(1月から12月まで)を既に持っていますが、初めに類似度によってカテゴリを並べ替えて、それから影響を計算したらどうなるか見てみましょう。 月は、気温や休日であるかといった他の特徴量に基づき、各月の日々の類似度によって並べられます。

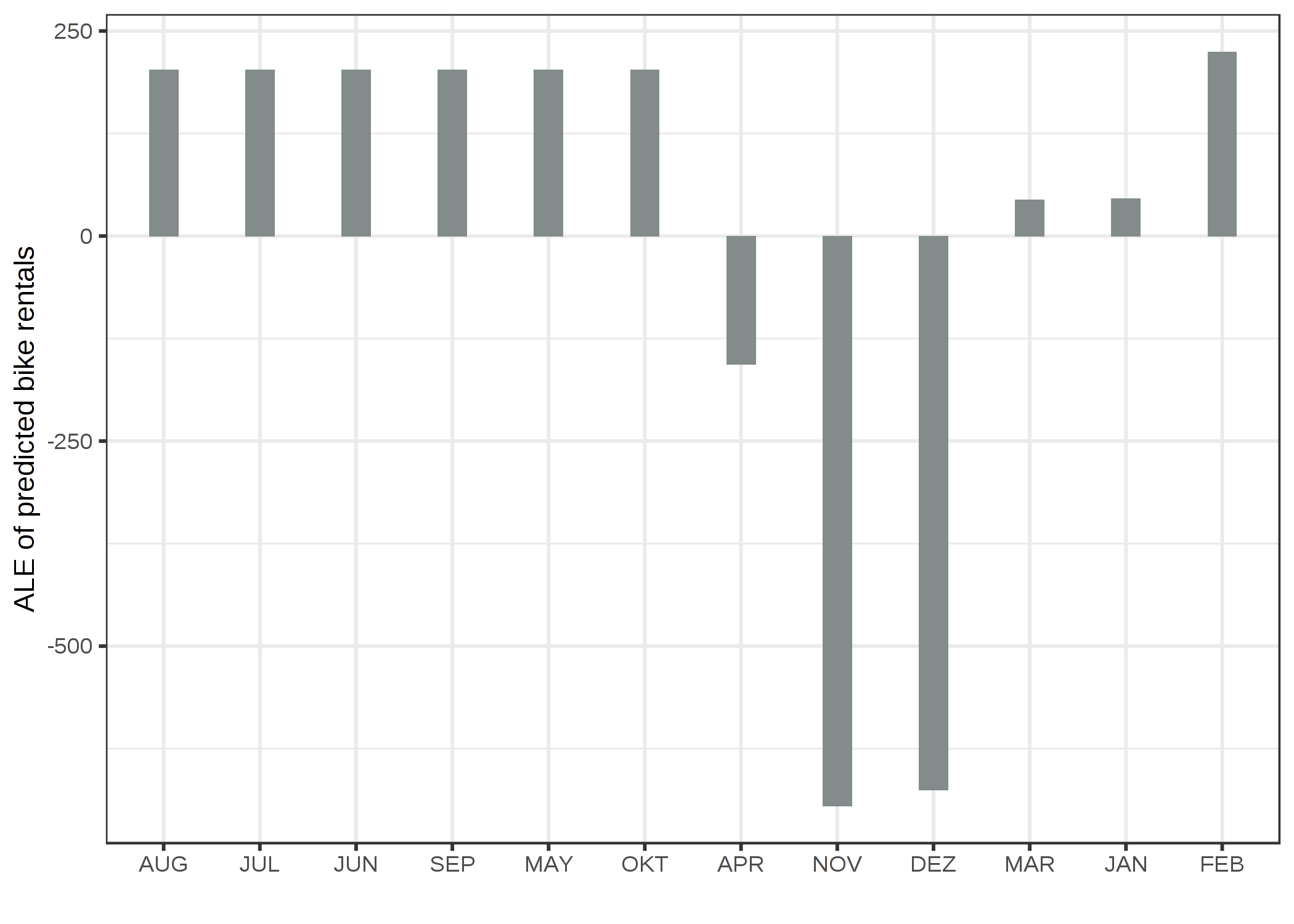
カテゴリカル特徴量である月についての ALE プロット。月はその他の特徴量における分布に基づく類似度によって並べられている。他の月と比較して、1月、3月、4月、特に12月と11月は、予測自転車数に低い影響を持つことが見て取れる。

FIGURE 5.19: カテゴリカル特徴量である月についての ALE プロット。月はその他の特徴量における分布に基づく類似度によって並べられている。他の月と比較して、1月、3月、4月、特に12月と11月は、予測自転車数に低い影響を持つことが見て取れる。

多くの特徴量は天候に関連することから、月の並びには月同士でいかに天候が似ているかが強く反映されています。 全ての寒い月は左側に(2月から4月)、暖かい月は右側に(10月から8月)あります。 ただし、天候以外の特徴量も類似度計算に含まれることに注意してください。例えば、休日の相対頻度は各月間の類似度計算において気温と同じ重みを持っています。

次に、予測自転車数における湿度と気温の2次効果を考えます。 2次効果は2つの特徴量における追加的な相互作用の影響であり、主効果を含まないことを思い出してください。 これは、例えば、高い湿度になると自転車レンタル予測数が平均的に下がるという効果が2次の ALE プロットでは見られなくなるということです。

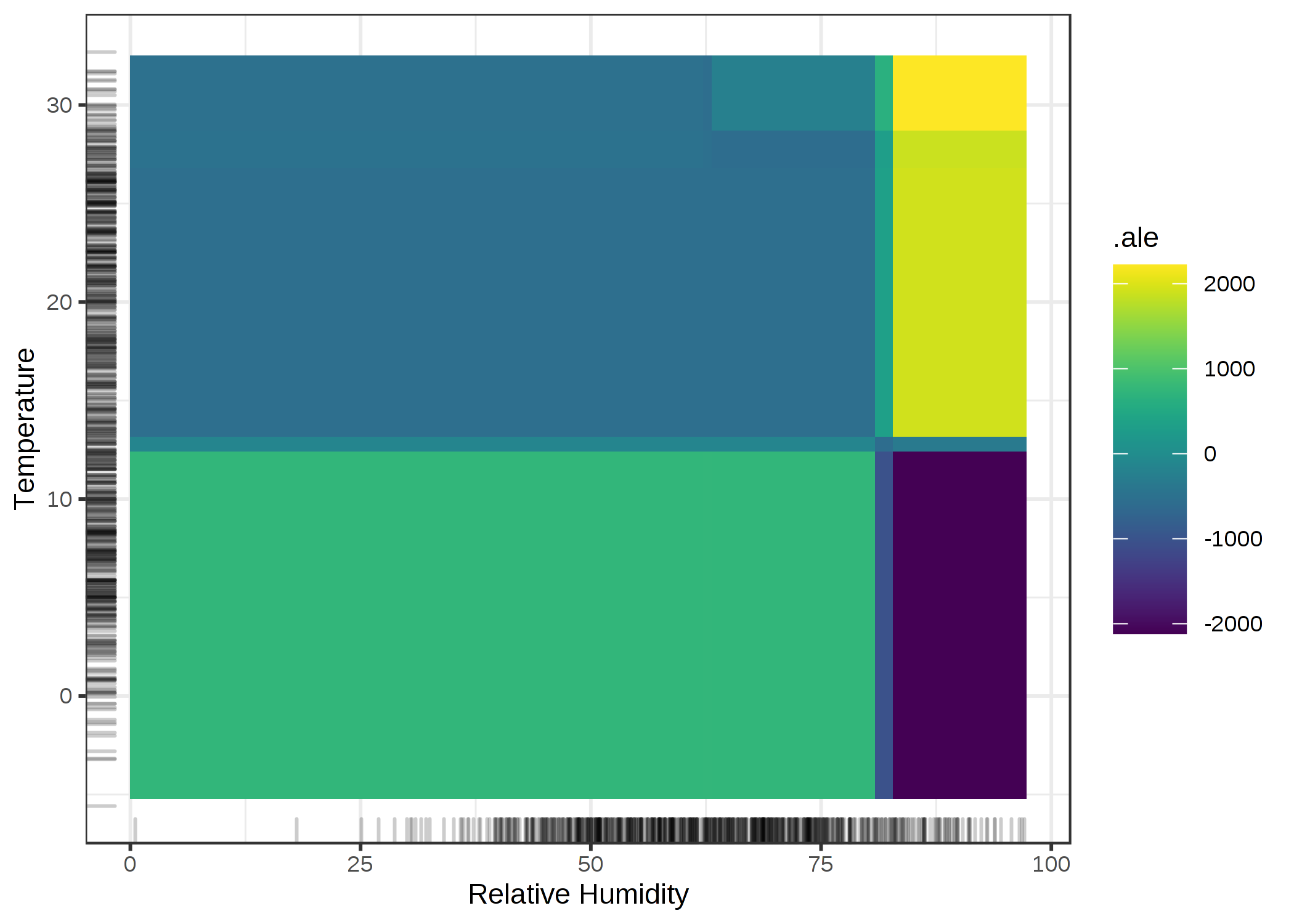
予測自転車数における湿度と気温の2次効果に対する ALE プロット。主効果を考慮した上で、明るい影は平均より上、暗い影は平均より下の予測であることを示す。プロットは気温と湿度の相互作用を明らかにする。暑くて湿った天候は予測数を増加させ、寒くて湿った天候は予測数に対して負の影響を示す。

FIGURE 5.20: 予測自転車数における湿度と気温の2次効果に対する ALE プロット。主効果を考慮した上で、明るい影は平均より上、暗い影は平均より下の予測であることを示す。プロットは気温と湿度の相互作用を明らかにする。暑くて湿った天候は予測数を増加させ、寒くて湿った天候は予測数に対して負の影響を示す。

気温と湿度の両方の主効果は、とても暑くて湿気のある天候では、予測されたバイクの数が減少する事を覚えておいてください。 したがって、暑くて湿気の多い天候において、気温と湿度は主効果の総和ではなく、それより大きいのです。 純粋な二次効果 (私たちが先ほど見た the 2D ALE plot) と全ての効果の間の差を強調するために、PDP を見てみましょう。 PDP は予測の平均、2つの主効果、二次効果 (相互作用) の全ての効果を表しています。

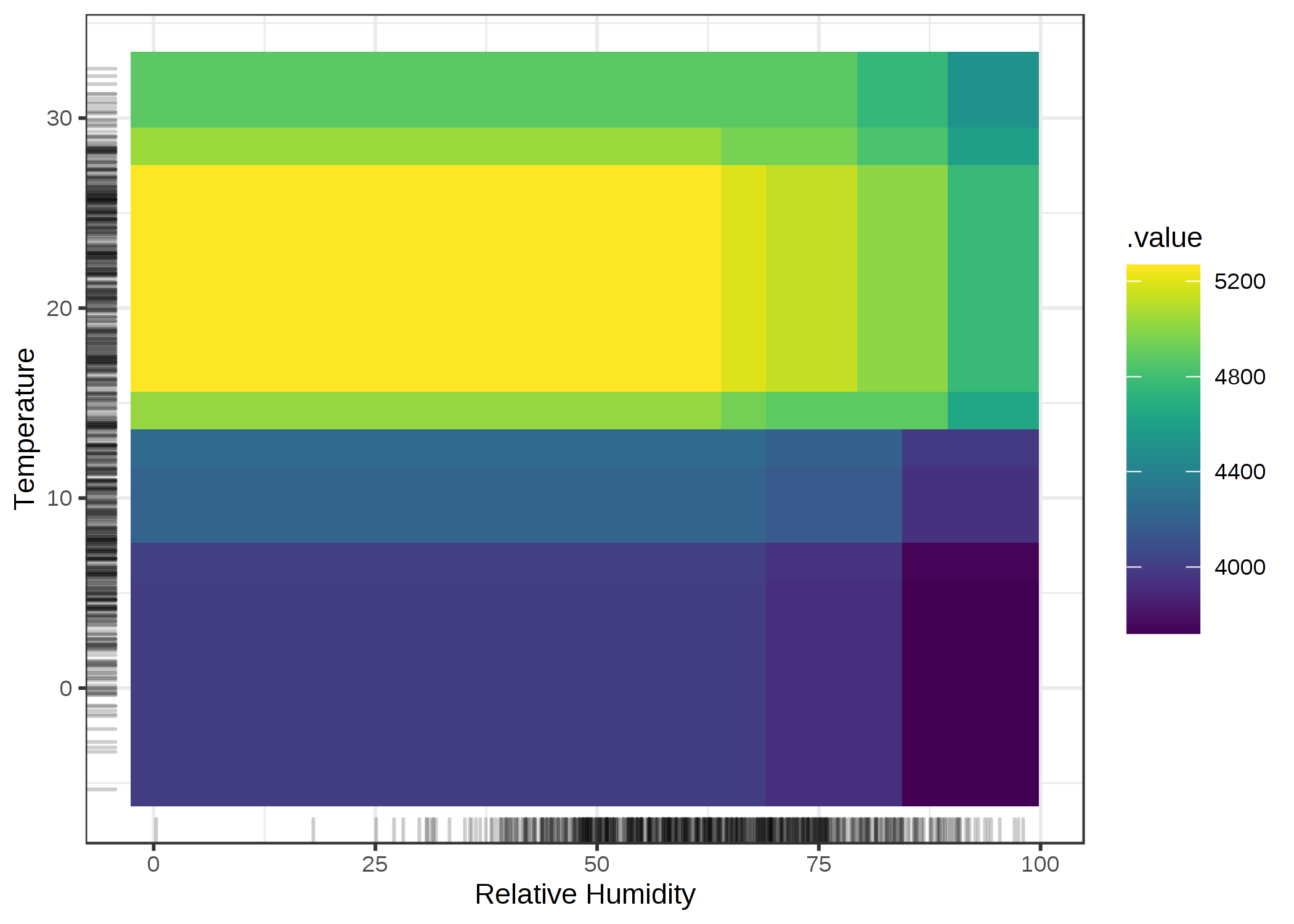
予測された自転車数に対する気温と湿度の全ての効果の PDP。プロットは、相互作用のみを示す 2DーALE plots とは対照的に、それぞれの特徴量の主効果と相互作用の影響が組み合わされている。

FIGURE 5.21: 予測された自転車数に対する気温と湿度の全ての効果の PDP。プロットは、相互作用のみを示す 2DーALE plots とは対照的に、それぞれの特徴量の主効果と相互作用の影響が組み合わされている。

もし相互作用のみに関心があるなら、主効果が混ざった全ての効果をみるのではなく、2次効果のみを見るべきです。 しかし、特徴量の組み合わさった影響を知りたいのであれば、PDP が示す全ての効果を見るべきです。 例えば、摂氏30度で湿度80%のときの自転車の予測台数を知りたいなら、2D PDP から直接読み取ることができます。 同じものを ALE plots から読み取ろうとすると、3つの plots を見る必要があります。 気温のみ、湿度のみ、気温と湿度の ALE plot から全体の予測平均を知る必要があります。 2つの特徴量の相互作用がない場合、単純な2つの主効果の積であるにもかかわらず、全ての効果は複雑な見た目になる可能性があり、誤解を招く恐れがあります。ただし、二次効果のみを見ることで、ただちに、相互作用がないことが示せるでしょう。

自転車の例はこれぐらいにして、クラス分類のタスクに移りましょう。 リスクの要因から 子宮頸がん の可能性を予測するランダムフォレストを学習します。 特徴量のうちの2つの ALE を可視化しましょう。

{r ale-cervical-1D, fig.cap = "子宮頸がんになる予測確率における年齢とホルモン避妊の年数の影響の ALE プロット。年齢の特徴量に関して、ALE plot は40歳までは平均してがんの確率が低く、それ以降は上昇することを示している。ホルモン避妊の年数が8年以降になると予測されるがんのリスクが高くなる傾向にある。"}
data(cervical)
cervical.task = makeClassifTask(data = cervical, target = "Biopsy")
mod = mlr::train(mlr::makeLearner(cl = 'classif.randomForest', id = 'cervical-rf', predict.type = 'prob'), cervical.task)

pred.cervical = Predictor$new(mod, data = cervical, class = "Cancer")
ale1 = FeatureEffect$new(pred.cervical, "Age", method = "ale")$plot()
ale2 = FeatureEffect$new(pred.cervical, "Hormonal.Contraceptives..years.", method = "ale")$plot() +
  scale_x_continuous("Years with hormonal contraceptives") +
  scale_y_continuous("")
gridExtra::grid.arrange(ale1, ale2, ncol = 2)

次に、妊娠回数と年齢の相互作用を見ます。

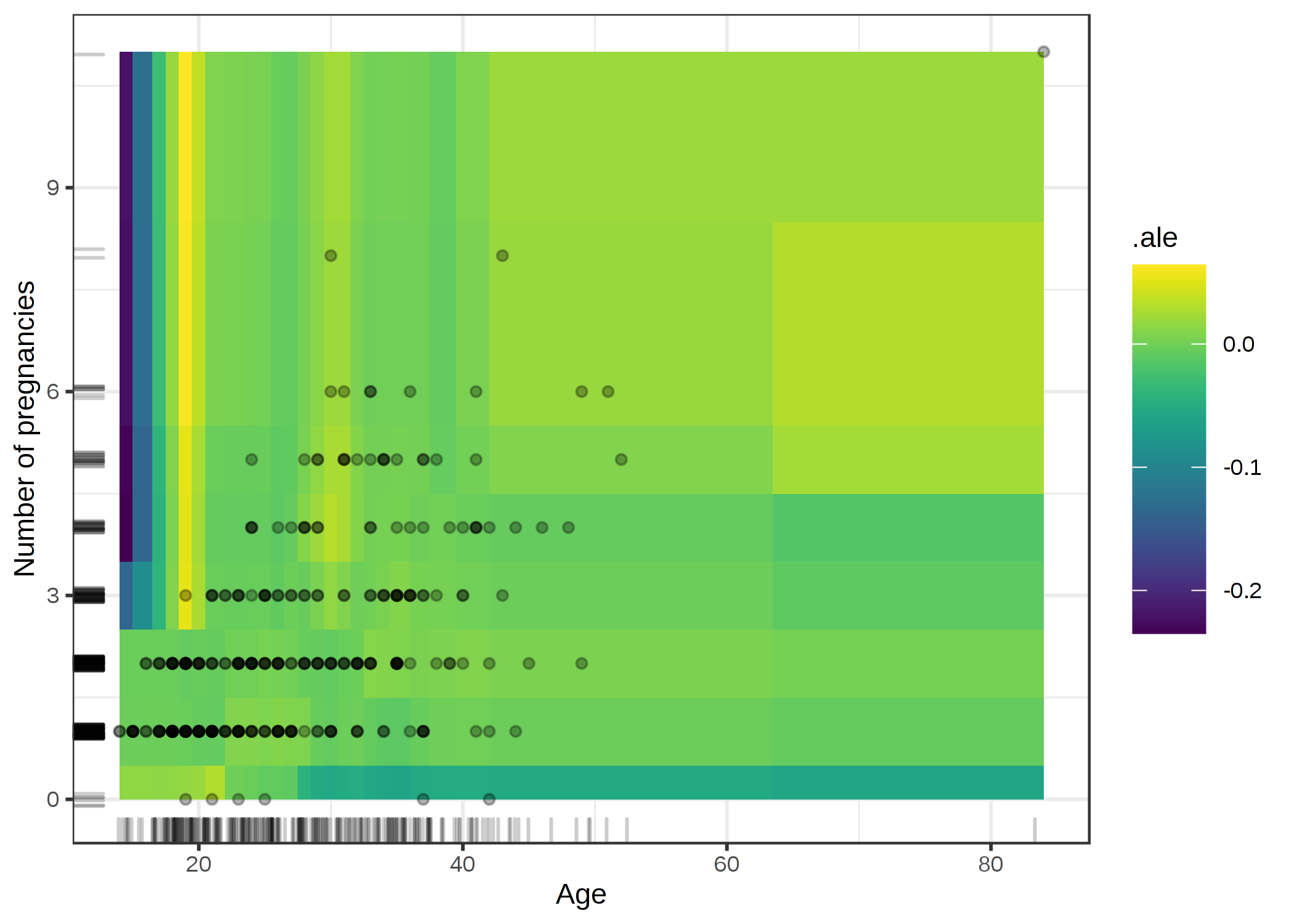
妊娠回数と年齢の2次効果に対するALEプロット。プロットの解釈は要領を得ず、過学習が発生している様子。例えば、18-20歳で3回以上の妊娠回数の場合に、プロットは妙なモデルの振る舞いを見せている(癌の確率が5%までの上昇をしている)。この区間の年齢と妊娠回数(点として表示しているデータ)の女性はデータ中で多くないため、学習時にこれらの女性に対して誤ったときの罰則が強く反映されていない。

FIGURE 5.22: 妊娠回数と年齢の2次効果に対するALEプロット。プロットの解釈は要領を得ず、過学習が発生している様子。例えば、18-20歳で3回以上の妊娠回数の場合に、プロットは妙なモデルの振る舞いを見せている(癌の確率が5%までの上昇をしている)。この区間の年齢と妊娠回数(点として表示しているデータ)の女性はデータ中で多くないため、学習時にこれらの女性に対して誤ったときの罰則が強く反映されていない。

5.3.5 利点

ALE plots は偏らない、つまり、ALE プロット は特徴量が相関している時でも機能します。 PDP は、相互作用があると、ありそうもない、または、現実的に不可能な特徴量の組み合わせを周辺化により作り出してしまうため、失敗します。 ALE プロットは PDP よりも計算が高速 で、最大の区間の数はインスタンスの数となるため、O(n) となります。PDP は、推定するグリッド点の数の n 倍の計算が必要です。 例えば、20 個のグリッド点の場合、ALE プロットでは、最悪でもインスタンスが含まれている区間の数だけ予測すればいいのに対して、PDPでは、20倍の予測を必要とします。

ALE プロットの解釈は明白です。与えられた値の条件の元、予測においての特徴量の変化の相対的な影響はALE plotsから読み解けます。 ALE プロット0に中心化されています。 ALE 曲線の各点での値は、予測平均との差なので、解釈がしやすくなります。 2D ALE プロットは相互作用のみ示します。 もし、2つの特徴量に相互作用がない場合、プロットは何も表示しません。

特徴量はたいてい、何らかの形で相関しているため、私はPDPよりも、ALE プロットを用いることを好みます。

5.3.6 欠点

ALE プロットは区間数が多いとき、少し不安定(値が上下する)になることがあります。 この場合、区間数を減らすことで、推定結果を安定にできますが、予測モデルの真の複雑さのいくつかを平坦化し隠してしまう恐れがあります。 区間の数を決める完璧な解決法はありません。 もし、インターバルの数が極端に少なけば、ALE プロットは正確ではないかもしれません。 もし、インターバルの数が極端に多いと、曲線はとても不安定になる事があります。

PDP とは違って、ALE プロットには ICE 曲線が付随していません。 PDP とっては、ICE curves は偉大です。なぜなら、特徴量中の不均一性を明らかにできるためであり、これは特徴量の効果がデータの一部で異なって見えるという事を意味します。 ALE プロットに対しては、インスタンス間で効果が異なるかを区間ごとに確認するしかありませんが、各区間には異なるインスタンスがあるため、ICE 曲線と同じではありません。

二次の ALE プロットは、特徴量の空間での安定性が異なっており、どの様な手法でもこれを可視化できません。 この理由としては、区間内の局所効果の推定時に、使用されるインスタンス数が異なっているからです。 結果として、全ての推定は異なる精度を持っています。（ただし、これは、最良の推定です。) この問題は、主効果ALEプロットのそれほど深刻ではないバージョンに存在します。 グリッドとして、分位数を使用しているため、全ての区間で同数のインスタンスが含まれています。しかし、いくつかの領域では、多くの短い区間になり、ALE 曲線はさらに多くの推定値から構成されます。 また、曲線の大部分を占める長い区間においては、インスタンス数は比較的少なくなります。 これは、例えば、年齢が高いときの子宮頸がん予測の ALE プロットで発生しました。

二次のALEプロットは、主効果を常に覚えておかなければいけないため、解釈するのに煩わしく感じるかもしれません。 ヒートマップを2つの特徴量の全体効果として読みたくなりますが、これは単に、相互作用による追加の効果でしかありません。 純粋な二次効果は、相互作用を発見するためには興味深いですが、その効果を理解するためには、主効果もプロットに統合する方が合理的だと考えます。

ALE plots の実装は、PDP に比べて、より複雑で、直感的でもありません。

特徴量が相関している場合、ALE plots はバイアスにかかっていませんが、特徴量が強く相関している場合、解釈は困難なままです。 なぜなら、もし、それらが強い相関を持っていた場合、個々の特徴量をそれぞれ変えていくのではなく、両方を同時に変える方が、効果を分析するためには、理にかなっているからです。 この欠点は ALE plots だけではなく、特徴量が強く相関している場合の一般的な問題です。

もし、特徴量が相関しておらず、計算にかかる時間が問題ではない時、PDPs が少し好まれます、なぜなら、PDP は理解しやすく、そして、ICE 曲線と共にプロットできるからです。

5.3.7 実装と代替手法

partial dependence plots と individual conditional expectation curves が代替手法であることについて説明していましたか？

私の知る限り、ALEプロットの実装は、R言語で、提唱者によって実装されたALEPlot R packageとiml packageがあります。

  1. Apley, Daniel W. "Visualizing the effects of predictor variables in black box supervised learning models." arXiv preprint arXiv:1612.08468 (2016).↩