4.6 RuleFit
Friedman と Popescu (2008)24 による RuleFit アルゴリズムは、相互作用効果を決定規則の形で自動的に検出したスパース線形モデルの学習に使われます。
線形回帰モデルは特徴間の相互作用を考慮していません。 線形モデルのようにシンプルで解釈しやすいモデルでありながら、特徴間の相互作用を統合したモデルがあれば便利ではないでしょうか? 実は、RuleFit はギャップを埋めることができます。 RuleFit は、元の特徴量と決定規則である多数の新しい特徴量を用いて、スパース線形モデルを学習します。 これらの新しい特徴量は、元の特徴量間の相互作用を説明します。 RuleFit は、決定木からこれらの特徴量を自動的に生成します。 分割された決定を結合し、規則にすることで、木を通る各パスを決定規則に変換できます。 ノードによる予測を破棄し、分割のみを決定規則に使用します。
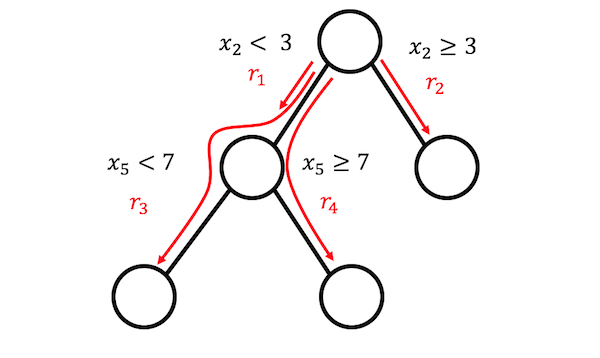
FIGURE 4.21: 3つの終端ノードを持つ木から4つの規則を生成することができます。
これらの決定木はどこから来ているのでしょうか? 決定木は興味のある結果を予測するために学習されます。 これは、予測問題に対して分割が意味を持つことを保証しています。 ランダムフォレストのように、多数の木を生成するアルゴリズムを RuleFit に使うことができます。 それぞれの木は、スパース線形回帰モデル (Lasso) で使用される追加の特徴量である決定規則に分解されます。
RuleFit が提案された論文では、ボストンの住宅データを使って説明しています。 目標は、ボストンの住宅の中央値を予測することです。 RuleFit で生成された規則の1つは、部屋の数 > 6.64 かつ 一酸化炭素濃度 < 0.67 であるならば 1、そうでないならば 0 としています。
RuleFit は、予測に重要な線形項や規則を特定するための重要度の指標としても機能します。 特徴量の重要度は回帰モデルの回帰係数から計算されます。 重要度の指標は元の特徴量("生"の形で使われ、多くの決定規則で使われる可能性があります)を集約したものになります。
RuleFit は、特徴量を変更することで、予測値の平均的な変化を示す partial dependence plot を導入します。 partial dependence plot は、どんなモデルにも使うことのできるモデル診断の手法であり、partial dependence plotsの章で解説されています。
4.6.1 解釈と例
RuleFit は最終的には線形モデルを推定するので、解釈は"普通の"線形モデルと同じになります。 違いは、決定規則からなる新しい特徴量を有していることです。 値が 1 であることは全ての条件を満たしていることを示し、そうでない場合は値は 0 になります。 RuleFit における線形項の解釈は、線形回帰モデルと同様になります。ある特徴量が 1 増加すると、予測結果は特徴量の重みに応じて変化します。
この例では、RuleFit をある日付のレンタル自転車数を予測するために使用しています。 この表は、RuleFit によって生成された5つの規則と、それらの Lasso による重みと重要性を示しています。 計算については、この章の後半で説明します。
| Description | Weight | Importance |
|---|---|---|
| days_since_2011 > 111 & weathersit in ("GOOD", "MISTY") | 793 | 303 |
| 37.25 <= hum <= 90 | -20 | 272 |
| temp > 13 & days_since_2011 > 554 | 676 | 239 |
| 4 <= windspeed <= 24 | -41 | 202 |
| days_since_2011 > 428 & temp > 5 | 366 | 179 |
最も重要な規則は "days_since_2011 > 111 & weathersit in ("GOOD", "MISTY")" であり、対応する重みは 793 です。 このような規則は、元の 8 つの特徴量から合計 278 個が作成されました。 かなりの数です! しかし Lasso のおかげで、278 のうち 58 だけが 0 ではない重みを持っていることがわかります。
大域的な特徴量の重要性を計算すると、気温と時間の傾向が最も重要な特徴量であることがわかります。
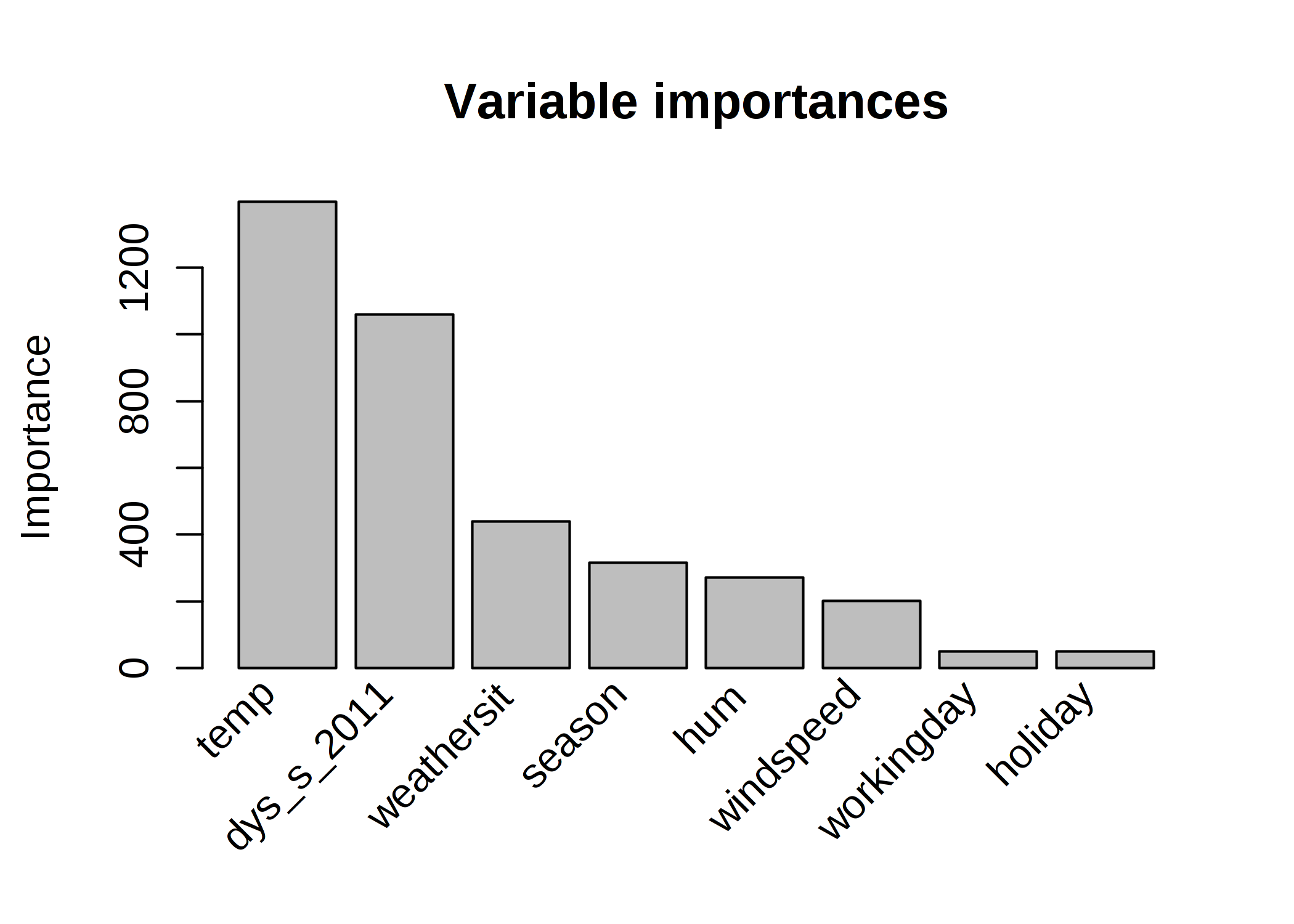
FIGURE 4.22: 自転車の数を予測する RuleFit モデルの特徴量重要度。予測のために最も重要な特徴量は気温と時間傾向でした。
特徴量重要度の尺度は、生の特徴量の重要度と、その特徴量が現れるすべての決定規則を含みます。
解釈のテンプレート
解釈は、線形モデルと類似しています。 他の特徴量が固定されている場合、特徴量 \(x_j\) が 1 変化すると、予測結果は \(\beta_j\) だけ変化します。 決定規則に関する重みの解釈は特殊です。 決定規則 \(r_k\) のすべての条件を満たすならば、予測結果は \(\alpha_k\) (線形モデルで学習された規則 \(r_k\) の重み) だけ変化します。
分類問題では(線形回帰ではなくロジスティック回帰を用いた場合)、 決定規則 \(r_k\) の全ての条件を満たすなら、その事象が発生するかしないかのオッズが \(\alpha_k\) 倍変化します。
4.6.2 理論
RuleFit アルゴリズムの技術的な詳細について深く見ていくことにしましょう。 RuleFit は2つのコンポーネントで構成されています。 最初のコンポーネントは、決定木から"規則"を作成し、2番目のコンポーネントでは、元の特徴量と作成した規則を入力とする線形モデルを学習します(これが "RuleFit" という名前の由来です)。
Step 1: 規則の生成
規則とはどのようなものでしょうか? アルゴリズムによって生成された規則は単純な形式になります。 例えば、IF x2 < 3 AND x5 < 7 THEN 1 ELSE 0 といったものです。 規則は、決定木を分解することで構築されます。 決定木上の任意のパスは、決定規則に変換できます。 規則のための木は、出力を予測するために利用されます。 したがって、分割や得られる規則は興味のある結果を得るために最適化されています。 特定のノードに至る二分決定を "AND" で連結させるだけで規則ができます。 多様かつ意味のある規則を多く生成することが望まれます。 勾配ブースティングでは、y を元の特徴量 X を使って回帰あるいは分類をすることで、決定木のアンサンブルを学習させます。 そして作成された各々の木は、複数の規則に変換されます。 ブースティングに限らず、任意の木のアンサンブルアルゴリズムに対して、RuleFit の木を生成できます。 木のアンサンブルは、次の一般的な式で記述できます。
\[f(x)=a_0+\sum_{m=1}^M{}a_m{}f_m(X)\]
M は木の数であり、\(f_m(x)\) は m 番目の木の予測関数です。 \(a\) は重みです。 Bagged ensembles、ランダムフォレスト、AdaBoost、そして MART は木のアンサンブルを生成し、RuleFit で使用されます。
アンサンブルの全ての木から規則を作成します。 各規則 \(r_m\) は次の形式で表されます。
\[r_m(x)=\prod_{j\in\text{T}_m}I(x_j\in{}s_{jm})\]
ここで、\(\text{T}_{m}\) は、m 番目の木で利用される特徴量の集合です。 I は、特徴量 \(x_j\) が j 番目の特徴量(木の分割で指定されたもの)に対する部分集合 s に含まれる場合に 1、それ以外の場合に 0 となる指示関数です。 量的特徴量の場合、\(s_{jm}\) は特徴量の値の区間となります。 区間は次の2つの場合のいずれかのようになります。
\[x_{s_{jm},\text{lower}}<x_j\]
\[x_j<x_{s_{jm},upper}\]
特徴量を更に分割すると、より複雑な区間になる可能性があります。 カテゴリカル特徴量の場合、部分集合は特徴量の特定のカテゴリが含まれることになります。
自転車レンタルのデータセットの例を見てみましょう。
\[r_{17}(x)=I(x_{\text{temp}}<15)\cdot{}I(x_{\text{weather}}\in\{\text{good},\text{cloudy}\})\cdot{}I(10\leq{}x_{\text{windspeed}}<20)\]
この規則は、3つの条件全てが満たされた場合に 1、それ以外は 0 を返します。 RuleFit は、葉だけではなく、木の全てのノードから規則を抽出します。 したがって、作成されるであろう規則は次のようになります。
\[r_{18}(x)=I(x_{\text{temp}}<15)\cdot{}I(x_{\text{weather}}\in\{\text{good},\text{cloudy}\}\]
全体として、\(t_m\) 個の葉をもつ M 個の木のアンサンブルから作成される規則の数は次式で与えられます。
\[K=\sum_{m=1}^M2(t_m-1)\]
RuleFit の著者によって導入されたトリックは、ランダムな深さの木を学習することで、長さの異なる多種多様な規則を生成するというものです。 各ノードにおける予測値は破棄して、そのノードに至る条件のみを保持し、そこから規則を作るということに注意してください。 決定規則の重みづけは、RuleFit の第2ステップで行われます。
ステップ1はこのように見ることもできます。 RuleFit は、元の特徴量から新しい特徴量の集合を生成します。 これらの特徴量は、二値であり、元の特徴量の極めて複雑な相互作用を表現できます。 規則は予測タスクで最良の結果が得られるように選択されます。 規則は、共変量行列Xから自動的に生成されます。 規則は元の特徴量に基づく新たな特徴量としてみなすことができます。
Step 2: スパース線形モデル
ステップ1で、多くの規則を得ることができます。 この最初のステップは、単なる特徴量の変換にすぎないため、モデルへの適合はまだ終わっていません。 また、規則の数を減らしたいとも思うでしょう。 これらの規則に加えて、元のデータセットの全ての"生"の特徴量も、スパース線形モデルで利用することになります。 全ての規則と元の特徴量が線形モデルの特徴量となり、重みが推定値されます。 元の生の特徴量を追加するのは、木は y と x の間の単純な線形関係を表現するのに失敗するためです。 スパース線形モデルを学習する前に、元の特徴量の外れ値をクリッピング (winsorizing) し、外れ値に対してより頑健になるようにします。
\[l_j^*(x_j)=min(\delta_j^+,max(\delta_j^-,x_j))\]
ここで、\(\delta_j^-\) と \(\delta_j^+\) は、特徴量 \(x_j\) のデータ分布の \(\delta\) 分位数です。 \(\delta\) に0.05を選択すると、上位 5% または下位 5% の特徴量 \(x_j\) の値が、それぞれ 5% または 95% の分位数に設定されます。 経験則として、\(\delta\) = 0.025 を選択できます。 さらに、線形項は、通常の決定規則と事前の重要性が同一となるように正規化する必要があります。
\[l_j(x_j)=0.4\cdot{}l^*_j(x_j)/std(l^*_j(x_j))\]
\(0.4\) は、\(s_k\sim{}U(0,1)\) の一様なサポート分布を持つ規則の標準偏差の平均です。
両方のタイプの特徴量を組み合わせて、新たな特徴量行列を作成し、次の形式で Lasso を利用してスパース線形モデルを学習します。
\[\hat{f}(x)=\hat{\beta}_0+\sum_{k=1}^K\hat{\alpha}_k{}r_k(x)+\sum_{j=1}^p\hat{\beta}_j{}l_j(x_j)\]
ここで、\(\hat{\alpha}\) は、規則の特徴量に対して推定された重みベクトルであり、\(\hat{\beta}\) は、元の特徴量に対する重みベクトルです。 RuleFit は Lasso を利用するため、損失関数は、一部の重みを 0 にするための制約が必要になります。
\[(\{\hat{\alpha}\}_1^K,\{\hat{\beta}\}_0^p)=argmin_{\{\hat{\alpha}\}_1^K,\{\hat{\beta}\}_0^p}\sum_{i=1}^n{}L(y^{(i)},f(x^{(i)}))+\lambda\cdot\left(\sum_{k=1}^K|\alpha_k|+\sum_{j=1}^p|b_j|\right)\]
この結果は、元の全ての特徴量と規則に対して線形な効果をもつ線形モデルです。 解釈は、線形モデルの場合と同様ですが、唯一の違いは、一部の特徴量が二値の規則となっている点です。
Step3(optional): 特徴量重要度
元の特徴量の線形項については、標準化された予測器を利用して特徴量重要度を測定します。
\[I_j=|\hat{\beta}_j|\cdot{}std(l_j(x_j))\]
ここで、\(\beta_j\) は、Lasso モデルから得られた重みであり、\(std(l_j(x_j))\) はデータ全体の線形項の標準偏差です。
決定規則の項の場合、重要度は次式で計算されます。
\[I_k=|\hat{\alpha}_k|\cdot\sqrt{s_k(1-s_k)}\]
ここで、\(\hat{\alpha}_k\) は、決定規則の関連するLassoの重みであり、\(s_k\) は、データにおける特徴量のサポートであり、決定規則が適用されるデータの割合です(ここで、\(r_k(x)=1\) )。
\[s_k=\frac{1}{n}\sum_{i=1}^n{}r_k(x^{(i)})\]
特徴量は線形項として現れるだけでなく、場合によっては多くの決定規則の内部にも現れます。 どのように特徴量の重要度を測るべきでしょうか? 特徴量の重要度 \(J_j(x)\) は、個々の予測ごとに測定できます。
\[J_j(x)=I_j(x)+\sum_{x_j\in{}r_k}I_k(x)/m_k\]
ここで、\(I_l\) は線形項の重要度、\(I_k\) は \(x_j\) が現れる決定規則の重要度、\(m_k\) は規則 \(r_k\) を構成する特徴量の数です。 全ての事例から特徴量の重要度を足し合わせることで、大域的な重要度を得ることができます。
\[J_j(X)=\sum_{i=1}^n{}J_j(x^{(i)})\]
事例の部分集合を選択して、そのグループの特徴量重要度を計算できます。
4.6.3 長所
RuleFitは特徴量間の相互作用を線形モデルに自動で追加します。 したがって、相互作用項を手動で追加する必要のある線形モデルの問題を解決し、非線形関係をモデリングする問題にも少し役立ちます。
RuleFit は分類問題と回帰問題の両方を扱えます。
作成される決定規則は二値であるため、規則が観測データに適用されるかどうかを調べることで簡単に解釈できます。 優れた解釈可能性は、決定規則内の条件の数が多すぎない場合にのみ保証されます。 個人的には、1〜3 個の条件の決定規則が合理的だと思います。 つまり、アンサンブルの木の最大の深さは 3 が良いということです。
たとえモデルに多くの決定規則がある場合でも、それらがすべての観測データに適用されるわけではありません。 個々の観測データにはほんのひと握りの決定規則のみ(= 非ゼロの重みを持つ)が適用されます。 これにより、個々のデータに対する解釈可能性が向上します。
RuleFitは便利な診断ツールを多数提供しています。 これらのツールはモデルに依存しないため、この本のモデル非依存 (model-agnostic) のセクションで紹介されています:特徴量重要度、partial dependence plots、特徴量の相互作用。
4.6.4 短所
RuleFit は、Lasso モデルにおいて非ゼロな重みを得るたくさんの規則を作り出すことがあります。 解釈性は特徴量の数が増えるにつれ低下します。 有望な解決策としては特徴量の影響を単調にすることです。 つまり、特徴量が増加すると、予測結果も増加する必要があるということです。
論文では度々 RuleFit の性能が、ランダムフォレストの予測性能に匹敵するほど良いと主張しています。 しかしながら、私が個人的に試したいくつかの場合において、がっかりするような性能でした。 まず、適用してみてどのような性能が出るかを確認しましょう。
RuleFit の手順をふんで得られる最終生成物は、追加の特徴(決定規則)を持つ線形モデルです。 しかし、線形モデルであるからこそ、重みの解釈が直感的ではありません。 通常の線形回帰モデルと同様に、"...他の全ての特徴量が固定されている場合に限る。"という"脚注"がついています。 また、規則が重複していると少し厄介になります。 例えば、自転車の数を予測するための1つの決定規則(特徴量)として "temp > 10" と "temp > 15 & weather='GOOD'" があるとします。 天気が良く、気温が15度以上であれば、自動的に気温が10度以上になります。 2つ目の規則が満たされているときに、1つ目の規則も満たされています。 2つ目の規則における推測された重みの解釈は"他の特徴量が固定され、天気が良く、気温が15度以上のとき、予測される自転車の数は \(\beta_2\) 増加する。"となります。 しかしここで、"他の特徴量が固定された場合"というのが問題になってきます。 なぜなら、2つ目の規則が適合しているとき、1つ目の規則にも適合し、解釈が意味の無いものになってしまうからです。
4.6.5 ソフトウェアと代替手法
RuleFit アルゴリズムは R では Fokkema と Christoffersen (2017)25 によって実装されています。 Python 実装は Github 上にもあります。
非常によく似たフレームワークは skope-rules という Python のモジュールでアンサンブルから規則を抽出します。 これは最終的な規則を学習する方法が違います。 まず、skope-rules はパフォーマンスのよくない規則を、recall(再現性)とprecision(適合率)に基づいて除去します。 そして、重複あるいは似ている規則が、論理項(変数 + 大なり/小なり)の多様性や F1-score に基づいて除去します。 最後に Lasso を用いる代わりに、out-of-bag の F1-score や規則を構成する論理項を用います。
Friedman, Jerome H, and Bogdan E Popescu. "Predictive learning via rule ensembles." The Annals of Applied Statistics. JSTOR, 916–54. (2008).↩
Fokkema, Marjolein, and Benjamin Christoffersen. "Pre: Prediction rule ensembles". https://CRAN.R-project.org/package=pre (2017).↩