6.4 Influential Instances
機械学習モデルは、学習データから生み出されたものであり、学習のインスタンス を1つ削除するとモデルの結果に影響が生じます。 学習データから削除するとモデルのパラメータや予測値を大幅に変化させるようなインスタンスのことを"影響力がある (influential)"と言います。 影響力のある学習インスタンスを特定することによって、機械学習モデルを"デバッグ"でき、モデルの振る舞いや予測をうまく説明できます。
この章では、影響力のあるインスタンスを特定するための2つのアプローチ、deletion diagnostics と影響関数 (influence functions)について説明します。 どちらのアプローチもロバスト統計に基づいており、外れ値やモデルの仮定のずれに頑健な推定方法です。
ロバスト統計は、データから予測モデルの重みや平均推定値のような、ロバストな推定量を得るための方法でもあります。 あなたの街にいる人々の平均収入を推定するため、通りすがりの10人にいくら稼いでいるか尋ねたい場合を考えてみましょう。
あなたが持つ標本が推定に全く適さない場合を除いて、あなたが平均収入を推定する際に1人から受ける影響はどの程度なのでしょうか。 この疑問に答えるには、個々の回答を省略することによって平均値を再計算する方法や、 どの程度平均値が影響を受けるかを、"影響関数"を用いて数学的に導出する方法が考えられます。
1つ目の手法である削除の方法(deletion approach)では、平均値を10回計算し直します。各回において 収入のデータの1つを省き、平均推定値がどの程度変化するかを測定します。 大きな変化は影響力の大きなインスタンスであることを意味します。
2つ目の手法は、統計量もしくはモデルの1次導関数の計算に対応した非常に小さな重みによって、ある人の収入を重み付けします。 この手法は"無限小解析 (infinitesimal approach)"や"影響関数 (influence function)"としても知られています。 ちなみに、平均値は単一の値に直線的にスケールするため、平均推定値は1つの回答に強く影響を受ける可能性があります。
よりロバストな選択肢は中央値です。なぜなら標本の中で1人だけ他の人の10倍稼いでいるような場合であっても、中央値は変化しないからです。
deletion diagnostics と影響関数は、機械学習モデルのパラメータや予測値に対して適用することで、それらの振る舞いをより良く理解したり、個々の予測値を説明することも出来ます。 影響力のあるインスタンスを見つけるための2つのアプローチを見る前に、外れ値と影響力のあるインスタンスとの違いについて説明します。
外れ値
外れ値とは、データセットの内の他のインスタンスから離れたインスタンスです。 "離れた"とは、他のすべてのインスタンスとの距離、ユークリッド距離などが非常に大きいことを意味します。 例えば、新生児のデータセットでは、体重が 6kg の新生児は外れ値とみなされます。 預金が多い銀行口座のデータセットでは、ローン専用口座(マイナス残高が大きく、取引が少ない)は外れ値と考えられます。 次の図は、1次元分布の外れ値を示しています。
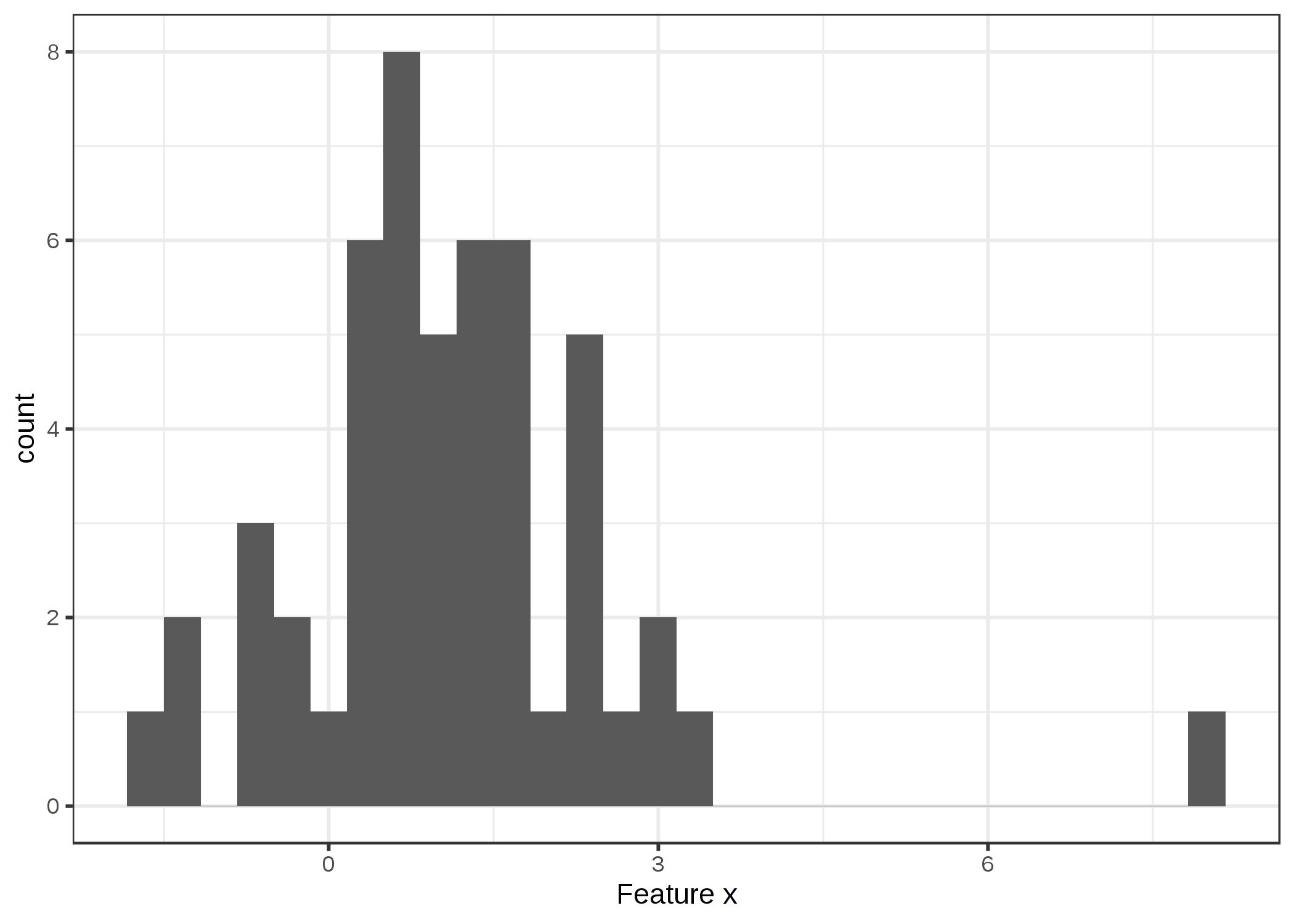
FIGURE 6.10: 特徴量 x は x=8 において外れ値を持つガウス分布に従う
外れ値は、興味深いデータ点になり得ます(例えば、criticism)。 外れ値がモデルに影響するとき、それは影響力のあるインスタンスとなります。
影響力のあるインスタンス (Influential instance)
影響力のあるインスタンスとは、削除すると学習されたモデルに強い影響を与えるインスタンスのことです。 学習データから特定のインスタンスを削除してモデルを再学習したときに、モデルのパラメータや予測値が変化するほど、そのインスタンスの影響力が大きくなります。 学習されたモデルにとってインスタンスが影響力を持つかどうかは、ターゲット y の値にも依存します。 次の図は、線形回帰モデルの影響力のあるインスタンスを示しています。
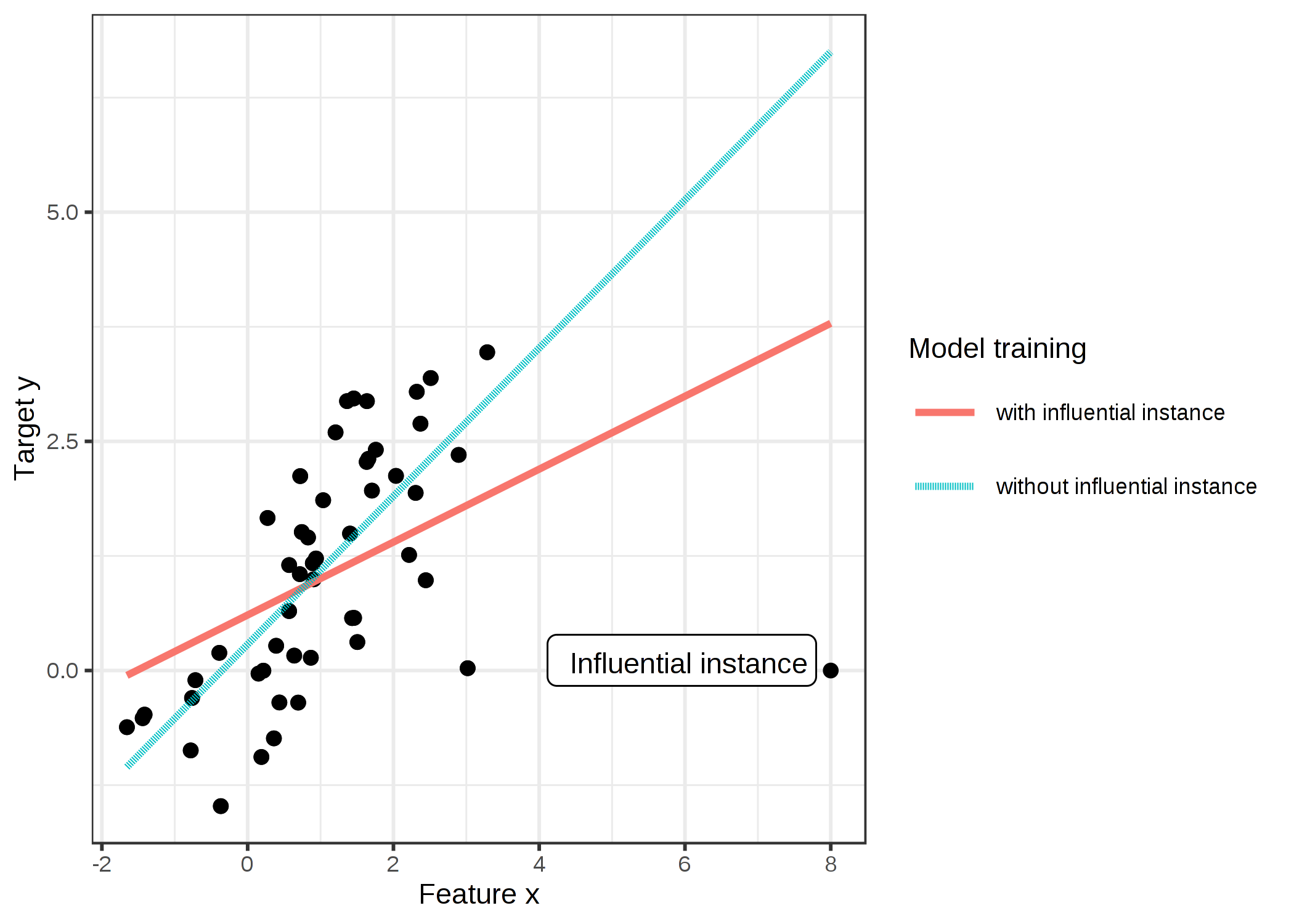
FIGURE 6.11: 特徴量が1つの線形モデル。一度は全てのデータで、もう一度は影響力のあるインスタンスを除いて学習されている。影響力のあるインスタンスを除くと、学習された傾き (重み、係数) が劇的に変化します。
影響力のあるインスタンスがモデルの理解に役立つ理由
解釈可能性において影響力のあるインスタンスの背後にある重要なアイデアは、モデルのパラメーターと予測を、学習データにまでさかのぼって追跡することです。学習器、つまり、機械学習モデルを生成するアルゴリズムは、特徴量 X とターゲット y からなる学習データを受け取って機械学習モデルを生成して返す関数です。例えば、決定木の学習器は、分割する特徴量と値を選択するアルゴリズムです。 ニューラルネットワークの学習器はバックプロパゲーションを用いて最適な重みを見つけます。
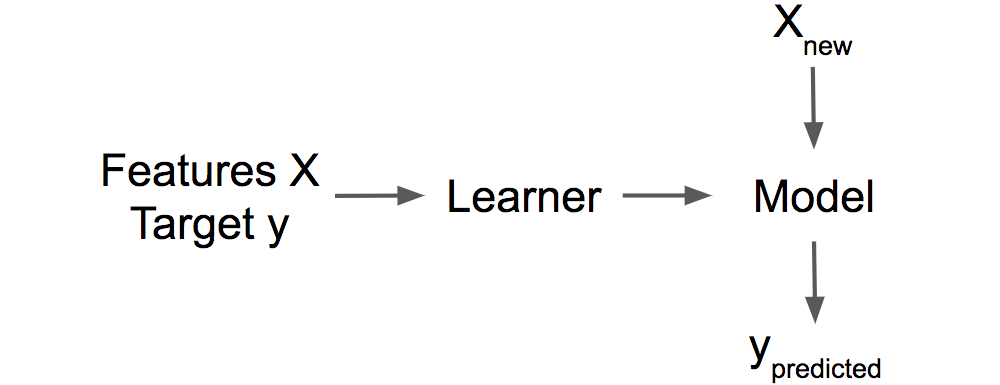
FIGURE 6.12: 学習器は学習データ(特徴量とターゲット)からモデルを学習する。学習されたモデルは新たなデータに対して予測を行う。
学習時にインスタンスを学習データから除いたら、モデルパラメータや予測はどの様に変化するのかを考えます。 これは、 部分依存プロット や 特徴量重要度 といった予測に用いるインスタンスの特徴量を操作したときに予測がどう変わるかを分析する他の解釈性へのアプローチとは対照的です。 影響力のあるインスタンスについては、モデルを固定されたものとして扱うのではなく、学習データの関数として扱います。 影響力のあるインスタンスは、大域的なモデルの振る舞いや、予測全般についての疑問に答える手助けをしてくれます。
どのように影響力のあるインスタンスを見つけるのでしょうか。 影響力を測るには2つの方法があります。 1つ目は、学習データからインスタンスを削除し、削減されたデータセットでモデルを再学習してモデルパラメータや (個別あるいはデータセット全体に対する) 予測の違いを観察することです。 2つ目は、モデルパラメータの勾配に基づいたパラメータの変化を近似することで、インスタンスの重みづけする方法です。 削除アプローチは理解が容易で、重みづけアプローチへの意欲を起こさせるため、前者から始めていきましょう。
6.4.1 Deletion Diagnostics
統計学者は影響力のあるインスタンスの領域、特に (一般化された) 線形回帰モデルでは多くの研究を既に行ってきました。 "影響力測定 (influential observations)"と調べると、最初の検索結果は DFBETA やクック距離 (Cook's distance) といった測定方法についてになるでしょう。 DFBETA は、インスタンスを削除した際のモデルパラメータへの影響を測ります。 クック距離 (Cook, 197763) はインスタンスを削除した際の予測への影響を測ります。 それぞれの測定のためには、毎回個別のインスタンスを除外しながらモデルを繰り返し再学習する必要があります。 全インスタンスでのモデルのパラメータや予測は、学習データからインスタンスを削除して得られたパラメータや予測と比較されます。
DFBETA は以下のように定義されます。
\[DFBETA_{i}=\beta-\beta^{(-i)}\]
ここで \(\beta\) はモデルが全データで学習された場合の重みベクトル、\(\beta^{(-i)}\) はインスタンス i を除いて学習された場合の重みベクトルです。 全く直感的と言っていいでしょう。 DFBETA は、ロジスティック回帰やニューラルネットワークのように重みパラメータを持つモデルにのみ有効で、決定木、アンサンブル、サポートベクタマシンなどには適用できません。 クック距離は線形回帰モデルのために考案され、一般化線形回帰モデルのための近似法が存在します。 学習インスタンスにおけるクック距離は、i 番目のインスタンスが学習時に除外されたときの、予測結果の差を2乗して(正規化された)総和をとったものとして定義されます。
\[D_i=\frac{\sum_{j=1}^n(\hat{y}_j-\hat{y}_{j}^{(-i)})^2}{p\cdot{}MSE}\]
ここで、分子は i 番目のインスタンスの有無によるモデルの予測結果の差の2乗をデータセット全体について総和したものです。 分母は特徴量の数 p に平均二乗誤差をかけたものです。 分母は全インスタンスにおいて同じであり、どのインスタンス i が除外されたかは問題ではありません。 クック距離は、学習時に i 番目のインスタンスを除外すると線形モデルの予測結果がどの程度変化するかを教えてくれます。
クック距離と DFBETA は、あらゆる機械学習モデルに適用できるのでしょうか。 DFBETA はモデルパラメータを要求するため、この測定方法はパラメータをもつモデルにしか使えません。 クック距離はモデルパラメータを要求しません。 面白いことにクック距離は線形モデルと一般化線形モデルの文脈外では普段見かけませんが、特定のインスタンスを除く前後でモデルの予測の差をとるというアイデアは非常に普遍的なものです。 クック距離の定義における問題点は MSE (平均二乗誤差)であることで、これは全てのタイプの予測モデルで意味があるとは限りません(例: 分類器)。
モデルの予測への影響における最も単純な影響力測定は、次のように書けます。
\[\text{Influence}^{(-i)}=\frac{1}{n}\sum_{j=1}^{n}\left|\hat{y}_j-\hat{y}_{j}^{(-i)}\right|\]
この表現は基本的にクック距離の分子ですが、違いは差の2乗の代わりに差の絶対値を使っていることです。 後の例で役立つため、私がそのように選択しました。 deletion diagnostic の一般形は、(予測結果のような)基準を選ぶことと、学習時にインスタンスを除いた場合と含む場合での基準の差を計算することで構成されます。
インスタンス j の予測について i 番目の学習インスタンスが与えた影響が何であったのかを説明するため、我々は簡単に影響を分解できます。
\[\text{Influence}_{j}^{(-i)}=\left|\hat{y}_j-\hat{y}_{j}^{(-i)}\right|\]
これはモデルのパラメータの差や損失の差に対しても有効でしょう。 次の例では、これらの単純な影響力測定を利用します。
Deletion diagnostics の例
以下の例では、子宮頸がんを与えられた危険因子から予測するためにサポートベクトルマシンを学習させ、どの学習インスタンスが最も全体に対して影響力を与えているのか、また、ある予測に対してどのインスタンスが最も影響を与えるのかについて測定しています。 がんの予測は分類問題であるため、がんの予測確率の違いを影響力として測定しています。 あるインスタンスをモデルの学習から取り除いた時、もし予測確率がそのデータセットの平均値から大きく増加(減少)する場合、そのインスタンスは影響力が強いインスタンスと言えます。 858 件の学習インスタンス全ての影響力を測定するためには、一度すべてのデータでモデルの学習し、インスタンスのうちの1つを取り除き再学習することを 858 回(=学習データの数)繰り返す必要があります。
最も影響力のあるインスタンスは約 0.01 の影響度を持っています。 0.01 の影響度は、もし 540 番目のインスタンスを取り除いた場合には予測確率が 1 %だけ平均値から変化することを意味しています。 この値は、癌の平均予測確率が 6.4 %であることを考慮するとかなり重要なものです。 可能な限りの全ての削除によって測定された影響度の平均値は 0.2 %です。 これでどの学習インスタンスがモデルに対して最も影響を与えたのかどうかが分かりました。 問題のあるインスタンスはないでしょうか。 測定に誤りはありませんか。 影響力のあるインスタンスは、それらに内包されるエラーがモデルの予測に対して強く影響を与えるため、エラーがないかどうか最初にチェックされるべきです。
モデルのデバッグとは別に、モデルをより良く理解するために何か知見を得ることは出来ないでしょうか。 ただ単に、最も影響力のある上位10個のインスタンスを表示するだけではあまり意味がありません。なぜなら、それらは多くの特徴量から構成されるインスタンスのただの表に過ぎないからです。 インスタンスを戻り値として返すメソッドは、それらをうまく表現する方法があるときにのみ有効です。 しかし、「影響力の無いインスタンスと影響力のあるインスタンスを差別化しているものはなにか」という問いを持つことで、どのような種類のインスタンスが影響力があるのかということをより良く理解できます。 この問いを回帰問題に落とし込み、インスタンスの影響度を、特徴量を入力とする関数としてモデリング出来ます。 "Interpretable Machine Learning Models" の章からどのようなモデルを自由に選択できます。 この例では、私は決定木(以下の図)を選びました。決定木によると、35歳以上の女性のデータがサポートベクトルマシンにとって最も影響力が有ることが示されています。 データセット中の、858 のうちの 153 の女性が 35 歳以上でした。 Partial Dependence Plots の章で、40歳を超えると急激にがんの予測確率が上昇する傾向が見られ、Feature Importance の章で、特徴量重要度として年齢が検出されていました。 影響力分析の結果、このモデルは年齢が高い部分でがんの予測が不安定になることを明らかにしています。 これは、それ自体が有益な情報です。 そして、これらのインスタンスに対する誤差がモデルに強い影響を持っていることを意味します。
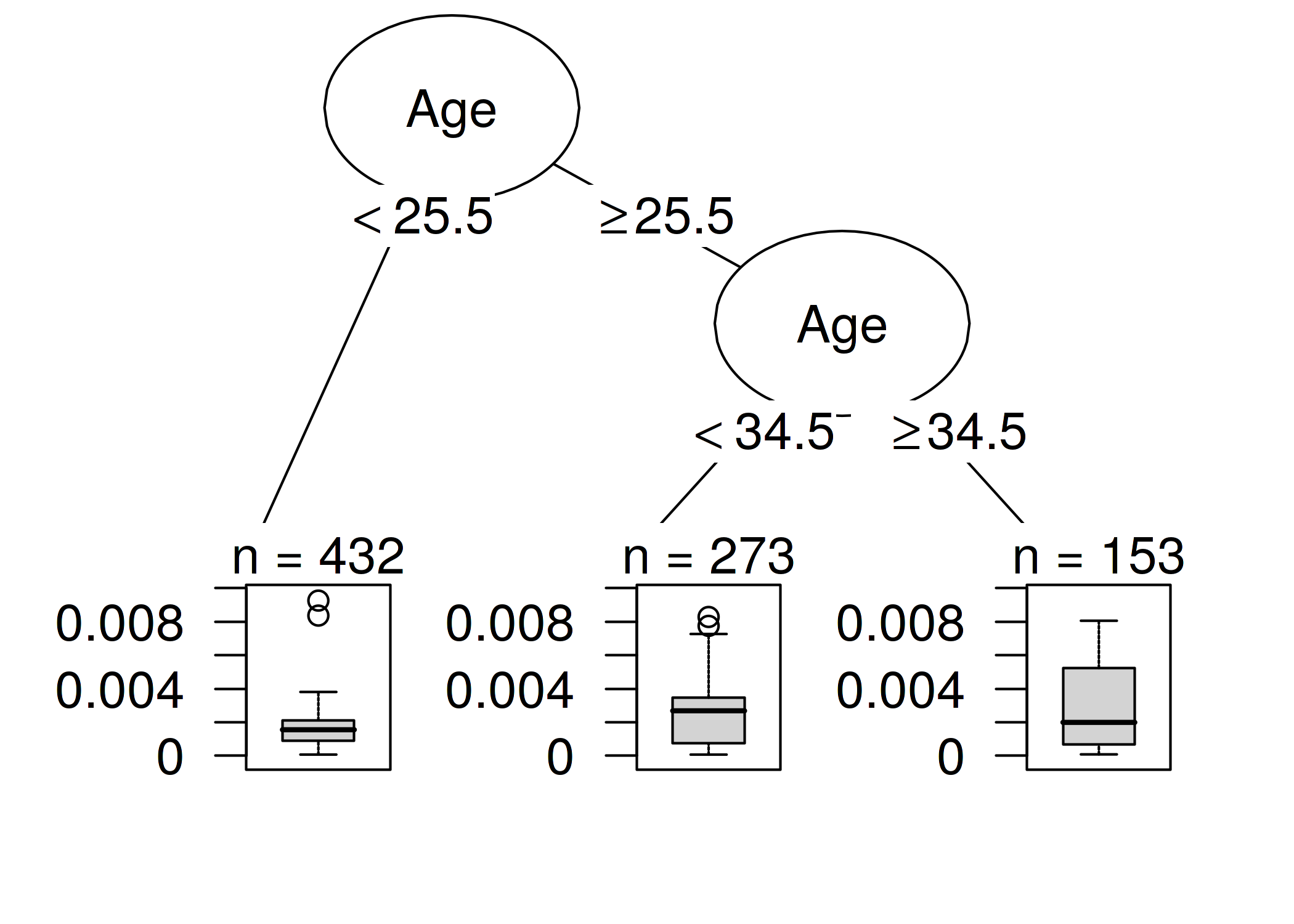
FIGURE 6.13: インスタンスの特徴量と影響力の関係の決定木モデル。木の最大深さは 2 に設定されている。
この最初の影響分析によって、全体で一番大きな影響力のあるインスタンスが明らかになりました。 ここでインスタンスの1つ、つまり 7 番目のインスタンスを選びます。 選んだインスタンスに対して、最も影響力のある学習データのインスタンスを見つけることで予測値を説明します。
これは、反事実的な質問です。 インスタンス i を学習のプロセスから除いた場合、7 番目のインスタンスに対する予測値はどのように変化するでしょうか。 全てのインスタンスに対してこの削除の処理を繰り返したとします。
次に 7 番目のインスタンスの予測値の中で最も大きな変化が生じた学習インスタンスを選びます。 この時選んだインスタンスは学習から削除し、インスタンスに対するモデルの予測値を説明するために用います。
7 番目のインスタンスは、がんの予測確率が最も高いインスタンス(7.35%) だったため、より深く分析するための面白い事例であると考え説明の対象として選びました。
例えば、 7 番目のインスタンスを予測するために影響力の最も強い上位 10 件を表形式で出力できます。 しかし、把握できない事もあるため、非常に便利というわけではありません。
繰り返しになりますが、影響力のあるインスタンスとそうでないインスタンスの特徴量を分析し、両者を区別するものを見つける方が、理にかなっています。 与えられた特徴量から影響度を予測するために決定木を学習しましたが、実際には、予測のためではなく、構造を発見するために使用されています。 次の決定木は、どの種類の学習インスタンスが 7 番目のインスタンスの予測に最も影響を与えたかを示しています。
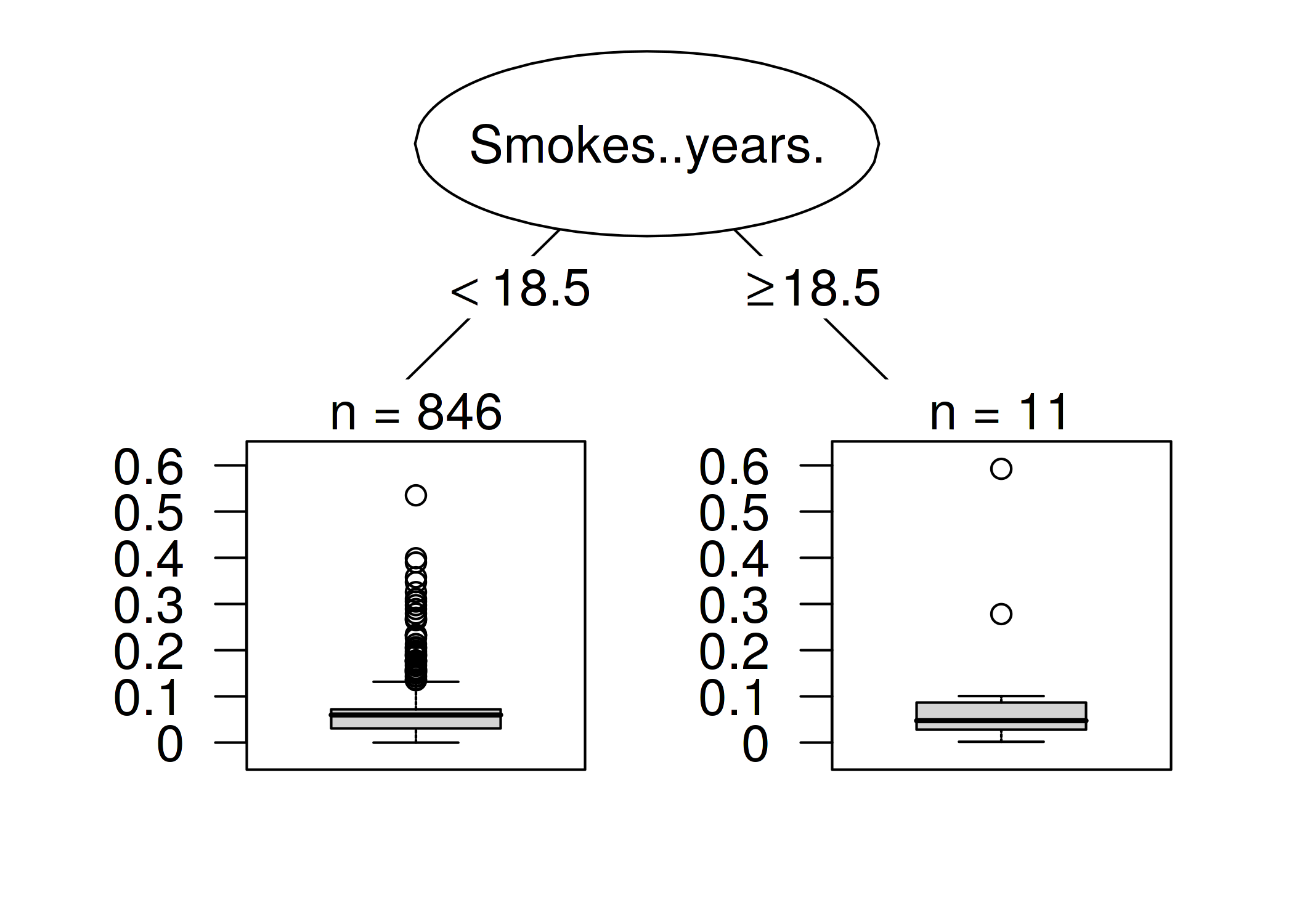
FIGURE 6.14: 7 番目のインスタンスの予測に最も影響を与えたインスタンスを説明する決定木。18.5年以上喫煙をする女性のデータは、7 番目のインスタンスの予測に対して大きな影響力を持ち、がんの確率を絶対値として平均 11.7 パーセント変化させる。
18.5年以上に渡って喫煙をしたことのある女性のインスタンスは,7 番目のインスタンスの予測に大きな影響を与えています。 7 番目のインスタンスに相当する女性は、34 年間の喫煙期間がありました。 データによると、12 人の女性 (1.40%) は、18.5年以上の喫煙期間がありました。 これらの女性の内1人でも喫煙期間に誤りがあった場合、7 番目のインスタンスに対する予測結果に大きな影響があります。
予測する上で最も極端な変化は、インスタンス 663 を削除した時に発生します。 患者が既に 22 年間喫煙していて、決定木による結果と一致していたとします。 インスタンス 663 を削除すると、7 番目のインスタンスに対する予測確率は、7.35% から 66.60% に変化します.。
最も影響力のあるインスタンスの特徴量を詳しく見ると、別の問題が見えてきます。 データによると、28才で22年間の喫煙経験を持つ女性がいるようです。 これは極端なケースであり、本当に6才で喫煙を始めたか、このデータが間違っているかのどちらかです。 私なら後者の可能性が高いと考えるでしょう。 まさにこれはデータの正確性について、疑問を持つべき状況です。
これらの例はモデルをデバッグするために、影響力のあるインスタンスを特定することがいかに有用であるかを示しています。 提案されたアプローチの問題点の1つは、学習インスタンスごとにモデルを再学習する必要があることです。 何千もの学習インスタンスがある場合、何千回と再学習しなければならないため、再学習全体が非常に遅くなる可能性があります。 モデルの学習に1日かかるとして、インスタンスが1000個あれば、影響力のあるインスタンスの計算には、並列計算なしなら約3年かかるでしょう。 誰もこんなことをする時間はありません。 この章の残りの部分では,再学習を必要としない方法を紹介します。
6.4.2 影響関数 (Influence Functions)
あなた: 学習インスタンスが特定の推論結果に与える影響を知りたいです。
研究者: その学習インスタンスを削除した上で、モデルを再学習し、推論結果の差を確認すればいいですよ。
あなた: いいですね!でも、再学習せずに測る方法は無いのですか?時間がかかりすぎちゃいますよ。
研究者: パラメータに対して二階微分可能な損失関数付きのモデルはありますか?
あなた: 私は logistic loss のニューラルネットワークを学習しました。つまり、答えは「はい」です。
研究者: とすると、インスタンスがモデルパラメータと予測値に与える影響を 影響関数 で測ることができます。 影響関数は、モデルパラメータまたは推論結果が学習インスタンスにどれだけ強く依存しているかを示す尺度です。 インスタンスを削除する代わりに、損失の中のインスタンスに非常に小さいステップで重み付けする方法です。 この方法では、勾配行列と Hessian 行列を用いて、現在のモデルパラメータ周辺の損失を近似します。 損失の重みを変える事は、インスタンスを削除することに似ています。
あなた: いいですね、これこそがまさに私が探していたものですよ!
Koh と Liang (2017)64 はインスタンスがモデルのパラメータや推論結果にどの程度影響するか測定するため、ロバスト統計学の手法の1つである影響関数を使うことを提案しました。 Delition diagnostics と同様に、影響関数は、モデル・パラメータと予測値から、影響のある学習インスタンスに遡ってトレースします。 ただし、学習インスタンスを削除するのに代わって、この方法では、インスタンスを経験的リスク(学習データに対する損失の合計)で重み付けしたときに、モデルがどの程度変化するかを近似しています。
影響関数の方法は、モデルパラメータに関する損失勾配を取得することを必要としますが、これは機械学習モデルの一部に対してのみ使用可能です。 ロジスティック回帰、ニューラルネットワーク、SVMでは使用可能ですが、ランダムフォレストのような決定木ベースの手法では使用できません。 また、影響関数は、モデルの動作の理解、モデルのデバッグ、データセットのエラー検出にも役立ちます。
ここでは、影響関数の直感的理解と数学的背景について説明します。
影響関数の数学的視点
影響関数の背後にある重要なアイデアは、学習インスタンスの損失を無限に小さいステップ \(\epsilon\) で重み付けすることであり、結果として新しいモデルパラメータが得られます。
\[\hat{\theta}_{\epsilon,z}=\arg\min_{\theta{}\in\Theta}(1-\epsilon)\frac{1}{n}\sum_{i=1}^n{}L(z_i,\theta)+\epsilon{}L(z,\theta)\]
ここで、\(\theta\) はモデルパラメータに関するベクトルであり、\(\hat{\theta}_{\epsilon,z}\) は非常に小さい数字である \(\epsilon\) で z を重み付けした後のパラメータベクトルです。 L はモデルで使用する損失関数、\(z_i\) は学習データ、 z は削除をシミュレートするために重み付けしたい学習インスタンスです。 学習データの、あるインスタンス \(z_i\) を少し(\(\epsilon\))アップウェイトして、他のインスタンスをダウンウェイトした場合、損失はどのくらい変わるのでしょうか。 この新しい2つが組み合わさった損失を最適化するために、パラメータベクトルはどのようになるでしょうか。 パラメータの影響関数、すなわち、学習インスタンス z をアップウェイトしたことによるパラメータへの影響は、以下のように計算できます。
\[I_{\text{up,params}}(z)=\left.\frac{d{}\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}=-H_{\hat{\theta}}^{-1}\nabla_{\theta}L(z,\hat{\theta})\]
最後の式 \(\nabla_{\theta}L(z,\hat{\theta})\) は、アップウェイトされた学習インスタンスのパラメータに対する損失勾配であり、勾配は学習インスタンスの損失の変化率です。 これは、モデルのパラメータ \(\hat{\theta}\) を少し変えると、損失がどれくらい変わるかを教えてくれます。
勾配ベクトルの正の項は、対応するモデルパラメータの小さな増加が損失を増加させることを意味し、負の項はパラメータの増加が損失を減少させることを意味します。 最初の部分 \(H^{-1}_{\hat{theta}}\) はヘシアン行列(モデルパラメータに対する損失の2次微分)の逆行列です。 ヘシアン行列は、勾配の変化率、すなわち損失と表現され、これは次のように計算されます。
\[H_{\theta}=\frac{1}{n}\sum_{i=1}^n\nabla^2_{\hat{\theta}}L(z_i,\hat{\theta})\]
くだけていうと、ヘシアン行列は、ある点で損失がどれだけ曲がっているかを記述しています。 ヘシアンは、"損失の曲率" を記述しており、曲率は見る方向に依存するため、単なるベクトルではなく行列です。 ヘシアン行列の実際の計算は、パラメータが多いと時間がかかります。 Koh と Liang は、効率的に計算するためのトリックを提案しています (この章ではサポートしていません)。 上式で説明したように、モデルパラメータを更新することは、推定されたモデルパラメータの周りで二次展開をした後に、ニュートン法を1回行うことと等価です。
この影響関数を直感的に理解するにはどうすればいいでしょうか。 この式は、パラメータ \(\hat{\theta}\) の周りに二次展開を形成することから来ています。 つまり、実際にはわからない、あるいは、インスタンス z の損失が削除、アップウェイトされたときにどのように変化するかを正確に計算することは複雑すぎるということです。 現在のモデルパラメータ設定における急峻度(=勾配)と曲率(=ヘシアン行列)の情報を用いて、関数を局所的に近似します。 この損失近似を使用して、インスタンス z をアップウェイトした場合の新しいパラメータがおおよそどのように見えるかを計算できます。
\[\hat{\theta}_{-z}\approx\hat{\theta}-\frac{1}{n}I_{\text{up,params}}(z)\]
近似されたパラメータベクトルは、基本的に元のパラメータから z の損失の勾配を引いたもの(損失を減らしたいので)を曲率(=逆ヘシアン行列を掛けたもの)でスケーリングされ、さらに 1/n でスケーリングされます。なぜなら、これは単一の学習インスタンスの重みであるためです。
次の図は、アップウエイトの仕組みを示しています。 x 軸は、\(\theta\) パラメータの値、y 軸は、アップウエイトされたインスタンス z の損失に対応する値を示しています。 ここでのモデルパラメータは簡単のために1次元としていますが、実際には高次元であることが多いです。 1/n だけ、インスタンス z の損失が改善される方向に移動します。 z を削除したときに損失が実際にどのように変化するかはわかりませんが、損失の1次微分と2次微分を用いて、現在のモデルパラメータの周りに、この2次近似を作成し、実際の損失がどのように振る舞うかを近似します。
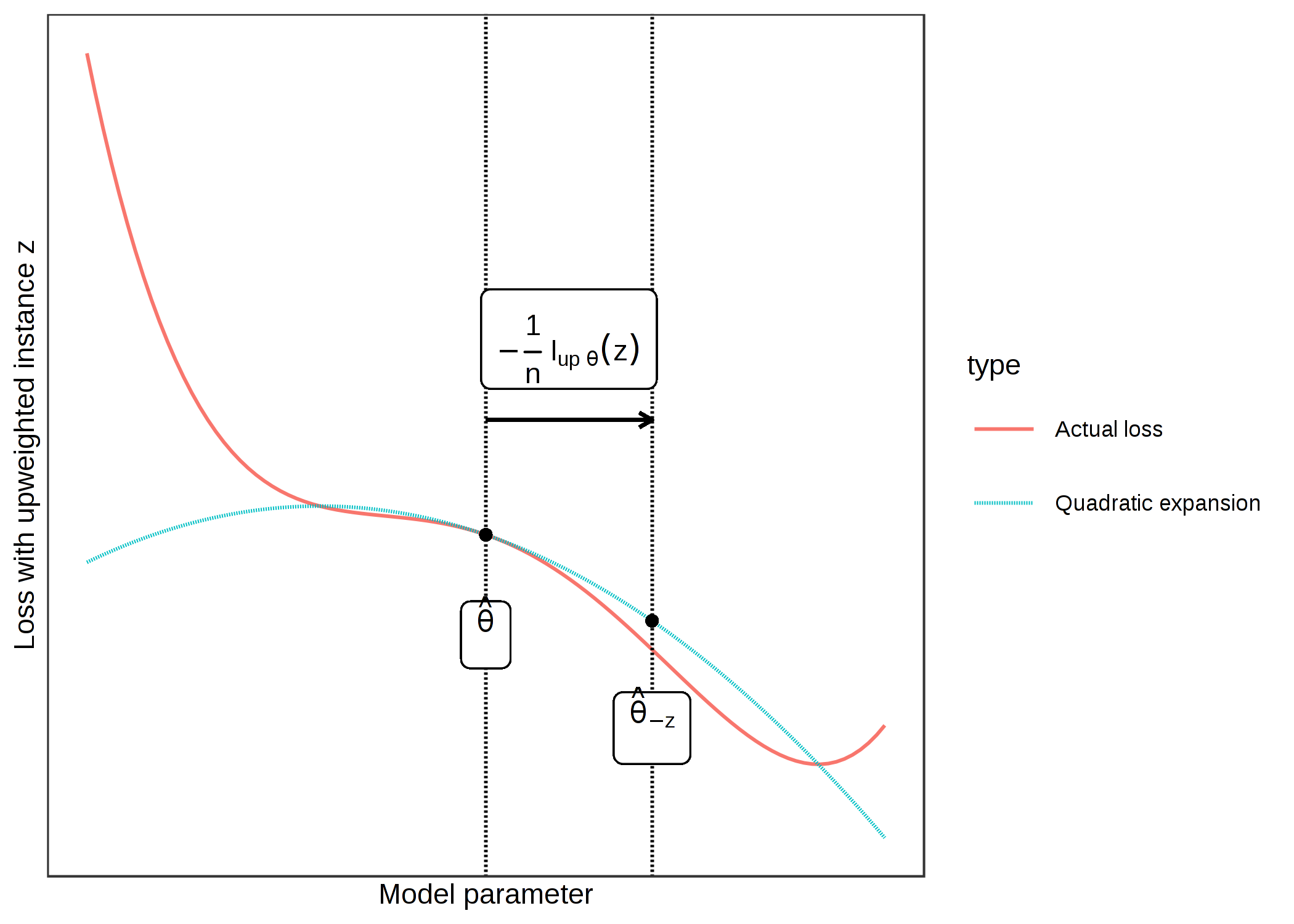
FIGURE 6.15: 現在のモデル・パラメータを中心とした損失の二次展開を形成してモデル・パラメータ(x軸)を更新し、1/n をアップウェイトされたインスタンス z での損失(y軸)が最も改善される方向に移動させます。この損失におけるインスタンスzに対してアップウェイトを行うことは、z を削除し、縮小されたデータでモデルを学習した場合のパラメータの変化を近似しています。
実際には新しいパラメータを計算する必要はありませんが、パラメータに対する z の影響度の指標として影響関数を使用できます。
学習インスタンス z をアップウェイトしたとき、 予測値はどのように変化するのでしょうか。 新しいパラメータを計算して、新たにパラメトライズモデルを用いて予測するか、あるいは、連鎖律を用いて影響度を計算できるので、予測に対するインスタンス z の影響度を直接計算できます。
\[\begin{align*}I_{up,loss}(z,z_{test})&=\left.\frac{d{}L(z_{test},\hat{\theta}_{\epsilon,z})}{d\epsilon}\right|_{\epsilon=0}\\&=\left.\nabla_{\theta}L(z_{test},\hat{\theta})^T\frac{d\hat{\theta}_{\epsilon,z}}{d\epsilon}\right|_{\epsilon=0}\\&=-\nabla_{\theta}L(z_{test},\hat{\theta})^T{}H^{-1}_{\theta}\nabla_{\theta}L(z,\hat{\theta})\end{align*}\]
この式の1行目は、ある予測 \(z_{test}\) に対する学習インスタンスの影響を、インスタンス z をアップウェイトして新しいパラメータを得たときのテストインスタンスの損失の変化として測定することを意味しています。 式の2行目については、導関数の連鎖律を適用して、パラメータに対するテストインスタンスの損失の導関数とパラメータに対する z の影響力の積を求めています。 3行目では、パラメータに対する影響関数に置き換えます。 3行目の第1項 \(\nabla_{\theta}L(z_{test},\hat{\theta})^T{}\) は、モデルパラメータに関するテストインスタンスの勾配です。
式を展開することは素晴らしいことであり、科学的かつ正確な方法で物事を示すことができます。 しかし、式の意味をある程度直感的に理解することはとても大切なことだと思います。 \(I_{\text{up,loss}}\) に対する式は、インスタンス \(z_{test}\) の予測に対する学習インスタンス z の影響関数は、"インスタンスがモデルパラメータの変化にどれだけ強く反応するか" に "インスタンス z をアップウェイトしたときにパラメータがどれだけ変化するか" を掛け合わせたものです。
この式のもう1つの見方として、影響力は、学習とテストの損失の勾配の大きさに比例します。 学習の損失の勾配が大きいほどパラメータへの影響が大きく、テストの予測への影響が大きいということになります。 テストの予測の勾配が大きいほど、テストインスタンスの影響力が大きくなります。 全体としては、学習インスタンスとテストインスタンスの間の類似性(モデルによって学習されたもの)の尺度としても見ることができます。
これが理論と直感的な解釈です。 次のセクションで、影響関数の適用方法について説明します。
影響関数の応用
影響関数には多くの応用例があり、いくつかは、この章で既に説明されています。
モデルの挙動の理解
異なる機械学習のモデルは、異なる手法で予測します。 もし、2つのモデルが同じ性能を持っていたとしても、それぞれのモデルが特徴量から予測する方法が異なっていると、別の場面では失敗する可能性があります。 影響力のあるインスタンスを明らかにし、モデルの特定の弱点を理解することは、機械学習モデルの動作の「メンタルモデル」を形成するのに役立ちます。
ドメイン不一致の対処 / モデルのデバック
ドメインの不一致を対処することは、モデルの挙動をより理解することと密接に関わっています。ドメインの不一致は学習データとテストデータの分布が異なっていることを意味し、これは、テストデータにおいて、モデルの精度低下を引き起こします。 影響関数は、エラーを引き起こした学習インスタンスを明らかにできます。 手術を受けた患者の結果を予測するモデルを学習したとします。 このとき、全ての患者は同じ病院の患者でした。 この学習されたモデルを、違う病院で試すと多くの患者に対してうまく動かないことが確認されました。 当然、2つの病院が異なる患者を持っていると考え、それぞれの病院のデータを見比べたとき、多くの特徴量が異なっていることがわかります。 しかし、モデルを壊した特徴量またはインスタンスは何なのでしょうか。 ここでもまた、影響関数が、問題に対する良い回答になります。 モデルが間違った予測を出した新しい患者の内の一人を取り出し、最も影響力の高いインスタンスを探し、分析します。 例えば、2番目の病院には平均的に高齢の患者が多く、学習データの中で最も影響力のあるインスタンスが最初の病院の少数の高齢患者であったとすると、単純に、モデルがこのサブグループを適切に予測するための学習データが不足していることがわかります。 モデルを2番目の病院でもうまく動かすためには、より多くの高齢の患者のデータで学習する必要があるという結論が得られるでしょう。
学習データを修正する
正しさを確認できる学習データの数に限りがある場合、どのように効果的な選択すると良いでしょうか。 最善の方法は、最も影響力のあるインスタンスを選択することです。なぜなら、定義より、それらが最もモデルに影響を与えるからです。 もし、明らかに間違った値を持つインスタンスがあったとしても、インスタンスに影響力がなく、予測モデルのためのデータだけを欲している場合、影響力のあるインスタンスを確認することがより良い方法です。 例えば、患者が病院に残るべきか、それとも早期退院してもよいかを予測するモデルを学習します。 患者を間違った時期に退院させることは、悪い結果を招く恐れがあるため、モデルが頑健で正しい予測をすることを確認する必要があります。 患者の記録はまとまりのない物になることもあり、データの質に完全な自信はありません。 しかし、患者のデータを確認し直すことは、とても時間がかかります。なぜなら、ある患者を再確認するには、病院は保管庫に眠る手書きの記録を調べるために、実際に誰かを派遣する必要があるからです。 患者のデータを確認するには1時間か、それ以上の時間がかかることがあります。 これらの費用を抑えるために、少数の重要なインスタンスを確認する方が合理的です。 最良の方法は、予測モデルに高い影響を与えた患者を選ぶことです。 Koh と Liang (2017)らは、この種類の選択が、ランダムな選択、損失が最も大きい患者、または間違った分類をされた患者を選ぶより遥かにうまく機能することを示しました。
6.4.3 長所
Deletion diagnostics と影響関数のアプローチは、 モデル非依存の章 で紹介されているほとんどの特徴量を摂動させるアプローチとは大きく異なります。影響力のあるインスタンスに注目すると、学習フェーズにおける学習データの役割が強調されます。 これによって、影響関数と deletion diagnostics は機械学習モデルに最適なデバッグツールの1つになります。 この本に紹介されている手法の中で、エラーに対してチェックすべきインスタンスはどれかを特定するのに直接役立つ唯一の方法です。
Deletion diagnostics はモデル非依存です。つまり、あらゆるモデルに対して適用可能です。 また、導関数に基づく影響関数は幅広いクラスのモデルに適用できます。
これらを使って様々な機械学習モデルを比較し、予測パフォーマンスを比較するだけでなく、モデルの様々な挙動をより深く理解できます。
この章ではこのトピックについては説明していませんが、導関数による影響関数は敵対的学習データを作るためにも使うことができます。 学習されたモデルが特定のテストインスタンスに対して正しく予測できないように操作されたインスタンスのことです。 敵対的な例の章 の方法との違いは、これらは学習時に行われるということです。これは poisoning attack として知られています。 興味のある方は、Koh and Liang (2017) の論文を読んでください。
Deletion diagnostics と影響関数については予測の差を、影響関数については損失の増加を考慮しました。 実際には、このアプローチは一般化可能であり、"インスタンス z を削除または重み付けを変えたときに、...はどうなりますか" というあらゆる質問に対応できます。 ここで、 "..." はモデルの任意の関数に入れ替えることができます。 例えば、ある学習インスタンスがモデルの全体的な損失にどれだけ影響するか、 ある学習インスタンスが特徴量重要度にどれだけ影響するか、または、ある学習インスタンスが決定木の学習時に最初の分割で選ばれる特徴量にどれだけ影響するかを分析できます。
6.4.4 短所
Deletion diagnostics は再学習が必要なため、非常に 計算コストがかかる方法 です。 ただ、歴史的にはコンピュータリソースは絶えず増加しています。 20年前には考えられたなかったような計算が、今ではスマートフォンで簡単に計算できます。 また、ノートパソコン上では数千の学習データを使って数百のパラメータを持ったモデルを数秒、もしくは数分で学習可能です。 従って deletion diagnostics が10年以内に大規模なニューラルネットワークでも機能すると想定することは、飛躍があるとは言い切れません。
影響関数は deletion diagnostics に代わる良い方法ですが、ニューラルネットワークのような微分可能なパラメータを持ったモデルにのみ適用可能です。 これらは、ランダムフォレスト、ブースティングツリー (boosted trees)、決定木のような決定木ベースの方法では使えません。 パラメータと損失関数を持つモデルであっても、損失を微分できない場合があります。 しかし、最後の問題にはトリックがあります。 たとえば、モデルが微分可能な損失の代わりに、例えば Hinge ロス を使用する場合、影響を計算するときに微分可能損失を代わりに使用します。 損失は、影響関数に対して問題のある損失を平滑化したものに置き換えられていますが、モデルは平滑化されていない損失で学習できます。
このアプローチはパラメータに対する二次展開を使用しているため、影響関数は近似にすぎません。 この近似は間違うかも知れず、実際に取り除いても、インスタンスへの影響が大きくなったり小さくなったりします。 Koh と Liang (2017) は影響関数によって計算された影響度が、実際にインスタンスを消去した後、再学習されたモデルから得た影響度と近い値だった例がいくつか示されています。 しかし、この近似が常に近いという保証はありません。
あるインスタンスが影響力があるかないか、判断するためのはっきりとした影響度の閾値は存在しません。 インスタンスを影響度でソートするのは便利ですが、単にソートするだけでなく、実際に影響力のあるインスタンスと影響力のないインスタンスを区別する手段があればもっと良いでしょう。 例えば、最も影響力のある10個のインスタンスを特定しても、例えばそのうちの上位3つだけが本当に影響力を持っているとすると、影響力がないものも含まれてしまいます。
影響度の測定は個々のインスタンスの削除のみを考慮し、複数のインスタンスの削除は考慮しません。 インスタンスのグループの効果によって、モデルの学習と予測に強く影響することがありえます。 しかし、問題は組み合わせ論にあります。 データから1つのインスタンスを削除するには \(n\) 通りの可能性があります。 データから2つのインスタンスを削除するには \(n(n-1)\) 通りの可能性があります。 データから3つのインスタンスを削除するには \(n(n-1)(n-2)\) 通りの可能性があります。 ここまで来たらもう分かると思いますが、組み合わせが多すぎます。
6.4.5 ソフトウェアと代替手法
Deletion diagnostics は非常に簡単に実装できます。 この章の例題のために書いたコードを見てください。(https://github.com/christophM/interpretable-ml-book/blob/master/manuscript/06.5-example-based-influence-fct.Rmd)
線形モデルや一般線形モデルでは、クック距離のような多くの influence 尺度が R パッケージの stats に実装されています。
Koh と Liang が論文から 影響関数の python コードを公開しています。 しかし残念ながら、それは論文のコードだけであり、保守性やドキュメントがない python モジュールです。 これは Tensorflow ライブラリ向けのコードであり、scikit learn などの他のフレームワークのブラックボックスモデルに直接使用できません。
Keita Kurita による 影響関数のブログ記事のおかげで、Koh と Liang の論文の理解が深まりました。 このブログ中では、ブラックボックスモデルの影響関数の背後にある数学的背景についてさらに深く掘り下げており、この手法を効率的に実装するための数学的な 'トリック' についても紹介されています。