5.5 Permutation Feature Importance

Permutation feature importance は、特徴量の値を並び替えることで、特徴量と真の結果との関係性を壊し、これによる予測誤差の増加を測定します。

5.5.1 理論

概念はとても単純です。 特徴量を並び替えたあとのモデルの予測誤差の影響を計算することで、特徴量の重要度を計算します。 特徴量の値を入れ替えるとモデル誤差が増加する場合、モデルは特徴量に依存した予測をしているので、その特徴量は「重要」です。 特徴量の値を入れ替えてもモデル誤差が変わらない場合、特徴量は「重要ではない」と言えます。 permutation feature importance は、Breiman (2001)34によってランダムフォレストのために導入されました。 この考えに基づいて、Fisher, Rudin, Dominici (2018)35は、モデルに依存しない特徴量重要度を提案し、これをモデル信頼度と呼んでいます。 彼らは、それに加えて特徴量の重要度に関する、より高度な考え方、例えば、多くの予測モデルがデータをうまく予測する可能性があることを考慮した（モデル固有の）バージョンも紹介しています。 彼らの論文 The permutation feature importance algorithm based on Fisher, Rudin, and Dominici (2018) は一読の価値があります。

入力: 学習モデル f, 特徴量行列 X, 目標ベクトル y, 誤差関数 L(y,f)

  1. 元のモデル誤差 eorig = L(y, f(X)) を推定します。（例: 平均二乗誤差）
  2. 各特徴量 j = 1,....,p について
    • データ X の特徴量 j を並べ替えて特徴量行列 Xperm を生成します。これにより、特徴量 j と真の結果 y との間の関連付けが解除されます。
    • 並べ替えられたデータの予測値に基づいて、誤差 eperm = L(Y,f(Xperm)) を推定します。
    • 並べ替えた特徴量の重要度 FIj= eperm/eorig を計算します。あるいは、差分 FIj = eperm - eorig も使用できます。
  3. FIが高い順に特徴量をソートします。

Fisher, Rudin, Dominici (2018)の論文では、特徴量 j を並べ替える代わりに、データセットを半分に分割し、それらの間で特徴量 j の値を入れ替えることを提案しています。 これは考えてみれば、特徴量 j を並べ替えるのと全く同じです。 より正確な推定をしたい場合は、各インスタンスを他のインスタンスの特徴量 j の値とペアにすることで、特徴量 j の並べ替えの誤差を推定できます（自分自身とのペアを除く）。 これにより、並べ替え誤差を推定するためのn(n-1)のサイズのデータセットが得られますが、膨大な計算時間がかかります。 厳密な推定値を得ることを真剣に考えている場合にのみ、この方法を使うことをお勧めします。

5.5.2 特徴量の重要度は、学習データとテストデータのどちらで計算するべきか

tl;dr: 明確な答えはありません。

学習データかテストデータかの疑問に答えることは、特徴量重要度とは何かという根本的な問題に首を突っ込むことになります。 学習データとテストデータに基づいた特徴量重要度の違いを理解するためには、「極端な」例が一番適しています。 50個のランダムな特徴量（200のインスタンス）に基づいて、連続でランダムなターゲットを予測するサポートベクタマシンを学習しました。 「ランダム」というのは、ターゲットが 50 個の特徴量とは独立であることを意味しています。 これは最新の宝くじの番号から明日の気温を予測するようなものです。 もしモデルが何かの関係性を「学習した」のならば、それは過学習だといえます。 そして実際、SVMは学習データに過学習してしまいました。 平均絶対誤差 (MAE) は学習データにおいて 0.29 、テストデータにおいて 0.82 であり、これは常に平均値が0 (MAEは 0.78 ) となる結果を予測するような最良のモデルの誤差でもあります。 言い換えれば、このSVMモデルは何の役にも立たないということです。 この過学習したSVMの50個の特徴量の重要度にどんな値が期待できるでしょうか。 まだ見ぬテストデータのパフォーマンスを向上させるような特徴量がないことから 0 となるのでしょうか。 もしくは、学習された関係性がまだ見ぬデータに一般化されているかどうかにかかわらず、重要度はモデルがどれだけそれぞれの特徴量に依存しているかを反映するのでしょうか。 学習データとテストデータの特徴量重要度の分布がどのように異なるのか見ていきましょう。

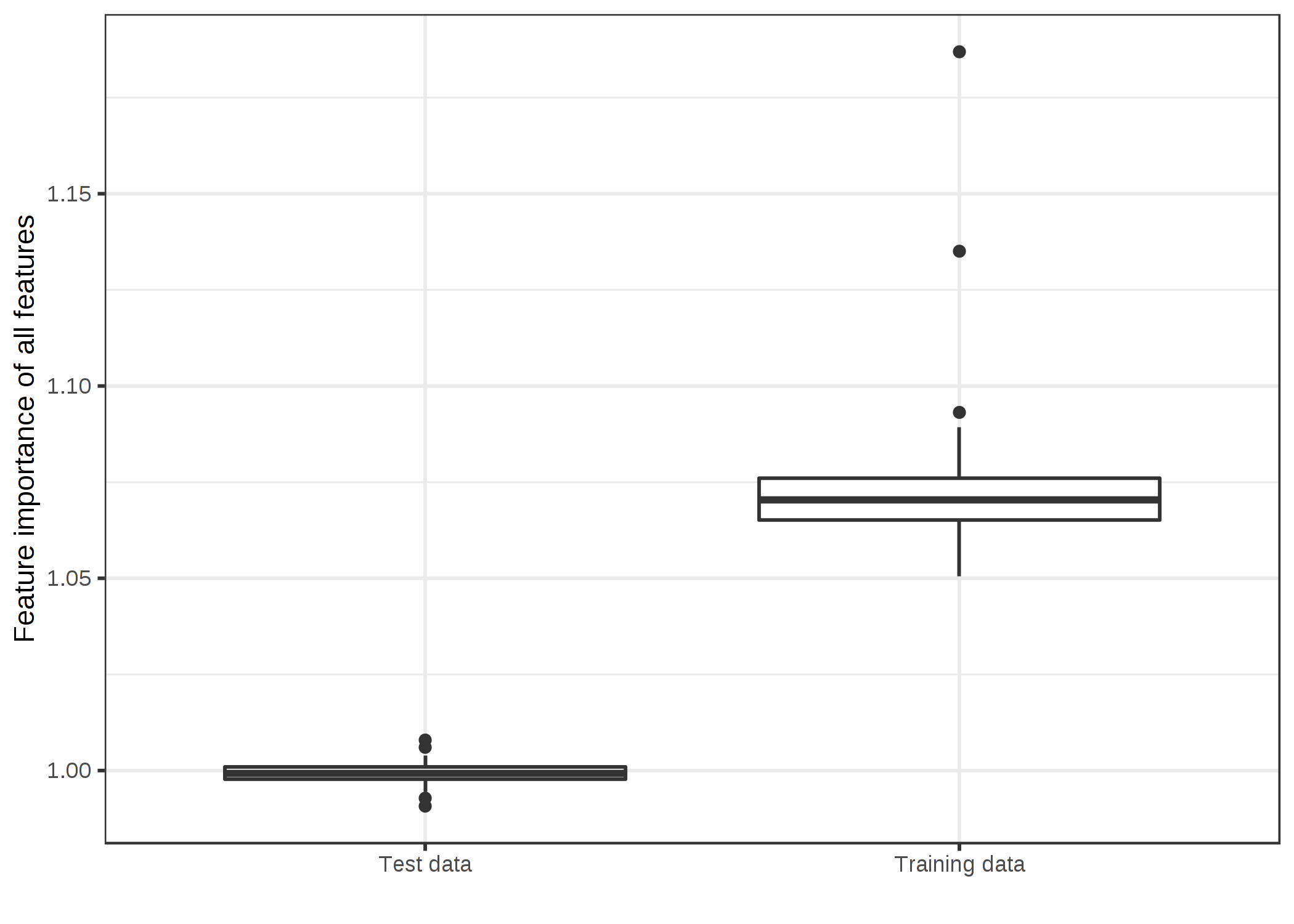
データのタイプによる特徴量重要度の分布。SVM は 50 個のランダムな特徴量を持つ 200 のインスタンスからなる回帰データセットで学習された。SVM は過学習しており、学習データに対する特徴量重要度では重要な特徴量がいくつか示されている。一方で、まだ見ぬテストデータに関して計算したところ、特徴量重要度は比率が 1 に近い値（＝重要ではない）となった。

FIGURE 5.26: データのタイプによる特徴量重要度の分布。SVM は 50 個のランダムな特徴量を持つ 200 のインスタンスからなる回帰データセットで学習された。SVM は過学習しており、学習データに対する特徴量重要度では重要な特徴量がいくつか示されている。一方で、まだ見ぬテストデータに関して計算したところ、特徴量重要度は比率が 1 に近い値（＝重要ではない）となった。

2つの結果のどちらが望ましいかは明確ではありません。 そこで、双方のケースそれぞれについて述べてみますので、どちらがいいのかあなた自身で考えてみてください。

テストデータのケース

こちらについては単純です。 学習データに基づくモデル誤差の推定値は役に立たないということから、特徴量の重要度はモデル誤差の推定値に基づいているため、学習データに基づく特徴量重要度は役に立たないと言えます。 これは機械学習において一番最初に学ぶことですが、モデルを学習したときと同じデータでモデル誤差（もしくは性能）を測ると、それは常に楽観的すぎるものになり、実際よりもモデルの性能がよく思えてしまいます。 したがって、permutation feature importance はモデル誤差に基づいているので、まだ見ぬテストデータを用いるべきと言えます。 学習データに基づく特徴量重要度では、実際にはモデルがただ過学習しているだけで全く重要でない特徴量にもかかわらず、予測に重要であるという誤解が生まれてしまいます。

学習データのケース

学習データを使用することに関する議論は形式化するのが難しいですが、私見ではテストデータに関する議論と同じくらい説得力があるように思えます。 違う観点からこの役に立たない SVM についてみていきましょう。 学習データによると、重要な特徴量は X42 でした。 X42 についての Partial Dependence Plot (PDP) について見ていきましょう。 PDP により、モデルの出力が特徴量の違いによってどのように変わるのかを見ることができ、これは汎化誤差に依存しません。 PDP では、学習データかテストデータかは問題ではないのです。

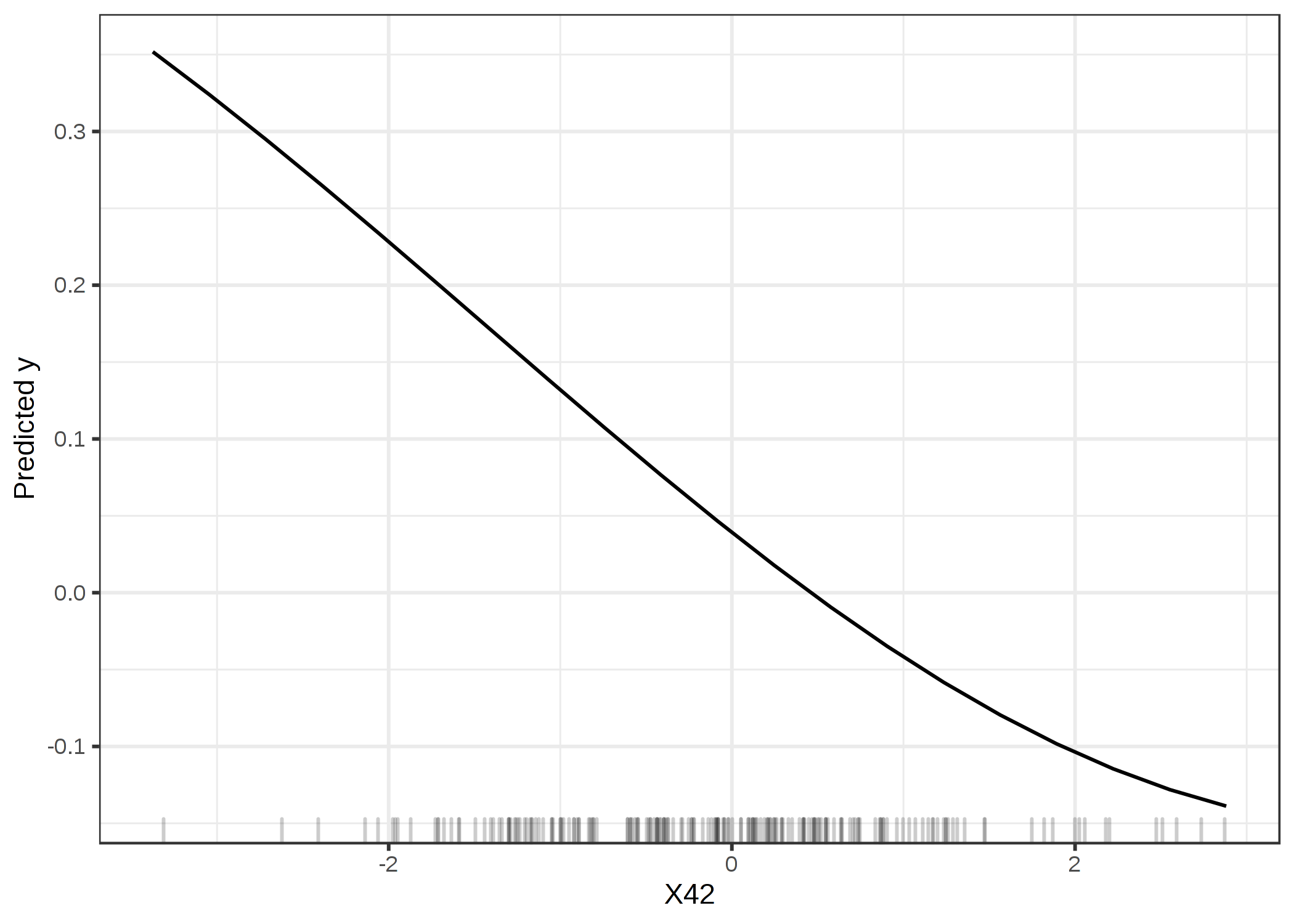
学習データに基づく最も重要な特徴量 X42 に関するPDP。このプロットによって、SVMが予測をする際にどのようにこの特徴量を用いているかが示されています。

FIGURE 5.27: 学習データに基づく最も重要な特徴量 X42 に関するPDP。このプロットによって、SVMが予測をする際にどのようにこの特徴量を用いているかが示されています。

このプロットによると明らかに SVM は特徴量X42 に依存して学習されていますが、テストデータに基づく特徴量重要度 (1) によると、この特徴量は重要ではありません。 学習データに基づく重要度は1.19であり、これはモデルがこの特徴量を用いるように学習されたことを示しています。 学習データに基づいた特徴量重要度は、予測をする際にそれらに依存しているという意味で、モデルにとって重要な特徴量はどれかを教えてくれます。

学習データを用いるケースの一環として、テストデータを使用することに対する反論を紹介したいと思います。 実際、最終的に可能な限り最良なモデルを得るために、すべてのデータを学習に使いたいと思うでしょう。 これは、特徴量重要度を計算するための未使用のテストデータが残されていないことを意味します。 モデルの汎化誤差を推定するときも同じような問題に直面します。 特徴量重要度を推定するために（ネストされた）交差検証を用いる場合、すべてのデータを学習に用いた最終的なモデルでは特徴量重要度が計算できず、一方でデータの一部を使ったモデルでは異なる振る舞いをしてしまうかもしれない、といった問題に直面するでしょう。

結局、モデルの予測がどの特徴量に頼っているのか（→学習データに基づく特徴量重要度）、もしくはどの特徴量がまだ見ぬデータに対するモデルの性能に寄与しているのか（→テストデータに基づく特徴量重要度）、どちらを知りたいのか決める必要があります。 私の知る限りでは、学習データとテストデータの疑問に関する研究はありません。 「役立たずの SVM」の例よりも徹底的な調査が必要でしょう。 より良い理解を得るためには、これらのツールについてより多くの研究と経験が必要になってくるでしょう。

次に、例をいくつか見ていきましょう。 重要度の計算は、どちらか1つを選ばなければならず、必要となるコードが少なくて済むので、学習データに基づいています。

5.5.3 例と解釈

分類と回帰の例を示します。

子宮頸がん（分類）

子宮頸がんを予測するためにランダムフォレストモデルを学習します。 誤差の増加を 1-AUC（1からROC曲線下面積を引いた値）で測定します。 並べ替えるとモデル誤差が 1 倍に増加する（＝変化なし）特徴量は、子宮頸がんの予測には重要ではありません。

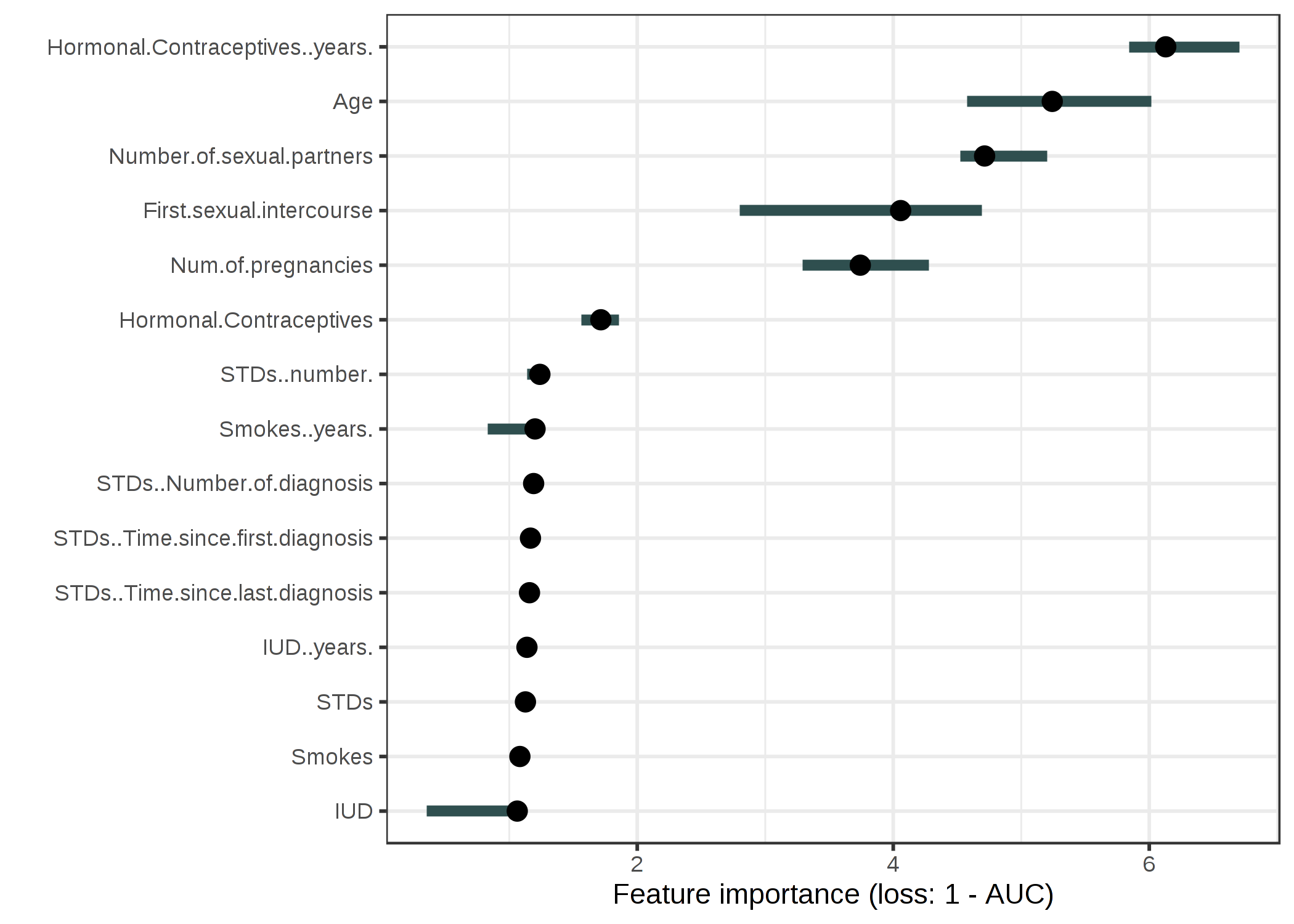
ランダムフォレストを用いて子宮頸がんを予測するための特徴量重要度。最も重要な特徴量は Hormonal.Contraceptives..years. で、1-AUCは 6.13 倍に増加した。

FIGURE 5.28: ランダムフォレストを用いて子宮頸がんを予測するための特徴量重要度。最も重要な特徴量は Hormonal.Contraceptives..years. で、1-AUCは 6.13 倍に増加した。

最も重要度の高い特徴量は Hormonal.Contraceptives..years. であり、誤差は 6.13 増加することがわかりました。

レンタル自転車（回帰）

SVM を用いて、気象条件とカレンダーの情報が与えられたときのレンタル自転車の台数を予測します。 誤差の測定には平均絶対誤差を使用します。

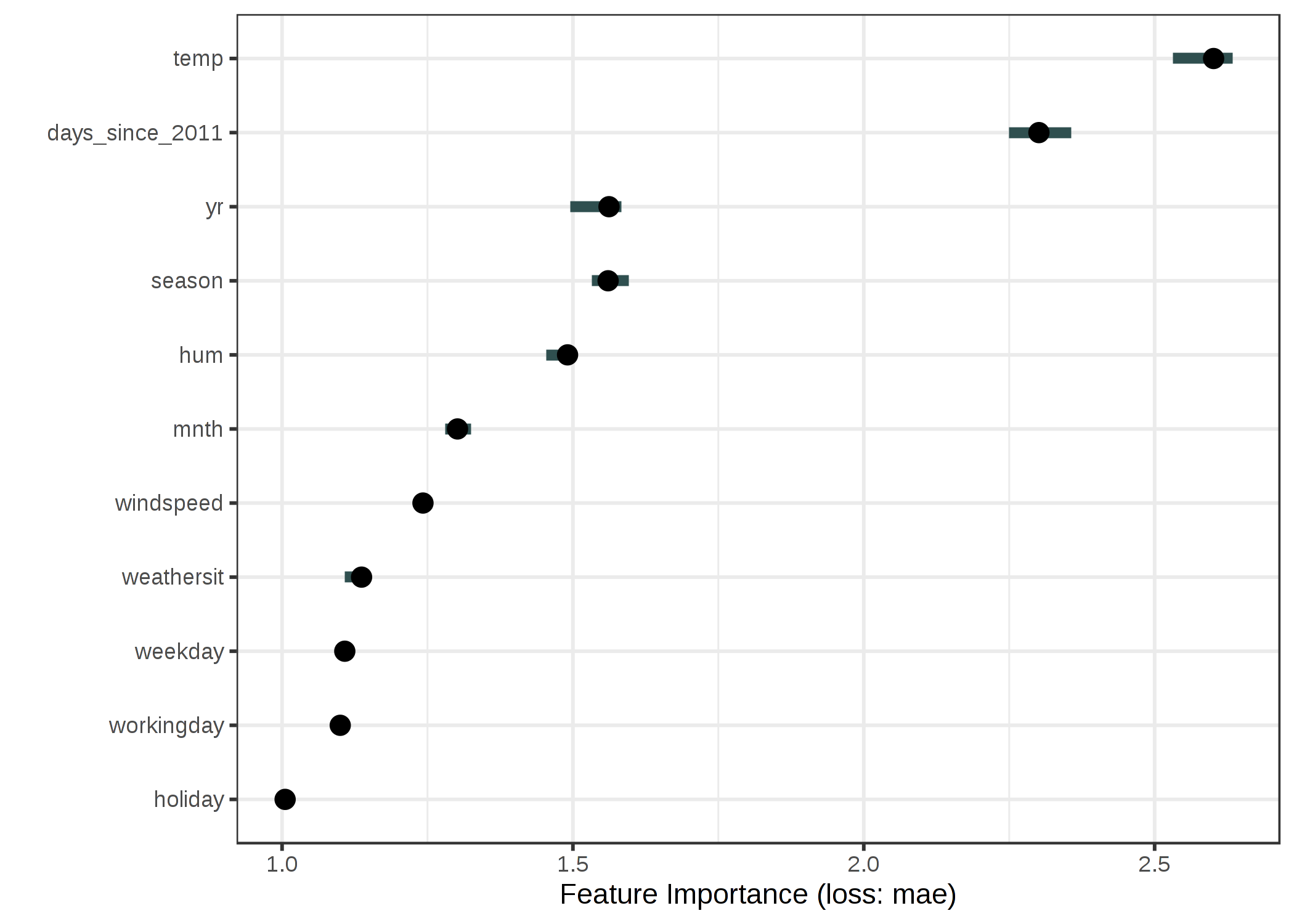
SVM を用いた自転車レンタル台数を予測したときの各特徴量の重要度。最も重要な特徴量は temp で、最も重要でない特徴量は holiday でした。

FIGURE 5.29: SVM を用いた自転車レンタル台数を予測したときの各特徴量の重要度。最も重要な特徴量は temp で、最も重要でない特徴量は holiday でした。

5.5.4 利点

特徴量重要度が高いということは、特徴量の情報が破壊されたときにモデル誤差が増加するという すばらしい解釈 が可能です。

特徴量重要度は、モデルの振る舞いについて 高度に圧縮されたグローバルな洞察 を提供します。

誤差の差分の代わりに誤差の比を使用することの良い側面は、特徴量重要度の測定値が異なる問題間で比較可能であることです。

重要度の計算は、自動的に他の特徴量とのすべての相互作用を考慮に入れます。 特徴量を並べ替えることは、他の特徴量との相互作用の効果も破壊します。 これは、並べ替えた特徴量の重要度が，モデル性能における特徴量としての主効果と相互作用による効果の両方を考慮に入れることを意味します。 このことは、2つの特徴量間の相互作用の重要度が、両方の特徴量の重要度測定に含まれているため、欠点でもあります。 これは、特徴量重要度が性能の全体的な低下の合計ではなく、総和が大きくなってしまうことを意味します。 線形モデルのように特徴間の相互作用がない場合にのみ、重要度はほぼ総和になります。

Permutation feature importance は モデルの再学習を必要としません。 他の方法の中には，特徴量を削除してモデルを再学習し、モデル誤差を比較するものもあります。 機械学習モデルの再学習には長い時間がかかるので、特徴量を並べ替える "だけ" で済めば多くの時間を節約できます。 特徴量の一部でモデルを再学習する方法は一見すると直感的に見えますが、データを減らしたモデルでは特徴量重要度に意味がありません。 我々が知りたいのは、モデルを固定して得られる特徴量重要度なのです。 削減されたデータセットで再学習すると、我々が興味を持っているモデルとは異なるモデルが得られます。 例えば、スパースな線形モデル（Lassoを使用）を、使用する特徴量の数を固定して重みを学習したとします。 データセットには 100 個の特徴量があり、非ゼロの重みの数を 5 に設定します。 非ゼロの重みを持つ特徴量のうちの 1 つの重要度を分析します。 次に、その特徴量を削除してモデルを再学習します。 その結果、同じように良い特徴量に非ゼロの重みが与えら、モデルの性能が変わらなかったとすると、先ほどの特徴量は重要ではないという結論に至ります。 また、こんなことも起こり得ます。 モデルは決定木で、最初の分割として選ばれた特徴量の重要度を分析します。 その特徴量を削除してモデルを再学習します。 別の特徴量が最初の分割として選択されるので、木全体が全く異なったものになります。つまり、（潜在的に）全く異なる木の誤差率を比較して、その特徴量が元の木にとって、どれだけ重要かを決定することになってしまうのです。

5.5.5 欠点

特徴量重要度を計算するために学習データを用いるべきか、テストデータを用いるべきかは明らかではありません。

Permutation feature importance は モデル誤差と関連しています 。 これは本質的に悪いことではありませんが、場合によっては我々が求めるものと異なります。 ある特徴量がモデルの性能に対しどういう意味を持つかを考えることなく、その特徴量によってモデルの出力がどう変わるかを知りたいケースもあります。 例えば、誰かによって特徴量が改ざんされた場合にモデルの出力がどの程度頑健か知りたい場合です。 この場合には、特徴量が並べ替えられた場合にどの程度モデルの性能が落ちるかではなく、モデルの出力の変化が各特徴量によってどの程度説明されるのかを知りたいはずです。 （特徴量によって説明される）モデルの出力変化と特徴量重要度は、モデルが良く汎化されている（つまり過学習していない）時には、強く相関します。

真の結果にアクセスできる必要があります。 もしモデルとラベル付けされていないデータのみが与えられ、真の結果がなかったならば、並べ替えた特徴量の重要度は計算できません。

permutation feature importance は特徴量のシャッフルに依存しているため、推定結果にランダム性を持ちます。 何度も計算すると、結果が大きく変わるかもしれません。 重要度の測定値を繰り返し平均すれば、推定結果は安定しますが、計算にかかる時間は増大します。

もし特徴量に相関があるのならば、permutation feature importance は現実的ではないインスタンスによって結果が歪められるかもしれません。 これは、Partial Dependence Plots と同じ問題です。 2つ以上の特徴量に相関がある場合、特徴量の並べ替えを行うことで、起こりえないデータを作り出してしまいます。 （人間の体重と身長のように）正の相関があり、その1つをシャッフルするとき、ありえないインスタンス（例えば身長 2m, 体重 30kg）を作り出してしまいますが、そのようなインスタンスも特徴量重要度の計算に使用されてしまいます。 言い換えれば、他の特徴量と相関のある場合の permutation feature importance は、特徴量の入れ替えによって得られた現実に観測しえないようなデータに対してモデルの性能がどの程度落ちたかについて考えていると言えます。 特徴量が強く相関しているかどうかをチェックし、相関がある場合は、特徴量重要度の解釈に注意するようにしましょう。

もう1つ、トリッキーなことがあります。 相関した特徴量を追加すると、両方の特徴量の間で重要度を分割することで、関連する特徴量の重要度が低下する、ということが起こり得ます。 特徴量重要度を「分割する」とはどういうことか、例を挙げてみましょう。 他の相関のない特徴量とともに前日の午前8時の気温を特徴量として使用し、降水確率を予測します。 ランダムフォレストで学習し、気温が最も重要な特徴量だとわかり、うまくいったので夜はよく眠れました。 では、午前8時の気温と強く相関するような午前9時の気温を追加したときを想像してみましょう。 午前8時の気温をすでに知っていたならば、午前9時の気温はそれほど多くの情報を与えません。 でも、特徴量はたくさんあるほうが良いはずです。 ランダムフォレストを2つの気温の特徴量と、他の相関のない特徴量から学習しました。 ランダムフォレストの個々の木は午前8時の気温を選んだり、午前9時の気温を選んだり、あるいは両方選んだりどちらも選ばなかったりしました。 2つの気温の特徴量のどちらもは、1つだけで学習したときよりも少しだけ重要度が高くなっていますが、特徴量を重要な順にリストかすると、どちらの気温も真ん中ぐらいの順位となっていました。 相関する特徴量を入れることによって、最も重要な特徴量をトップから平凡なものへと蹴り落してしまいました。 ある意味では、これは単に機械学習モデル（ここではランダムフォレスト）の動作を反映しているだけなので、問題ありません。 モデルが午前9時の気温にも頼ることができるようになったので、単純に午前8時の気温の重要度が低くなっただけです。 一方で、これによって特徴量重要度の解釈がかなり難しいものになってしまいます。 計測誤差について特徴量をチェックすることを想像してみてください。 チェックは大変なので、重要な特徴量を上位3つだけチェックすることに決めたとしましょう。 最初のケース(午前8時の気温のみ)では、最も重要な特徴量である気温をチェックしますが、2つ目のケース(午前9時の気温も含む) では、重要度がシェアされてしまっているので重要度の上位3つに気温の特徴量は1つも含まれません。 相関のある特徴量がある場合、重要度の値はモデルの動作レベルでは理解しうるものであったとしても、混乱を招く恐れがあります。

5.5.6 ソフトウェアと代替手法

例では、R パッケージの iml を用いました。 R パッケージ DALEX や vip、Pythonライブラリ alibi もまた、モデルに依存しない、permutation feature importance の実装があります。

PIMP と呼ばれるアルゴリズムは、重要度の p値 を提供するために、特徴量重要度アルゴリズムを改良しています。

  1. Breiman, Leo.“Random Forests.” Machine Learning 45 (1). Springer: 5-32 (2001).↩

  2. Fisher, Aaron, Cynthia Rudin, and Francesca Dominici. “Model Class Reliance: Variable importance measures for any machine learning model class, from the ‘Rashomon’ perspective.” http://arxiv.org/abs/1801.01489 (2018).↩