5.10 SHAP (SHapley Additive exPlanations)
This chapter is currently only available in this web version. ebook and print will follow.
Lundberg and Lee (2016)46による SHAP (SHapley Additive exPlanations)は、個々の予測を説明する手法です。 SHAP はゲーム理論的に最適な シャープレイ値 に基づいています。
SHAP が シャープレイ値 中の一節ではなく単独の章となっている理由は2つあります。 1つ目は、SHAP の作者らは KernelSHAP を提案したことです。これはローカルサロゲートモデル(local surrogate models) から着想を得たカーネルベースのシャープレイ値の代替的な推定手法です。 そして、 彼らはツリーベースのモデルに対する効率的な推定手法である TreeSHAP を提案しました。 2つ目は、SHAP にはシャープレイ値の集合に基づいた多くの大域的解釈モデルが付随することです。 この章では新たな推定手法と大域的な解釈の両方を説明します。
シャープレイ値 と 局所的モデル(LIME) の章を先に読んでおくことをおすすめします。
5.10.1 定義
SHAP の目標は、それぞれの特徴量の予測への貢献度を計算することで、あるインスタンス x に対する予測を説明することです。 SHAP による説明では、協力ゲーム理論によるシャープレイ値を計算します。 インスタンスの特徴量の値は、協力するプレイヤーの一員として振る舞います。 シャープレイ値は、"報酬" (=予測) を特徴量間で公平に分配するにはどうしたら良いかを教えてくれます。 各プレイヤーは、例えば表形式データでは、個別の特徴量の値となります。 プレイヤーは特徴量の値の組の可能性もあります。 画像を説明する例では、画素はスーパーピクセルとしてグループ化され、予測はそれらの間で分配されるでしょう。 SHAP が生んだ革新の1つは、シャープレイ値による説明が、線形モデルのような特徴量の効果の総和として表されることです。 この観点は、LIMEとシャープレイ値を結びつけます。 SHAPは、説明を次のように記述します。
\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]
ここで、g は説明モデル、\(z'\in\{0,1\}^M\) は連合ベクトル、 M は連合サイズの最大値、そして \(\phi_j\in\mathbb{R}\) は特徴量 j についての特徴量の属性であり、シャープレイ値です。 私が "連合ベクトル" と呼んでいるものは、SHAP の論文では "simplified features" と呼ばれています。 この名前が選ばれたのは、例えば画像データでは、画像は画素レベルではなく、スーパーピクセルに集約されたレベルで表されるためであると私は考えています。 私は z が連合を表すものであると考えるのは有用であると信じています。 連合ベクトルにおいて、要素が 1 のとき対応する特徴量が "存在" することを意味し、0 は "不在" であることを表します。 あなたがシャープレイ値について知っているならば、これは馴染み深く感じるでしょう。 シャープレイ値を計算するために、いくつかの特徴量だけがゲームに参加 ("存在") し、その他は参加しない ("不在") としてシミュレーションします。 連合の線形モデルとする表現は、\(\phi\) を計算するためのトリックです。 興味があるインスタンス x に対し、連合ベクトル x' は全てが1であるベクトル、つまり、全ての特徴量が"存在"となります。 このとき、式は次のように単純になります。
\[g(x')=\phi_0+\sum_{j=1}^M\phi_j\]
この式はシャープレイ値での表記に似ています。 実際の推定については後ほど触れます。 推定の詳細の前に、まずは \(\phi\) の性質について紹介します。
シャープレイ値は効率性 (Efficiency)、対称性 (Symmetry)、ダミー性 (Dummy)、加法性 (Additivity) を満たす唯一の解決案です。 シャープレイ値を計算するため、SHAP もこれらの性質を満たします。 SHAPの論文では、SHAPの性質とシャープレイ値の性質間の食い違いに気づくでしょう。 SHAPは次の望ましい3つの性質を説明します。
1) 局所正確性 (Local accuracy)
\[f(x)=g(x')=\phi_0+\sum_{j=1}^M\phi_jx_j'\]
もし \(\phi_0=E_X(\hat{f}(x))\) と定義し、全ての \(x_j'\) を 1 とするとき、これは、シャープレイの効率性となります。 名前が異なり、連合ベクトルを使っているだけです。
\[f(x)=\phi_0+\sum_{j=1}^M\phi_jx_j'=E_X(\hat{f}(X))+\sum_{j=1}^M\phi_j\]
2)欠損 (Missingness)
\[x_j'=0\Rightarrow\phi_j=0\]
欠損は、欠損している特徴量の属性がゼロになることを意味しています。 \(x_j'\) は連合を指し、値が 0 のとき、特徴量が不在を示していることに注意してください。 連合の表記では、説明されるインスタンスの全ての特徴量 \(x_j'\) は 1 である必要があります。 0 の存在は、注目しているインスタンスの特徴量の値が欠損していることを意味します。 この性質は、"普通の"シャープレイ値の性質には含まれていません。 では、なぜこれがSHAPのために必要なのでしょうか。 Lundberg は"minor book-keeping property" と呼んでいます。 欠損している特徴量は、理論的に、 \(x_j'=0\) と掛け合わされるため、局所的な精度を損なうことなく、任意のシャープレイ値を持つ事ができます。 欠損の性質は、欠損している特徴量は 0 のシャープレイ値を持つようにします。 実際には、これは定数の特徴量にだけ関係します。
3) 一貫性 (Consistency)
\(f_x(z')=f(h_x(z'))\) と \(z_{\setminus{}j'}\) は \(z_j'=0\) を表すとします。 任意の2つのモデル f と f' に対して、任意の入力 \(z'\in\{0,1\}^M\) が、\[f_x'(z')-f_x'(z_{\setminus{}j}')\geq{}f_x(z')-f_x(z_{\setminus{}j}')\]を満たすならば、\[\phi_j(f',x)\geq\phi_j(f,x)\]が成り立ちます。
一貫性は、もし特徴量の値の周辺寄与が(他の特徴量に関わらず)増加または同じままモデルが変化すると、シャープレイ値もまた、増加または同じままになるということを言っています。 Lundberg と Leeの付録で説明されている通り、一貫性から線形性、ダミー性、対称性が導かれます。
5.10.2 KernelSHAP
KernelSHAP はインスタンス x の予測に対するそれぞれの特徴量の値の寄与を推定します。 KernelSHAP は以下の5つのステップで構成されています。
- 連合 \(z_k'\in\{0,1\}^M,\quad{}k\in\{1,\ldots,K\}\) (1 = 連合内に特徴量が存在する, 0 =特徴量が存在しない) をサンプリングする。
- 最初に、\(z_k'\) を元の特徴空間に変換し、モデル f: \(f(h_x(z_k'))\) を適用しそれぞれの \(z_k'\) を予測する。
- SHAP カーネルを使って各 \(z_k'\) の重みを計算する。
- 重み付きの線形モデルで学習する。
- シャープレイ値 \(\phi_k\) と 線形モデルの係数を返す。
0 と 1 の連鎖ができるまでコイントスを繰り返す事によってランダムな連合を作成できます。 例えば、(1,0,1,0) のベクトルは、1番目と3番目の特徴量の連合を意味します。 K 個のサンプルされた連合は線形モデルのためのデータセットになります。 回帰モデルの目標は連合に対する予測です。 このモデルは、バイナリの連合ベクトルに対して学習されていないため予測はできないと思うかもしれません。 特徴量の連合から有効なデータインスタンスを取得するため、関数 \(h_x(z')=z\) (ただし、\(h_x:\{0,1\}^M\rightarrow\mathbb{R}^p\)) が必要です。 関数 \(h_x\) は 1 を説明したいインスタンス x に対する値に割り当てます。 表形式のデータの場合、0 をサンプリングした他のインスタンスの値に割り当てます。 これは、"特徴量の値が不在"であるということと、"特徴量の値は、データからランダムで選ばれた特徴量で置き換えられる"ということが等価であることを意味しています。 表形式データの場合、以下の図は連合から特徴の値に変換する方法を可視化しています。
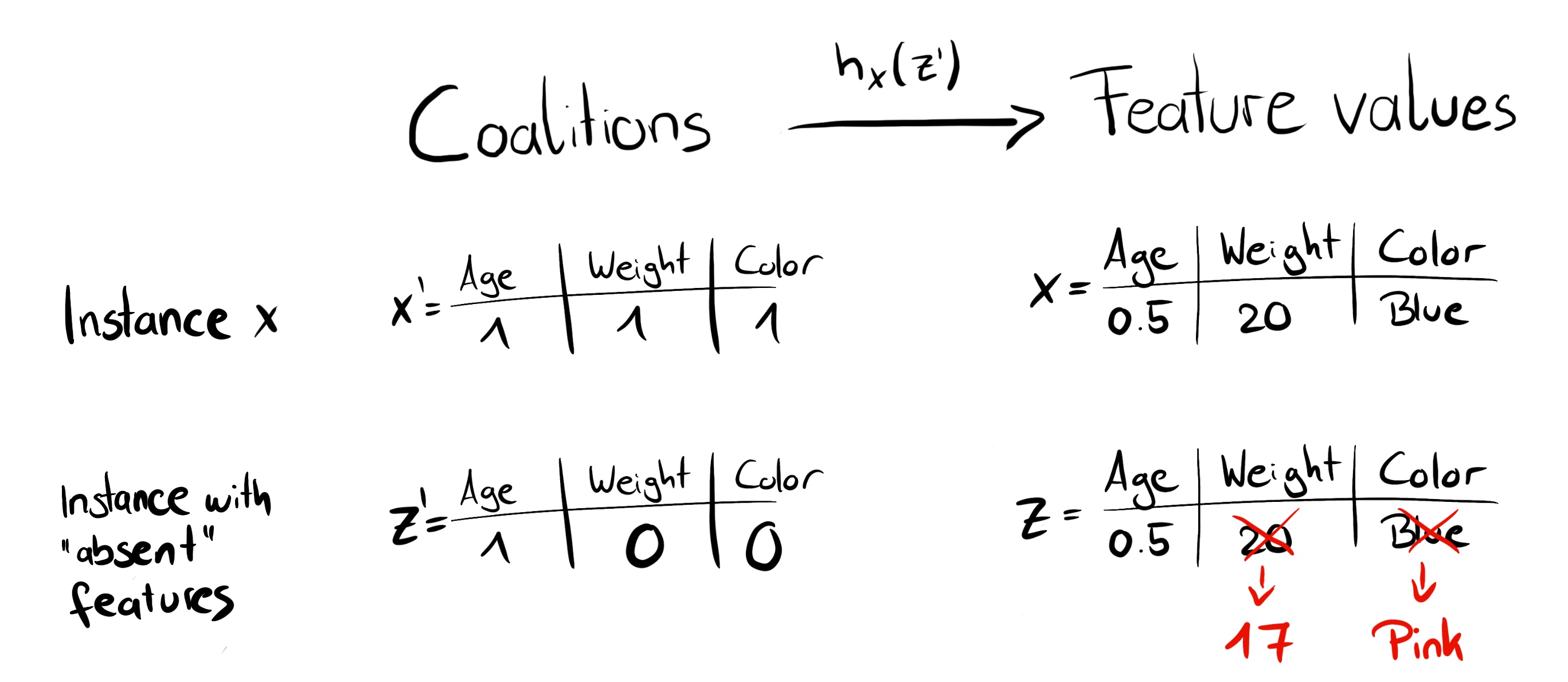
FIGURE 5.47: 関数 \(h_x\) は、連合から有効なインスタンスへの写像。特徴量が存在 (1) するとき、\(h_x\) は x の特徴量の値に変換する。特徴量が不在 (0) のとき、\(h_x\) はランダムにサンプリングされたデータインスタンスの値に変換する。
表形式データに対する \(h_x\) は、\(X_C\) と \(X_S\) は独立として扱い、周辺分布上で積分します。
\[f(h_x(z'))=E_{X_C}[f(x)]\]
周辺分布からのサンプリングは、存在する特徴量と存在しない特徴量の間の依存関係を無視することを意味します。 それゆえに、KernelSHAP は permutation ベースの解釈手法と同じ問題があります。 推定は、現実的に起こりそうもないインスタンスに過剰な重みを与えます。 結果は信頼できないものになります。 しかし、周辺分布からサンプリングすることは必要です。 もし、存在しない特徴量が条件付き分布からサンプルされた場合、結果の値はもはやシャープレイ値ではありません。 結果の値は、結果に寄与しない特徴量のシャープレイ値は 0 であるという、ダミーに関するシャープレイの公理に反します。
画像の場合、以下の図が、可能なマッピング関数を説明します。
FIGURE 5.48: 関数 \(h_x\) はスーパーピクセル(sp)の連合を画像にマッピングします。存在する特徴量(1)について、\(h_x\) は元の画像の相当する部分を返します。不在の特徴量(0)については、\(h_x\) は相当する部分をグレーアウトします。周りのピクセルの平均の色を割り当てるか似たような色で割り当てるかは任意です。
LIME との大きな違いは回帰モデルの中のインスタンスの重みです。 LIME は、元のインスタンスにどのくらい近いかによってインスタンスの重みを決定します。 連合ベクトルの中の 0 が多いほど、LIME の重みは小さくなります。 SHAP は、連合がシャープレイ値の推定で得るであろう重みに従って、サンプリングされたインスタンスに重み付けをします。 小さな連合(1が少ない)と大きな連合(1が多い)が最も大きな重みをとります。 この理由は以下の通りです。 もし個々の特徴量の影響を個別に調べることができるのであれば、個々の特徴量のほとんどを知ることになります。 もし連合が単一の特徴量で構成されている場合、予測に対する特徴量の個々の主な影響を知ることができます。 もし連合が1つを除いたすべての特徴量を基に構成されているなら、特徴量の全体効果(主要な効果+特徴量の相互作用)を知ることができます。 もし連合が特徴量の半分で構成されている場合、半分の特徴量となりうる連合が多くあるため、個々の特徴量についてほとんど知ることができません。 シャープレイ準拠の重みを達成するために、Lundbergらは、SHAP カーネルを提案しました。
\[\pi_{x}(z')=\frac{(M-1)}{\binom{M}{|z'|}|z'|(M-|z'|)}\]
ここで、M は連合の最大サイズ、 \(|z'|\) はインスタンス z' 内に存在する特徴量の数です。 Lundberg と Lee はこのカーネルの重みを使った線形回帰でシャープレイ値が得られることを示しています。 もし連合データにおいてSHAPカーネルをLIMEで使用する場合、LIMEもまたシャープレイ値を推定します。
連合のサンプリングに関してもう少し賢い方法があります。 最も小さい連合と大きい連合が重みのほとんどを奪います。 盲目的にサンプリングをする代わりに、サンプリング予算 K の一部使ってこれらの高い重みの連合を含めることで、よりよいシャープレイ値の推定を得ることができます。 そこで、1個 と Mー1個の特徴量を持つ可能な全ての連合(全部で 2M 個の連合)からスタートします。 十分な予算が残っている時(現在の予算は K - 2M)、2個の特徴量の連合や、M-2個の特徴量の連合などを含めます。 残りのサイズの連合からサンプリングを行い、重みを再調整します。
ターゲットと重みのデータを持っています。 重み付き線形回帰モデルを構築する全ては以下の通りです。
\[g(z')=\phi_0+\sum_{j=1}^M\phi_jz_j'\]
線形モデル g を損失関数 L を最適化することによって学習します。
\[L(f,g,\pi_{x})=\sum_{z'\in{}Z}[f(h_x(z'))-g(z')]^2\pi_{x}(z')\]
ただし、Z は学習用データです。 これは、線形モデルを最適化するための、古き良き、退屈な二乗誤差の合計です。 予測されたモデルの係数 \(\phi_j\) がシャープレイ値です。
線形回帰の設定なので、回帰のための標準ツールも使用できます。 例えば、正則化項を追加し、モデルをスパース化できます。 もし、私たちが損失 L に L1 ペナルティを追加することで、スパースな説明ができます。 (ただし、スパース化によって、有効なシャープレイ値のままであるかどうか確かでありません。)
5.10.3 TreeSHAP
Lundberg ら(2018)47 は、決定木やランダムフォレスト、GBT(gradient boosted trees)などといった木構造ベースの機械学習モデルのための SHAP のバリエーションとして、TreeSHAP を提案しました。 TreeSHAP は高速でモデルに特化した KernelSHAP の代替として導入されましたが、直感的でない 特徴量の属性を生成しうることが判明しました。
TreeSHAP は、周辺分布の期待値の代わりに条件付き期待値 \(E_{X_S|X_C}(f(x)|x_S)\) を使って関数の値を定義します。 条件付き期待値の問題点は、予測関数 f に影響を与えない特徴量が、非ゼロの TreeSHAP 推定値を取得しうることです。4849 非ゼロの推定値は、特徴量が実際に予測に影響する他の特徴量と相関を持つときに起こります。
TreeSHAPはどれほど高速なのでしょうか。 厳密なKernelSHAPと比較して、T を木の数、L を木の中の最大の葉の数、D を木の中の最大の深さとしたとき、計算量を \(O(TL2^M)\) から \(O(TLD^2)\) にまで削減できます。
TreeSHAPは影響を推定するために条件付き期待値 \(E_{X_S|X_C}(f(x)|x_S)\) を使用します。 あるインスタンス x と特徴量の部分集合 S に対して、1つの木の期待される予測値がどのように計算されるのか、直感的に理解してみましょう。 全ての特徴量で条件付けされているとき -- S は全ての特徴量の集合 -- 、期待される予測は、インスタンス x が含まれるノードの予測値になります。 どの特徴量でも条件付けされていないなら -- S は空集合 -- 、全ての終端ノードの予測の重み付き平均が期待される予測になります。 いくつかの特徴量を S が含んでいる場合(全てではない)、到達できないノードの予測は無視します。 ちなみに、到達できないとは、ノードへの決定経路(decision path)が、\(x_S\) の値と矛盾することを意味します。 残った終端ノードから、ノードサイズ(ノード内の学習サンプル数)によって重みづけられた予測値の平均を計算します。 この結果が S が与えられた時の x に対する期待される予測値となります。 問題点は、この手順をありうる特徴量の部分集合 S のそれぞれに対して適用しなければならないことです。
TreeSHAP は指数時間ではなく多項式時間で計算します。 基本的な考えは、全てのあり得る部分集合 S を同時に木へ押し込むことです。 それぞれの決定ノードに対し、部分集合の数を追跡する必要があります。 これは、親ノードの部分集合と特徴量の分割に依存します。 例えば、ある木における最初の分割が x3 とすると、全ての x3 を含む部分集合が1つのノード(xの行先)へ行きます。 x3 を含まない部分集合は、削減された重みと共に両方のノードへ行きます。 不運にも、異なるサイズの部分集合は異なる重みを持ちます。 アルゴリズムはそれぞれのノードにおける部分集合の重み全体を追跡しなければなりません。 これがアルゴリズムを複雑にしています。 TreeSHAP の詳細について、原論文を参照してください。 この計算は複数の木に対しても拡張されます。 シャープレイ値の加法性のおかげで、アンサンブル木のシャープレイ値は、個別の木のシャープレイ値の (加重) 平均となります。
次に、SHAP による説明を見てみましょう。
5.10.4 例
子宮頸がんのリスクを予測するために100の木を持つランダムフォレスト分類器を学習させました。 それぞれの予測を説明するために SHAP を使います。ランダムフォレストは木のアンサンブルであるため、Kernel SHAP の代わりに高速な TreeSHAP が使用できます。 しかし、この例では条件付き分布の代わりに周辺分布を用いています。これはパッケージで説明されており、元の論文では説明されていません。 Python の TreeSHAP 関数は周辺分布では低速ですが KernelSHAP よりは高速です、なぜならデータの行に比例して増加していくからです。
ここでは周辺分布を使っているので、説明はシャープレイ値の章と同じです。 しかし、Python の shap パッケージは異なる可視化になります。 特徴量の属性をシャープレイ値のような "力(forces)" として可視化できます。 それぞれの特徴量の値は予測値を増加させるか減少させるかの力を持ちます。 予測値は基準値から始まります。 シャープレイ値の基準値はすべての予測値の平均になります。 プロットでは、シャープレイ値は予測値を増加させる方向(正の値)か減少させる方向(負の値)を指す矢印となります。 この影響はデータインスタンスの実際の予測値で互いに釣り合っています。
次の図は、子宮頸がんデータセットからの2人の女性の SHAP による説明の様子を示しています。
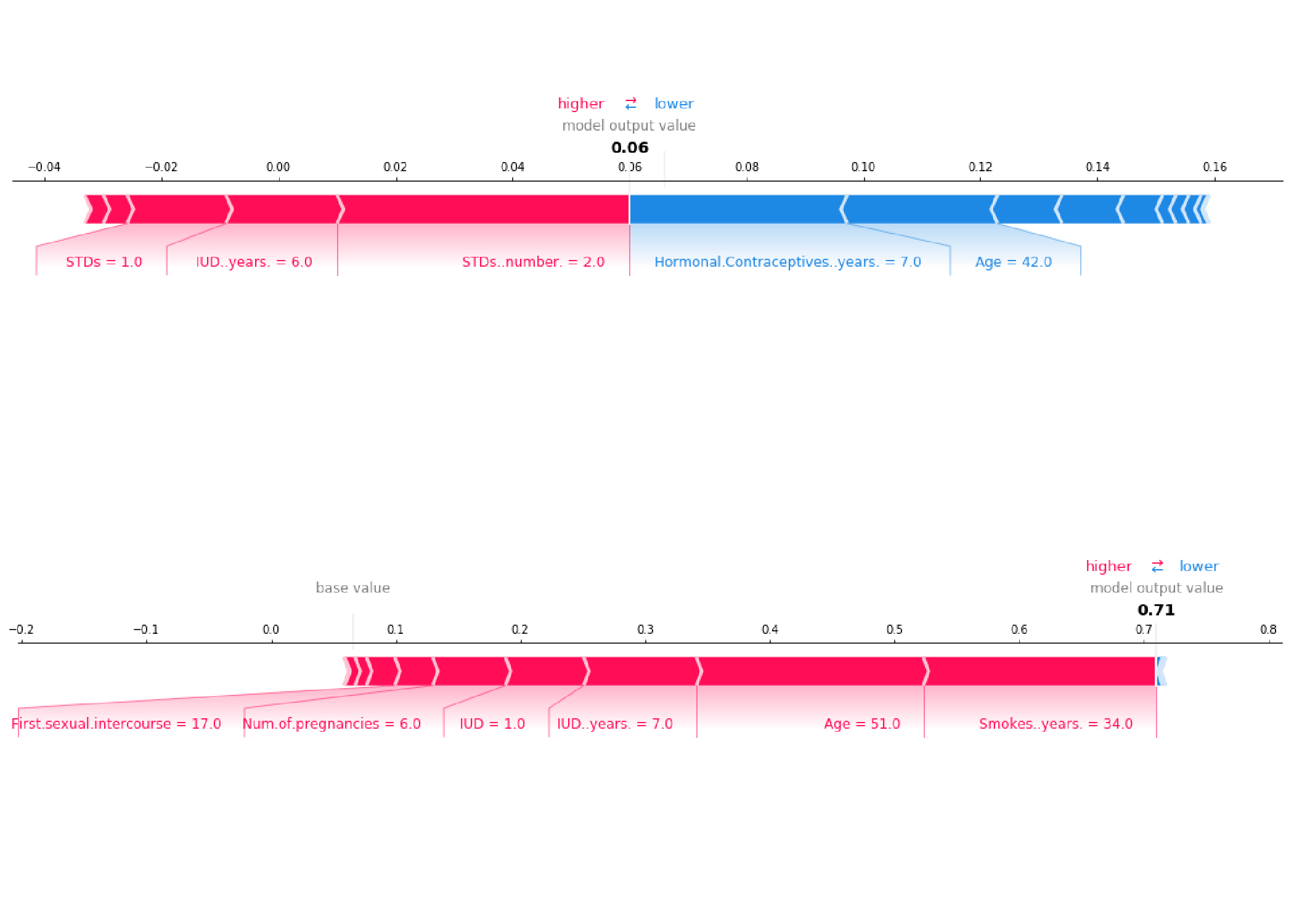
FIGURE 5.49: 2人の個人の予測される癌の確率を説明するためのSHAP。 ベースライン(平均予測確率)は 0.066 であり、 最初の女性の予測リスクは 0.06 と低くなっている。性感染症(STD)などのリスク増加効果は、年齢などの減少効果によって相殺される。2人目の女性の予測リスクは 0.71 と高くなっている。51歳と34年間の喫煙は、癌の予測リスクを高める。
これらは、個々の予測に対する説明でした。
シャープレイ値は、グローバルな説明のために組み合わせることができます。 すべてのインスタンスに対して SHAP を実行すると、シャープレイ値の行列が得られます。 この行列は、データインスタンスごとに1つの行があり、特徴量ごとに1つの列があります。 この行列のシャープレイ値を分析することで、モデル全体を解釈できます。
SHAPを使った特徴量重要度から始めます。
5.10.5 SHAP 特徴量重要度 (SHAP Feature Importance)
SHAP 特徴量重要度の背後にあるアイデアは単純です。 シャープレイ値の絶対値が大きい特徴量は重要です。 大域的な重要度を求めたいため、特徴量ごとのシャープレイ値の絶対値のデータ内での平均をとります。
\[I_j=\sum_{i=1}^n{}|\phi_j^{(i)}|\]
次に、重要度の降順に特徴量を並べ替え、それらをプロットします。 次の図は、以前子宮頸がんの予測のために学習したランダムフォレストの SHAP 特徴量重要度です。
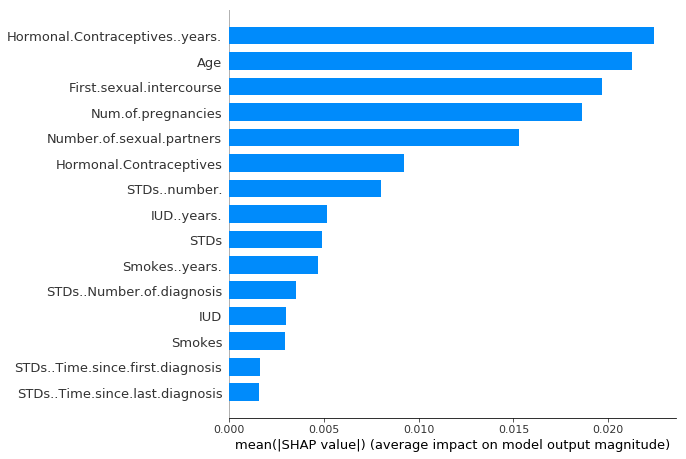
FIGURE 5.50: シャープレイ値の絶対値の平均として計算された SHAP 特徴量重要度。ホルモン避妊薬の使用年数は最も重要な特徴量であり、予測される癌の可能性の絶対値を2.4%変動させます (x軸での0.024).
SHAP 特徴量重要度は permutation feature importance の代替手法です。 ただし、これらの重要度の計測には大きな違いがあります。 Permutation feature importance はモデルの性能低下に基づきます。 一方で、SHAP は特徴量の帰属の大きさに基づいています。
特徴量重要度プロットは有用ですが、重要度以上の情報は含んでいません。 より有益なプロットとして、次の summary plot があります。
5.10.6 SHAP Summary Plot
この summary plot は、特徴量重要度と特徴量の影響を結びつけます。 Summary plot の各点はあるインスタンスの特徴量のシャープレイ値です。 y軸方向の位置は特徴量によって、x軸方向の位置はシャープレイ値によって決まります。 色は特徴量の値の大小を表します。 特徴量ごとのシャープレイ値の分布を知ることができるように、重複点はy軸方向にずらされています。 特徴量は重要度に従って並べられます。
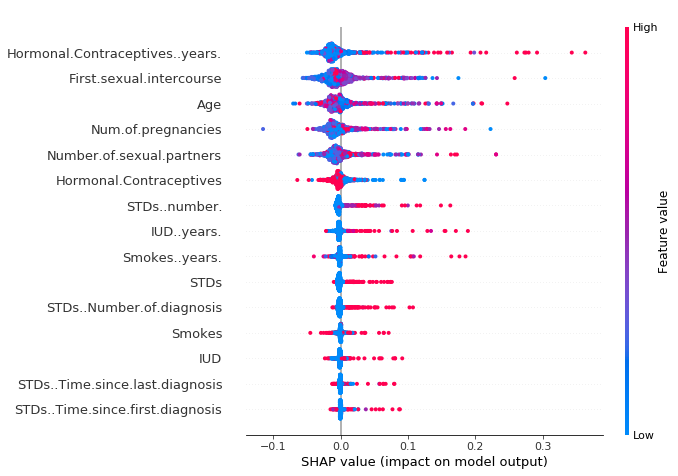
FIGURE 5.51: SHAP summary plot. ホルモン避妊薬使用年数が低いと予測される癌のリスクは低減し、高いとリスクが増加する。ただし、あらゆる効果はモデルの振る舞いを説明するものであり、必ずしも実世界での要因とは限らないことを注意。
Summary plotでは、特徴量の値と予測への重要度の関係性を示しています。 しかし、関係性の正確な姿を見るには、SHAP dependence plot を見る必要があります。
5.10.7 SHAP Dependence Plot
SHAP feature dependence は、最も単純な大域的な解釈のためのプロットかもしれません。 1) 特徴量を選ぶ。 2) それぞれのインスタンスに対して、x軸に特徴量の値を、y軸に対応するシャープレイ値をプロットします。 3) おわり。
数学的には、プロットは次の点を含みます。
\(\{(x_j^{(i)},\phi_j^{(i)})\}_{i=1}^n\)
ホルモン避妊薬使用年数の SHAP feature dependence を以下に示します。
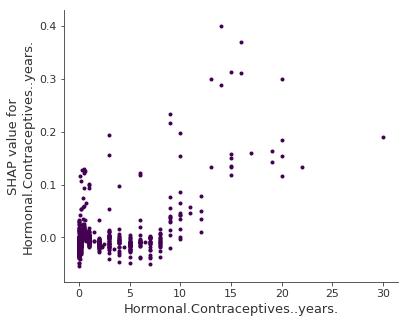
FIGURE 5.52: ホルモン避妊薬使用年数の SHAP feature dependence。 0年と比較して、低い年数のときは予測される確率を下げ、高い年数は予測される確率を増加させている。
SHAP dependence plot は、partial dependence plots や accumulated local effects の代替手法です。 PDP や ALE plot が平均効果を示すのに対して、SHAP dependence はy軸方向のばらつきも示せます。 特に相互作用がある場合には、SHAP dependence plot はy軸方向に更にばらつくでしょう。 SHAP dependence plot はそれらの特徴量の相互作用を強調表示することで、改善されます。
5.10.8 SHAP 相互作用値 (SHAP Interaction Values)
相互作用効果は、個々の特徴量の影響を考慮した後の追加の複合的な特徴量の効果です。 ゲーム理論から、シャープレイ相互作用は下記のように定義できます。
\[\phi_{i,j}=\sum_{S\subseteq\setminus\{i,j\}}\frac{|S|!(M-|S|-2)!}{2(M-1)!}\delta_{ij}(S)\]
\(i\neq{}j\) のときであり、\[\delta_{ij}(S)=f_x(S\cup\{i,j\})-f_x(S\cup\{i\})-f_x(S\cup\{j\})+f_x(S)\] です。
この方程式は特徴量の主効果を差し引くので、個々の効果を考慮した後の純粋な相互作用効果を得ることができます。 シャープレイ値の計算と同様に、私たちは、考えられる全ての特徴量連合 S の値を平均化します。 全ての特徴量のSHAP相互作用値を計算した時、インスタンスごとに、サイズが M x M の行列が得られます。ここで M は特徴量の数を表しています。
どのように相互作用インデックスを使用するのでしょうか? 例えば、相互作用の強さで自動的に SHAP feature dependence plot をつけます。
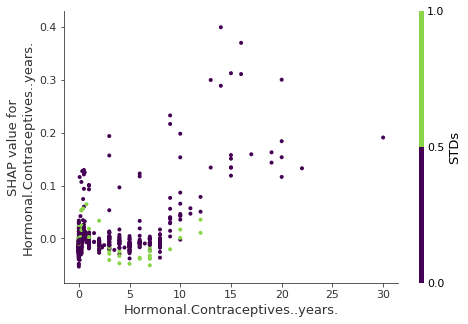
FIGURE 5.53: SHAP feature dependence plot による相互作用の可視化。ホルモン避妊薬の使用年数は性感染症と相互作用する。0年に近づく、STDの発生がある場合は予測される癌のリスクが増加する。避妊薬を数年に渡り使用した場合、STD の発生は予測されたリスクを減少させる。繰り返しになりなるが、これは、因果のモデルではない。この影響は交絡による可能性がある。(例えば、STDsと癌リスクの低下は、より多くの医師の診察と相関している可能性がある。
5.10.9 Clustering SHAP values
シャープレイ値を使って、データをクラスタリングできます。 クラスタリングの目的は似たようなインスタンスのグループをみつけることです。 クラスタリングは普通、特徴量を基に行われますが、特徴量が異なるスケールを持つことがよくあります。 例えば、身長はメートルで計測されていたり、色の強弱は 0 から 100 の数字であったり、センサー出力が -1 から 1 の間ということもあります。 そのような異なる比較できない特徴量を持つインスタンスの間の距離を計算することは困難です。
SHAP clustering は各インスタンスのシャープレイ値を使ってクラスタ化します。 これは、説明の類似性によってインスタンスをクラスタ化することを意味します。 全てのSHAP値は同じ単位 -- (予測空間の範囲) -- を持っています。 任意のクラスタ手法が使用可能です。 次の例では、階層的クラスタリングを使ってインスタンスを順序付けています。
プロットは多くの force plot で構成されており、それぞれがインスタンスの予測を説明します。 force plotを垂直に回転させ、クラスタリングの類似性にしたがって並べて配置しています。
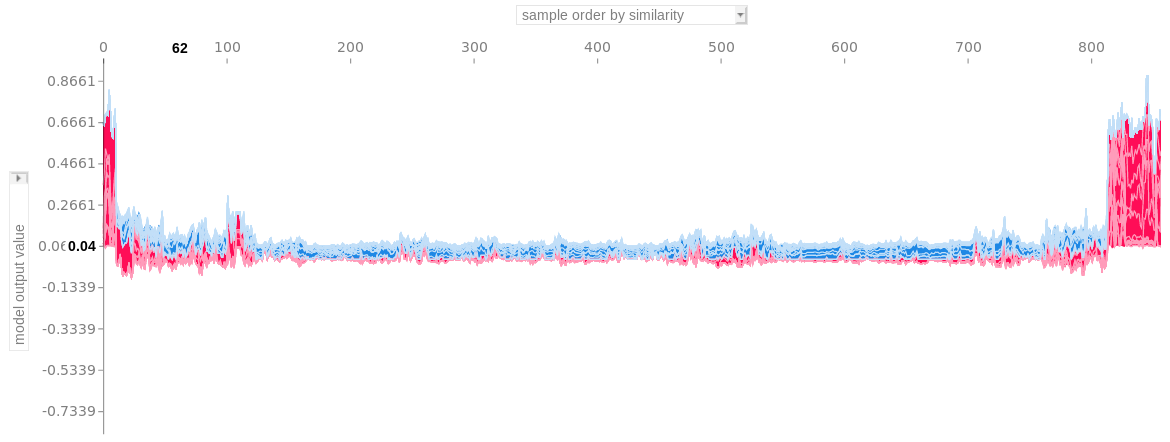
FIGURE 5.54: 説明の類似性によってクラスタリングされた Stacked SHAP explanations。それぞれのx軸の位置はデータのインスタンス。赤の SHAP 値は予測を増加させ、青の値は予測を減少させる。右にある目立つクラスタは、癌のリスクが高いと予測されたグループです。
5.10.10 長所
SHAPがシャープレイ値を計算する事から、シャープレイ値の全ての長所がSHAPにも反映されます。 SHAPは、ゲーム理論において "確かな理論的根拠" を持ちます。 予測は特徴量の中で公平に分配されています。 平均の予測と、個々の予測を比較することで 対照的な説明 ができます。
SHAPは、LIME と シャープレイ値をつなげます。 これは、両方の手法をより理解するためにとても有用です。 また、解釈可能な機械学習の分野を統一するために有用です。
SHAPは、決定木ベースのモデルに対して高速な実装を持っています。 私はこれが SHAP の人気の鍵だと信じています。 なぜなら、シャープレイ値の実装の一番の障害はその計算速度の遅さだからです。
早い計算速度は、大域的なモデルの解釈に必要な多くのシャープレイ値の計算をすることを可能にします。 大域的な解釈の手法は、特徴量重要度(feature importance)、feature dependence、interactions, clustering や summary plots があります。 SHAPを使用すると、シャープレイ値が大域的な解釈の "原子単位(atomic unit)" であるため、大域的な解釈と局所的な解釈が一致します。 もしあなたが LIME を局所的な説明に使い、partial dependence plot、permutation feature importance を大域的な説明のために使用した場合、共通の基盤が欠けています。
5.10.11 短所
KernelSHAPは計算に時間がかかります。 多くのインスタンスに対してシャープレイ値を計算したい時に、KernelSHAP は実用的ではありません。 また、SHAP feature importance などの、全ての大域的な SHAP の手法は多くのインスタンスのシャープレイ値を計算することを必要とします。
KernelSHAPは特徴量の依存関係を無視します。 ほとんどの他の permutation ベースの解釈手法も同じ問題を抱えています。 特徴量を、ランダムなインスタンスからの値に入れ替えることによって、簡単に周辺分布からのランダムサンプリングを実現できます。 しかしながら、もし、特徴量に依存がある場合(例えば、相関関係がある)、これは、ありそうもないデータ点に過剰な重みを与える事につながります。 TreeSHAP は、条件付きの予測を明示的にモデリングする事で、この問題を解決しています。
TreeSHAP は直感的ではない特徴量の属性を作り出す可能性があります。 TreeSHAP が現実的ではないデータ点を作り出してしまう問題を解決できる一方で、別の問題を作り出してしまいます。 TreeSHAP では、value function は条件付き期待予測に従うように変更されています。 そのため、予測に影響を与えない特徴量に対しても、TreeSHAP は非ゼロの値を持つ可能性があります。
シャープレイ値の欠点もまた、SHAPに適用されます。 シャープレイ値は誤解する恐れがあり、新しいデータに対してシャープレイ値を計算するためには、データにアクセスできる必要があります(TreeSHAPを除いて)。
Lundberg, Scott M., and Su-In Lee. "A unified approach to interpreting model predictions." Advances in Neural Information Processing Systems. 2017.↩
Lundberg, Scott M., Gabriel G. Erion, and Su-In Lee. "Consistent individualized feature attribution for tree ensembles." arXiv preprint arXiv:1802.03888 (2018).↩
Sundararajan, Mukund, and Amir Najmi. "The many Shapley values for model explanation." arXiv preprint arXiv:1908.08474 (2019).↩
Janzing, Dominik, Lenon Minorics, and Patrick Blöbaum. "Feature relevance quantification in explainable AI: A causality problem." arXiv preprint arXiv:1910.13413 (2019).↩