5.9 シャープレイ値 (Shapley Values)

予測は、インスタンスの特徴量の値が "プレイヤー"で、予測が報酬であるようなゲームを想定して説明できます。シャープレイ値（協力ゲーム理論の手法）は、特徴量の間で "報酬" を公平に分配する方法を教えてくれます。

5.9.1 一般的なアイデア

次のシナリオを想定してみましょう。

あなたは、アパートの価格を予測するための機械学習モデルを学習しました。あるアパートは €300,000 と予測されており、この予測を説明する必要があります。そのアパートの広さは 50m² で、二階にあり、近くに公園があり、猫を飼うことは禁止されています。

公園が近く猫が禁止されている 50m^2^ の二階のアパートの予測価格は €300,000。目的は、これらの特徴量がそれぞれどのように予測値に寄与したのかを説明すること。

FIGURE 5.42: 公園が近く猫が禁止されている 50m² の二階のアパートの予測価格は €300,000。目的は、これらの特徴量がそれぞれどのように予測値に寄与したのかを説明すること。

全アパートの平均予測値は €310,000 です。平均予測値と比較して、それぞれの特徴量の値は予測にどの程度寄与しているでしょうか。

線形回帰モデルの場合、答えは簡単です。各特徴量の効果は、特徴量の重みと値を掛け合わせたものだからです。ただしこれは、モデルが線形なので上手くいっているだけです。より複雑なモデルに対しては、異なる解決策が必要です。例えば、LIME は、効果を見積もるために局所的なモデルを提案します。もう1つの解決策は、協力ゲーム理論に由来します。シャープレイ値は、Shapley (1953)⁴⁰によって提案された方法であり、総報酬額に対する貢献度に応じて参加者に支払額を割り当てる方法です。参加者は、連合とよばれるグループ内で互いに協力し、この協力を通じて一定の利益を受け取ります。

参加者、ゲーム、報酬、これらは、機械学習の予測や解釈可能性に対して、一体何の関係があるのでしょうか。 "ゲーム" とは、データセットの中の1つのインスタンスに対する予測タスクを意味します。 "報酬" は、このインスタンスの実際の予測から全てのインスタンスの予測平均を引いたものです。 "プレイヤー" とは、報酬を受け取るために協力するインスタンスの各特徴量の値です。アパートの例では、park-nearby、cat-banned、area-50 そして floor-2nd という特徴量の値が互いに連携することで €300,000 の予測を達成したということになります。ここで我々の目標は、実際の予測 (€300,000) と平均予測 (€310,000) の違い、つまり -€10,000 の違いを説明することです。

この答えとしては次のようなものが考えられます。 park-nearby は €30,000 の寄与、size-50 は €10,000 の寄与、floor-2nd は €0 の寄与、cat-banned は -€50,000 の寄与。寄与の合計は -€10,000 になり、最終予測から平均予測のアパート価格を差し引いたものになります。

１つの特徴量のシャープレイ値をどのように計算するのでしょうか。

シャープレイ値は、考えうる全ての組み合わせ（連合）にわたる平均周辺寄与 (average marginal contribution) です。これで理解できるしょうか。

次の図では、cat-banned を park-nearby と size-50 の連合に追加するときの寄与を評価します。データから別のアパートをランダム抽出してその値を基準にすることで、park-nearby、cat-banned および size-50 のみが連合をなしている場合をシミュレートします。 floor-2nd がランダム抽出された floor-1st に置き換えられたとします。そしてこの組み合わせでアパート価格を予測した結果は €310,000 です。次のステップでは、cat-banned を連合から取り除いて、それをランダム抽出したアパートから、猫の禁止/許可という値と置き換えます。この例では cat-allowed ですが、cat-banned が再び選ばれるかもしれません。 park-nearby と size-50 の連合のアパート価格を予測すると€320,000です。その結果、cat-banned の寄与は €310,000 - €320,000 = -€10.000 となりました。この見積は、ランダム抽出されたアパート (猫と階の特徴量の値を提供した "ドナー" ) の価格に依存しています。そのため、サンプリングを繰り返して、寄与の平均を計算することで、よりよい推定を行ます。

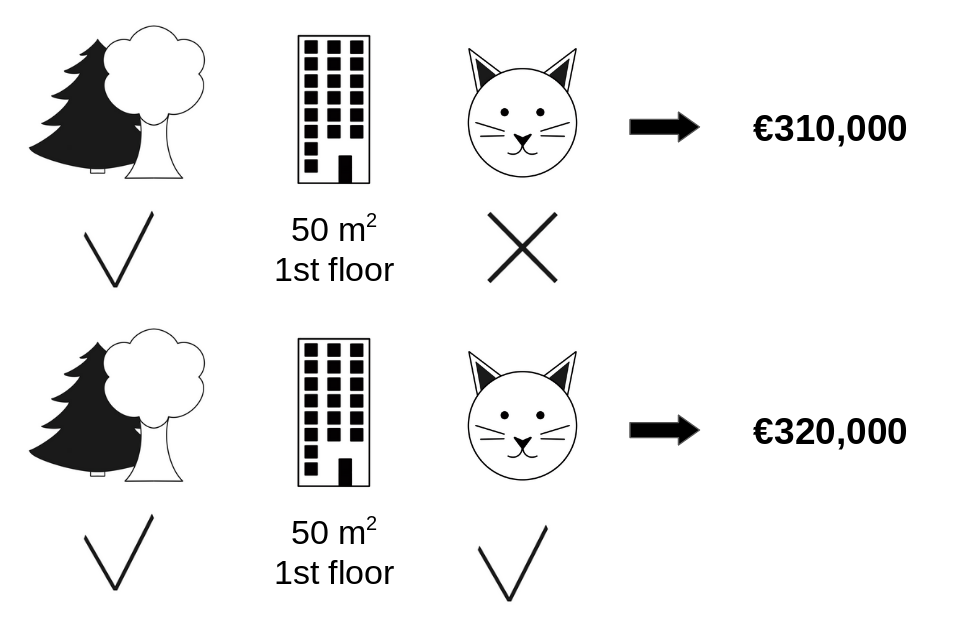
FIGURE 5.43: park-nearby と area-50 の連合に cat-banned を追加する場合の予測に対する寄与を推定するための反復

全ての可能な連合に対して、この計算を繰り返します。シャープレイ値は考えうる全ての連合に対する全ての周辺寄与の平均です。計算時間は、特徴量の数とともに指数関数的に増加します。計算時間を現実的にするための1つの解決策は、連合の少数のサンプルから寄与を計算することです。

次の図は、cat-banned のシャープレイ値を決定するために必要となる特徴量の全ての連合を示しています。最初の行は、特徴量の値がない連合です。 2行目、3行目、4行目は、"|" で区切られた、サイズが増加した様々な連合です。全体としては、以下の連合が可能です。

No feature values
park-nearby
size-50
floor-2nd
park-nearby+size-50
park-nearby+floor-2nd
size-50+floor-2nd
park-nearby+size-50+floor-2nd.

これらの連合のそれぞれについて、cat-banned という特徴量の値がある場合とない場合のアパート価格を予測して、その差を計算することで周辺寄与を求めます。シャープレイ値は、周辺寄与の（加重）平均です。連合に入っていない特徴量の値を、アパートデータセットから取得したランダムな特徴量の値と置き換えて、機械学習モデルで予測値を計算します。

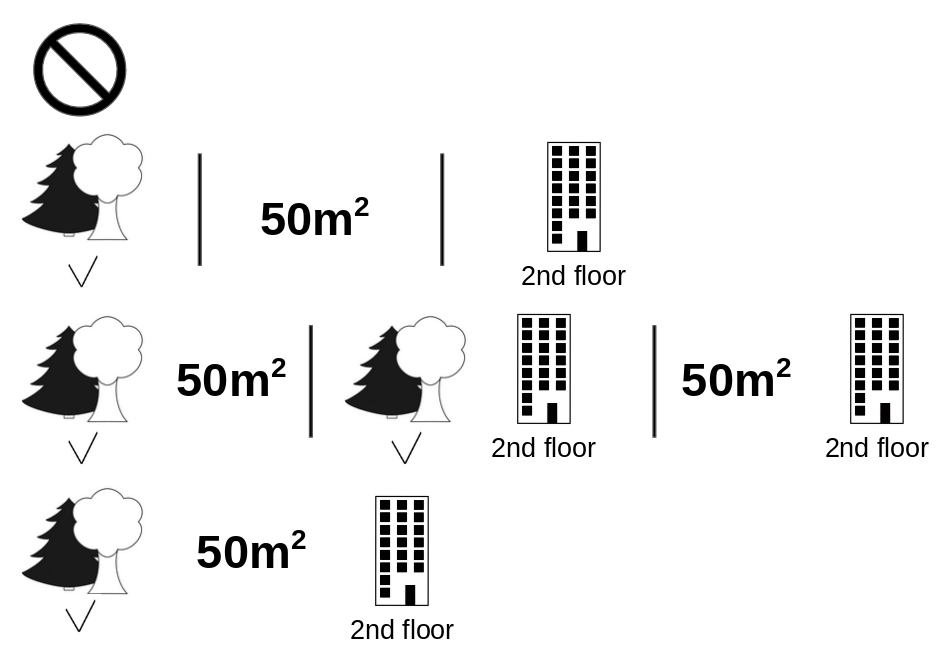
FIGURE 5.44: cat-banned の正確なシャープレイ値を計算するのに必要な8つの連合すべて。

全ての特徴量値に対してシャープレイ値を推定すると、特徴量間の予測の完全な分布（平均を差し引いたもの）が得られます。

5.9.2 例と解釈

特徴量 j のシャープレイ値の解釈は次のようになります。 j 番目の特徴量の値は、データセットの平均予測と比較して、この特定のインスタンスの予測に \(\phi_j\) 寄与しました。

シャープレイ値は分類（確率を扱う場合）と回帰の両方に有効です。

シャープレイ値を使ってランダムフォレストモデルを使用した子宮頸がんの予測を分析します。

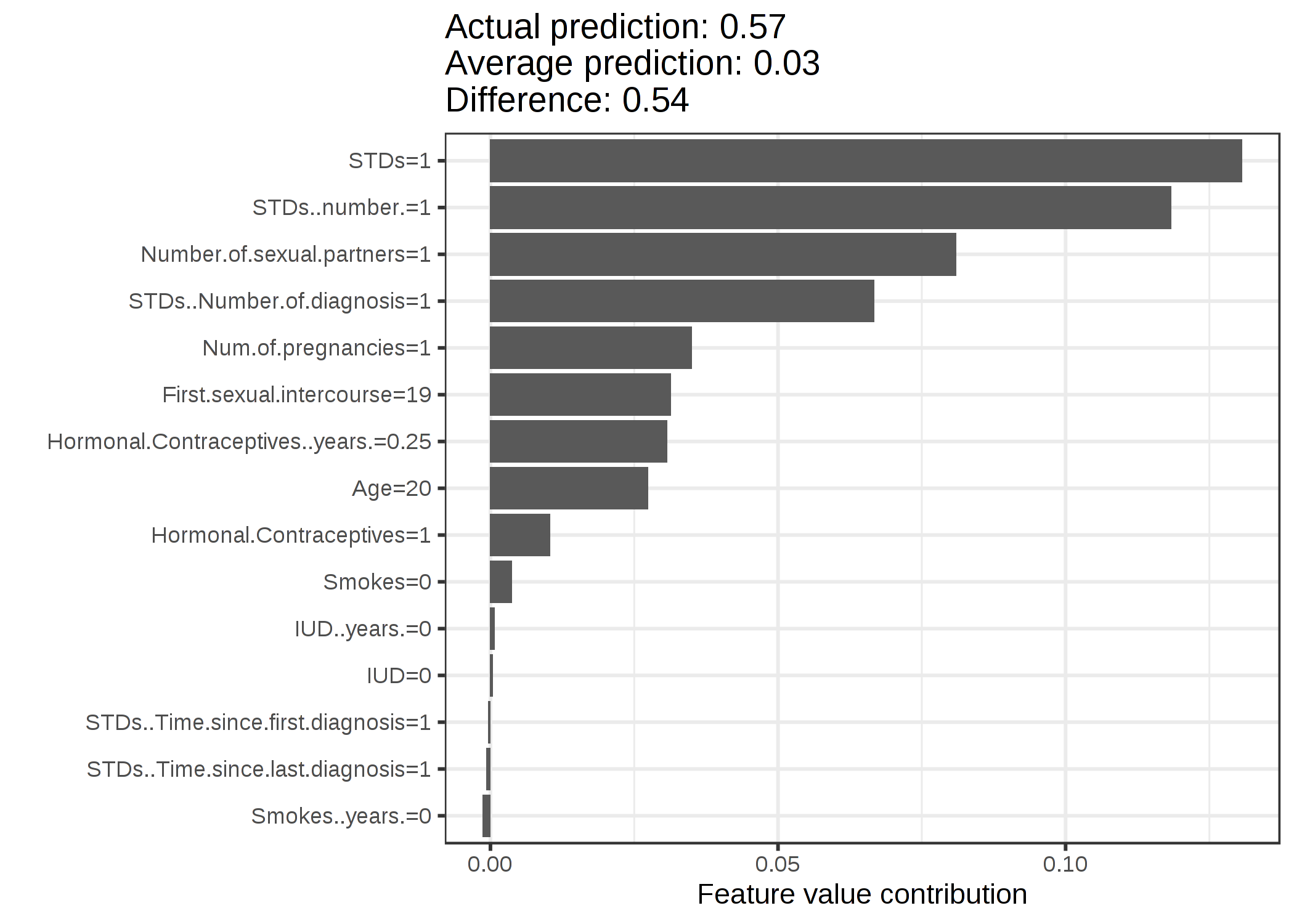
子宮頚がんデータセットのシャープレイ値。0.57の予測では、この女性の癌の確率が平均予測0.03より、0.54だけ高いことを示している。STDsと診断された回数が多いほど確率がもっとも増加する。寄与度の合計は実際の予測と平均予測の差 (0.54) を示す。

FIGURE 5.45: 子宮頚がんデータセットのシャープレイ値。0.57の予測では、この女性の癌の確率が平均予測0.03より、0.54だけ高いことを示している。STDsと診断された回数が多いほど確率がもっとも増加する。寄与度の合計は実際の予測と平均予測の差 (0.54) を示す。

自転車レンタルデータセットに対しても、与えられた天気やカレンダー情報から一日のレンタル数を予測するランダムフォレストを学習させます。そして、特定の日のランダムフォレストの予測を説明します。

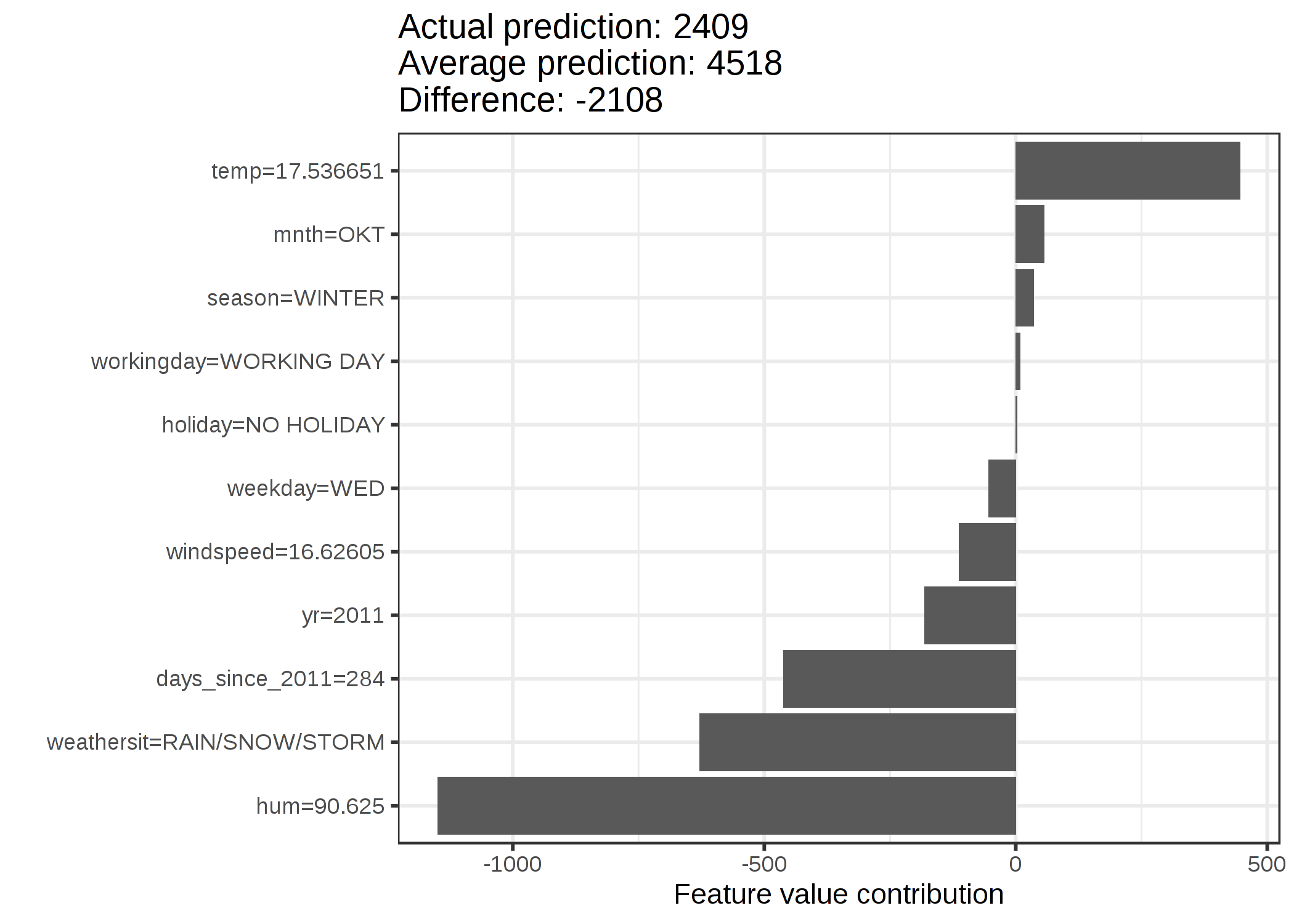
285日目のシャープレイ値。レンタル自転車の予測は 2409 となり、この日は平均予測 4518 より -2108 だけ低い。天候と湿度が最も大きい負の寄与となり、気温は正の寄与があった。シャープレイ値の合計は実際の予測値と予測平均の差 (-2108) になっている。

FIGURE 5.46: 285日目のシャープレイ値。レンタル自転車の予測は 2409 となり、この日は平均予測 4518 より -2108 だけ低い。天候と湿度が最も大きい負の寄与となり、気温は正の寄与があった。シャープレイ値の合計は実際の予測値と予測平均の差 (-2108) になっている。

シャープレイ値を正しく解釈するために、注意すべきことがあります。シャープレイ値は異なる連合の中で、特徴量の値が予測に与える平均寄与であり、モデルから特徴量を削除したときの予測の差ではありません。

5.9.3 シャープレイ値の詳細

この章では好奇心旺盛な読者のためにシャープレイ値の定義と計算について深掘りします。もし、技術的な詳細に興味がなければこの章をスキップして、"長所と短所" に飛んでください。

各特徴量がデータ点の予測にどれだけ影響があるかに興味があります。線形モデルでは各々の効果を計算するのは簡単です。 1つのデータインスタンスに対する線形モデルの予測は次のようになります。

\[\hat{f}(x)=\beta_0+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\]

x を寄与を計算したいインスタンスとします。 \(x_j\) (j = 1, ..., p) はそれぞれ特徴量 j の値とします。 \(\beta_j\) は特徴量 j に対応する重みです。

j 番目特徴量の予測 \(\hat{f}(x)\) に対する寄与 \(\phi_j\) は次のようになります。

\[\phi_j(\hat{f})=\beta_{j}x_j-E(\beta_{j}X_{j})=\beta_{j}x_j-\beta_{j}E(X_{j})\]

ただし、\(E(\beta_jX_{j})\) は特徴量 j の平均効果です。寄与度は特徴量の効果から平均効果を引いた値です。すばらしい！これで各特徴量がどれだけ予測に影響を及ぼしたかが分かります。 1つのインスタンスに対するすべての特徴量の寄与度を合計すると、結果は以下のようになります。

\[\begin{align*}\sum_{j=1}^{p}\phi_j(\hat{f})=&\sum_{j=1}^p(\beta_{j}x_j-E(\beta_{j}X_{j}))\\=&(\beta_0+\sum_{j=1}^p\beta_{j}x_j)-(\beta_0+\sum_{j=1}^{p}E(\beta_{j}X_{j}))\\=&\hat{f}(x)-E(\hat{f}(X))\end{align*}\]

これはデータ点 x の予測値から平均予測値を引いたものです。特徴量の寄与度は負になることもあります。

どんなモデルに対しても同じようにいくでしょうか？モデルに依存しないツールとしてこれがあるといいですね。他のタイプのモデルは同様の重みを持たないことから、異なる解決策が必要です。

助けは意外なところからやってきます。それこそが、協力ゲーム理論に由来するシャープレイ値です。シャープレイ値は任意の機械学習モデルの単一の予測に対する特徴量の寄与度を計算する方法です。

5.9.3.1 シャープレイ値

シャープレイ値は、S の中のプレイヤーの値関数 val を用いて定義されます。

特徴量の値のシャープレイ値は報酬への寄与度であり、特徴量の値の全ての組み合わせに対して、加重和をとったのものです。

\[\phi_j(val)=\sum_{S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j\}}\frac{|S|!\left(p-|S|-1\right)!}{p!}\left(val\left(S\cup\{x_j\}\right)-val(S)\right)\]

ただし、S はモデルで使用されている特徴量の部分集合、x は説明されるインスタンスの特徴量ベクトル、p は特徴量の数を表します。 \(val_x(S)\) は集合 S に含まれていない特徴量で周辺化された集合 S の特徴量の値に対する予測です。

\[val_{x}(S)=\int\hat{f}(x_{1},\ldots,x_{p})d\mathbb{P}_{x\notin{}S}-E_X(\hat{f}(X))\]

実際には、S に含まれていないそれぞれの特徴量に対して多重積分します。具体例として、4つの特徴量 x1、x2、x3、x4 に対する機械学習モデルがあったときに、特徴量 x1 と x3 からなる連合 S の予測値を評価します。

\[val_{x}(S)=val_{x}(\{x_{1},x_{3}\})=\int_{\mathbb{R}}\int_{\mathbb{R}}\hat{f}(x_{1},X_{2},x_{3},X_{4})d\mathbb{P}_{X_2X_4}-E_X(\hat{f}(X))\]

これは線形モデルの特徴量の寄与度に似ています。

"値" という言葉の多用に惑わされないでください。特徴量の値は、インスタンスや特徴の数値(numerical or categorical)です。シャープレイ値は予測に対する特徴量の寄与度です。値関数 (value function) は、プレイヤー（特徴量の値）の連合に対する報酬関数です。

シャープレイ値は効率性、対称性、ダミー、加法性を満たす唯一の方法で、これらを組み合わせることにより、公平な報酬の定義を考えることができます。

効率性: 特徴量の寄与度の合計は x の予測と平均との差である必要があります。

\[\sum\nolimits_{j=1}^p\phi_j=\hat{f}(x)-E_X(\hat{f}(X))\]

対称性: 2つの特徴量の値 j と k の寄与度は、全ての連合に等しく寄与する場合、同じである必要があります。
すなわち、全ての \[S\subseteq\{x_{1},\ldots,x_{p}\}\setminus\{x_j,x_k\}\] について、\[val(S\cup\{x_j\})=val(S\cup\{x_k\})\] ならば、 \[\phi_j=\phi_{k}\] が成立します。

ダミー: 予測値に影響のない特徴量 j は、追加される連合に関係なく、シャープレイ値が 0 になる必要があります。すなわち、すべての \[S\subseteq\{x_{1},\ldots,x_{p}\}\] について \[val(S\cup\{x_j\})=val(S)\] ならば、\[\phi_j=0\] が成立します。

加法性: 結合した報酬 val+val⁺ をもつゲームに対して、それぞれのシャープレイ値は次のようになります。

\[\phi_j+\phi_j^{+}\]

ランダムフォレストを学習したとすると、予測は多くの決定木の平均となります。加法性は各々の決定木のシャープレイ値を計算し、平均を取るとランダムフォレスト全体のシャープレイ値を得られることを保証します。

5.9.3.2 直感

シャープレイ値は次のように直感的に理解できます。特徴量がランダムな順序で部屋に入ります。部屋にいる全ての特徴量はゲームに参加します（= 予測に寄与します）。ある特徴量のシャープレイ値とは、既に部屋にいた特徴量が受ける予測と、その特徴量が加わった時の予測の変化の平均です。

5.9.3.3 シャープレイ値の推定

シャープレイ値を正確に計算するには、特徴量のすべての可能な連合（集合）を \(j\) 番目の特徴量がある場合とない場合とで評価する必要があります。可能な連合の数は特徴量が追加されると指数的に増加するため、この問題の正確な解を得るのは困難になります。 Strumbelj et al. (2014)⁴¹ はモンテカルロサンプリングによる近似を提案しています。

\[\hat{\phi}_{j}=\frac{1}{M}\sum_{m=1}^M\left(\hat{f}(x^{m}_{+j})-\hat{f}(x^{m}_{-j})\right)\]

ここで、\(\hat{f}(x^{m}_{+j})\) は x に対する予測ですが、\(j\) 番目の特徴量の各値を除いて、ランダムな数の特徴量がランダムなデータ点 \(z\) からの特徴量に置き換えられています。ベクトル \(x^{m}_{-j}\) はほとんど \(x^{m}_{+j}\) と同じですが、\(x_j^{m}\) もサンプリングされた \(z\) から得られます。これらの \(M\) 個の新しいインスタンスはそれぞれ、2つのインスタンスから組み立てられた一種の「フランケンシュタインの怪物」です。

1つの特徴量値に対するシャープレイ値の概算

出力: j 番目の特徴量の値に対するシャープレイ値
入力: 反復回数 M、関心のあるインスタンス x、特徴量のインデックス j、データ行列 X、および機械学習モデル f
すべての m = 1,...,M について
- データ行列 X からランダムなインスタンス z を抽出する
- 特徴量のランダムな並べ替え o を選択する
- o に従ってインスタンス x を並べる: \(x_o=(x_{(1)},\ldots,x_{(j)},\ldots,x_{(p)})\)
- o に従ってインスタンス z を並べる: \(z_o=(z_{(1)},\ldots,z_{(j)},\ldots,z_{(p)})\)
- 2つの新しいインスタンスを構築する
  - j 番目の特徴量がある場合: \(x_{+j}=(x_{(1)},\ldots,x_{(j-1)},x_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
  - j 番目の特徴量がない場合: \(x_{-j}=(x_{(1)},\ldots,x_{(j-1)},z_{(j)},z_{(j+1)},\ldots,z_{(p)})\)
- 周辺寄与を算出する: \(\phi_j^{m}=\hat{f}(x_{+j})-\hat{f}(x_{-j})\)
平均値としてシャープレイ値を計算する: \(\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\)

まず、関心のあるインスタンス x、特徴量 j、反復回数 M を選択します。繰り返しごとに、データからランダムなインスタンス z を選択し、特徴量のランダムな順序を生成します。関心のあるインスタンス x とサンプル z の値を組み合わせて、2つの新しいインスタンスが生成されます。インスタンス \(x_{+j}\) が関心のあるインスタンスですが、特徴量 j より前の順序の値はすべてサンプル z からの特徴量で置き換えられます。インスタンス \(x_{-j}\) は \(x_{+j}\) と同じですが、さらに特徴量 j の値がサンプル z からの特徴量 j の値で置き換えられています。そして次のようにブラックボックスからの予測値の差が計算されます。

\[\phi_j^{m}=\hat{f}(x^m_{+j})-\hat{f}(x^m_{-j})\]

これらの差をすべて平均すると、シャープレイ値が得られます。

\[\phi_j(x)=\frac{1}{M}\sum_{m=1}^M\phi_j^{m}\]

平均することによって、暗黙のうちにXの確率分布によってサンプルに重みづけされます。

すべての特徴量についてのシャープレイ値を得るため、この手順を各特徴量に対して繰り返す必要があります。

5.9.4 長所

予測と予測の平均の差分は、シャープレイ値の効率性という性質から、インスタンスの特徴量間で公平に分配されます。この性質により、シャープレイ値は LIME などの他の手法と区別されます。 LIME は予測が特徴量間で公平に分配されることを保証しません。 EU の「説明を求める権利」のように、法が説明を求める状況下において、シャープレイ値は確かな理論に基づき、予測を公平に分配しているため、法に準拠した唯一の手法であるかもしれません。ただし、筆者は法律家ではないので、これは法の要請に対する著者の直感でしかありません。

シャープレイ値は対照的な説明を可能にします。予測をデータセット全体の予測の平均と比較する代わりに、データの部分集合や単一のデータとも比較できます。この性質もまた、LIME のような局所モデルにはないものです。

シャープレイ値は確かな理論に基づいた唯一の説明手法です。効率性、対称性、ダミー、加法性の原理により説明に合理的な根拠が与えられます。 LIME のような手法は機械学習モデルが局所的には線形に振る舞うことを仮定しますが、これがうまくいく理由についての理論はないのです。

特徴量によってプレイされるゲームとして予測を説明するというのは驚くべきことです。

5.9.5 短所

シャープレイ値は、多くの計算時間 を必要とします。実世界の問題の99.9%では、近似解しか求めることができません。シャープレイ値の厳密な計算は、特徴量の 2^k の可能な連合があり、特徴量の "不在" はランダムなインスタンスを描くことでシミュレートしなければならず、シャープレイ値の推定値の分散が大きくなるため、計算量が多くなります。連合の指数関数的な数は、連合をサンプリングし、反復回数 M を制限することで対処します。 M を減らすと計算時間は短縮されますが、シャープレイ値の分散が大きくなります。反復回数 M には良い経験則はありません。 Mは、シャープレイ値を正確に推定するのに十分な大きさでなければなりませんが、妥当な時間で計算を完了するのに十分な小ささである必要もあります。チェルノフ・バウンズに基づいて M を選択できますが、機械学習予測のためのシャープレイ値についてこれを行った論文を見たことはありません。

シャープレイ値は誤解される可能性があります。特徴量のシャープレイ値は、モデル学習から特徴量を除去した後の予測値の差ではありません。シャープレイ値は、「現在の特徴量の値の集合が与えられたときの、実際の予測値と平均予測値の差に対する特徴量の寄与度」であると解釈してください。

スパースな説明（特徴量をほとんど含まない説明）を求める場合、シャープレイ値は不適切な説明方法です。シャープレイ値は常にすべての特徴を使う説明を作成します。人はLIMEのような選択的な説明を好みます。一般の人が扱わなければならない説明には、LIMEの方が適しているかもしれません。もう1つの解決策として、Lundberg and Lee (2016)⁴²が紹介しているSHAPがあります。これはシャープレイ値をベースにしていますが、特徴量の少ない説明も可能です。

シャープレイ値は特徴量あたりの単純な値を返しますが、LIMEのような予測モデルはありません。つまり、「年収が300ユーロ増えると、私のクレジットスコアは5ポイント上昇します。」というような入力の変化に対する予測の変化についての記述には使えません。

もう1つの欠点は、新しいインスタンスのシャープレイ値を計算したい場合、データへのアクセスが必要になることです。対象のインスタンスの一部をランダムに選ばれたインスタンスからの値に置き換えるデータが必要なため、予測関数にアクセスできるだけでは十分ではありません。これは、実際のインスタンスのように見えるがそうではないデータを、学習データから作成できる場合にのみ回避できます。

他の多くの並べ替えに基づく解釈法と同様に、シャープレイ値による手法も、特徴量に相関がある場合、非現実的なデータインスタンスが含まれているという問題があります。連合から特徴値が欠落していることをシミュレートするために、特徴量を周辺化します。これは、特徴量の周辺分布から値をサンプリングすることで達成されます。特徴量が独立であれば問題ありませんが、特徴量が依存関係にある場合、このインスタンスに対して意味をなさない特徴量の値をサンプリングするかもしれません。しかし、特徴量のシャープレイ値を計算するためにそれらの値を利用します。これは、相関のある特徴量を一緒に変化させて、それらの特徴量のために1つの相互シャープレイ値を得ることで解決できるかもしれません。もう1つの解決策は，条件付きサンプリングです。特徴量は、すでに連合にある特徴量に条件をつけてサンプリングされます。条件付きサンプリングにより、非現実的なデータ点の問題は修正できますが、新たな問題があります。 Sundararajan et.al. (2019)⁴³によって発見され、さらにJanzing et.al. (2020)⁴⁴によって議論されているように、結果として得られる値は対称性の公理に反しているので、我々のゲームにとってのシャープレイ値ではありません。

5.9.6 ソフトウェアと代替手法

R では、シャープレイ値は iml と fastshap のパッケージで実装されています。

シャープレイ値の代替推定手法である SHAP は次の章で紹介されています。

他には、breakDown と呼ばれる手法があり、Rのパッケージ breakDown⁴⁵ で実装されています。 breakDown もまた、各特徴量の予測への寄与を示しますが、breakDown ではそれを段階的に計算します。ゲームの例えを再び用いましょう。空のチームからスタートし、予測に最も寄与している特徴量を追加し、これを全ての特徴量が追加されるまで繰り返します。各特徴量がどのくらい予測に貢献するのかは、すでに「チーム」に属しているそれぞれの特徴量に依存しています。これが breakDown メソッドの大きな欠点です。 breakDown はシャープレイ値法よりも高速であり、相互作用のないモデルの場合には同じ結果を与えます。

Shapley, Lloyd S. "A value for n-person games." Contributions to the Theory of Games 2.28 (1953): 307-317.↩
Štrumbelj, Erik, and Igor Kononenko. "Explaining prediction models and individual predictions with feature contributions." Knowledge and information systems 41.3 (2014): 647-665.↩
Lundberg, Scott M., and Su-In Lee. "A unified approach to interpreting model predictions." Advances in Neural Information Processing Systems. 2017.↩
Sundararajan, Mukund, and Amir Najmi. "The many Shapley values for model explanation." arXiv preprint arXiv:1908.08474 (2019).↩
Janzing, Dominik, Lenon Minorics, and Patrick Blöbaum. "Feature relevance quantification in explainable AI: A causal problem." International Conference on Artificial Intelligence and Statistics. PMLR, 2020.↩
Staniak, Mateusz, and Przemyslaw Biecek. "Explanations of model predictions with live and breakDown packages." arXiv preprint arXiv:1804.01955 (2018).↩