4.1 線形回帰
線形回帰モデルは予測値を特徴量の重み付き和として表します。 学習された関係の線形性が解釈を簡単にしてくれます。 線形回帰モデルは長い間、定量的な問題に取り組む統計学者や計算機科学者たちによって使用されてきました。
線形モデルでは、特徴量 x が目的変数 y にどれくらい依存するかをモデリングできます。 学習された関係は線形で、1つのデータ i に対して次のように表すことができます。
\[y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon\]
予測結果は p 個の特徴量の重み付き和です。 \(\beta_{j}\) は学習された特徴の重み、つまり係数を表します。 1つ目の重み (\(\beta_0\)) は切片と呼ばれ、特徴量と乗算はしません。 \(\epsilon\) は予測と実際の結果との差、つまり誤差です。 これらの誤差値はガウス分布に従うと仮定されます。誤差が正の方向にも負の方向にも存在して、小さい誤差は多く、大きい誤差は少ないと仮定するという意味です。
最適な重みを推定するために様々な方法が用いられます。 実際の結果と推定結果との差の二乗和を最小化するような重みを求めるために、最小二乗法がよく用いられます。
\[\hat{\boldsymbol{\beta}}=\arg\!\min_{\beta_0,\ldots,\beta_p}\sum_{i=1}^n\left(y^{(i)}-\left(\beta_0+\sum_{j=1}^p\beta_jx^{(i)}_{j}\right)\right)^{2}\]
具体的に最適な重みがどう求められるかはここでは論じませんが、興味があれば、"The Elements of Statistical Learning" (Friedman, Hastie and Tibshirani 2009)16 の 3.2 章や他の線形回帰に関するオンライン資料を参考にしてください。
線形回帰の最大の利点は線形性です。 線形性により予測手順が簡単になります。最も重要なことは、これらの一次方程式がモジュールレベル(つまり重み)で理解しやすくなります。 これが、線形モデルおよび同様のモデルが、医学、社会学、心理学の学術分野および他の多くの定量的研究分野で広く普及している主な理由の 1つです。 例えば、医療分野では、患者の臨床成果の予測だけでなく、薬の影響を定量化し、同時に性別、年齢、その他の特徴を解釈可能な方法で考慮することが重要です。
推定される重みには信頼区間があります。 信頼区間とは、ある信頼度で「真」の重みを含むような重み推定の範囲です。 例えば、重み2に対する信頼度 95% の信頼区間は1から3の範囲になる可能性があります。 この信頼区間は、「回帰モデルが与えられるデータに正しいという仮定のもとで、新しくサンプリングされたデータに対して推定を 100 回繰り返したときに、この信頼区間は 100 回中 95 回真の重みを含む」と解釈できます。
モデルが「正しい」かはデータ中の関係が、線形性、正規性、等分散性、独立性、固定された特徴量、また、多重共線性の欠如 というこれらの仮定を満たしているかどうかによります。
線形性 線形回帰モデルは予測が特徴量の線形結合になることを要請しますが、これは線形回帰の最大の強みでもあり、最大の制約でもあります。 線形性は解釈可能なモデルに繋がります。 線形効果は定量化しやすく、説明しやすいです。 線形的に足されるため、効果を分離することも簡単です。 特徴量の相互作用や、特徴量と目的値の間の非線形性が疑われる場合は、相互作用項を追加するか、スプライン回帰を使うことができます。
正規性 与えられた特徴量に対する目的値は正規分布に従うと仮定されます。 もしこの仮定が破れると、特徴量に対する重みの推定信頼区間は意味を持たなくなります。
等分散性 誤差項の分散は、特徴空間全体において一定であると想定されます。 平方メートルで与えられる居住面積に基づいて住宅の価格を予測するとします。 家の大きさに関わらず、予測値における誤差の分散が一定であると想定する線形モデルを作ります。 この仮定は、実際には現実に反します。 住宅の例でいうと、家の価値が高いほど価格変動の余地が大きく、価格の予測値における誤差項の分散が大きくなるかもしれません。 線形回帰モデルの平均誤差(予測価格と実際の価格との差)が 50,000 ユーロであるとしましょう。 等分散性を想定すると、平均 50,000 の誤差が 100 万ユーロの家と 4 万ユーロの家とに対して同じであるとすることになります。 これは家の価格がマイナスになりうるということになり、合理的ではありません。
独立性 各データは互いに独立であることが想定されます。 患者ごとに血液検査を複数回行うなど、繰り返して測定する場合、データ点は互いに独立になりません。 従属なデータに対しては混合効果モデルや GEE などの特殊な線形回帰モデルが必要です。 このような場合に、「標準的な」線形回帰モデルを使ってしまうと、モデルから誤った結論を導き出してしまう恐れがあります。
固定された特徴量 入力特徴量は「固定されている」と見なします。 固定されているとは、入力特徴量が統計的な変数でなく、「与えられた定数」として扱われるということです。 これは測定誤差がないことを意味します。 これは、かなり非現実的な仮定です。 しかし、この仮定なしでは、入力特徴の測定誤差を説明するために非常に複雑な測定誤差モデルを使う必要があります。 通常、そんなことはしたくないでしょう。
多重共線性の欠如 強い相関関係にある特徴量は、重みの推定を台無しにするので望ましくありません。 2つの特徴量が強く相関している場合、特徴量の効果が相加的であり、相関する特徴量のどちらが影響を与えているのか不定となるため、重みを推定するときに確定できません。
4.1.1 解釈
線形回帰モデルの重みの解釈は、対応する特徴量のタイプに依存します。
- 量的特徴量 (Numerical feature): 量的特徴量の値が1単位分増えると、推定結果が重み分変化します。量的特徴量の一例としては、家の大きさが挙げられます。
- バイナリ特徴量 (Binary feature): それぞれのインスタンスごとに、2つの値のどちらか一方のみを取る特徴量のことです。 そのような特徴量の一例として、庭付きの家であるかどうかが挙げられます。値のうちの1つは"庭付きでない"のような参照カテゴリ(プログラミング言語によっては 0 と符号化されます)として数えられます。ある特徴量の参照カテゴリが別のカテゴリに変化すると、推定結果は特徴量の重み分変化します。
- 複数のカテゴリを含んだカテゴリカル特徴量: 取りうる値の数が固定された特徴量のことです。一例として、"カーペット"、"ラミネート"、"寄木細工"というカテゴリを取りうる”床の種類”という特徴量が挙げられます。 多くのカテゴリを扱う解決策の1つとして、one-hot エンコーディングというものがあります。one-hot エンコーディングとは、それぞれのカテゴリごとに 0, 1 の値を取るカラムを設定するエンコーディングの手法です。 L 個のカテゴリがあるカテゴリカル特徴量に対しては、L-1 個のカラムがあれば十分です。なぜならば、L 番目のカラムは冗長な情報だからです(例えば、ある1つのインスタンスに対して 1 番目から L-1 番目のカラムが全て 0 であるとき、そのインスタンスのカテゴリは L 番目のものであることが分かるからです)。 各カテゴリに対する解釈はバイナリ特徴量に対する解釈と同じです。 R のような言語では、この章で後ほど説明するような様々な方法でカテゴリカル特徴量をエンコードすることが出来ます。
- 切片\(\beta_0\): 切片は、全てのインスタンスについて常に1をとる”定数特徴量”に対する重みであるとみなすことが出来ます。 大抵のソフトウェアパッケージは切片を推定するために定数特徴量を自動的に追加します。 これに対する解釈は以下の通りです。 全ての量的特徴量が0であり、カテゴリカルデータの値が参照カテゴリであるインスタンスの場合には、モデルの予測値は切片の重みになります。 そのような、全ての特徴量の値が0であるようなインスタンスは多くの場合意味をなさないため、切片の解釈は通常関係がありません。 切片の解釈は、全ての特徴量が平均0、標準偏差1に標準化されているときにのみ意味があるものとなります。 そのような場合、切片は全ての特徴量が平均値であるようなインスタンスの予測結果を反映しています。
線形回帰モデルの特徴量の解釈は以下のテンプレートを用いて自動化できます。
量的特徴量の解釈
特徴量 \(x_{k}\) が 1 だけ増えて、その他の特徴量は固定されている場合、予測結果 y は \(\beta_k\) だけ増えます。
カテゴリカル特徴量の解釈
特徴量 \(x_{k}\) が参照カテゴリから他のカテゴリに変化し、その他の特徴量は固定されている場合、予測結果 y は \(\beta_{k}\) だけ増えます。
もう1つの重要な指標は、決定係数 \(R^2\) です。 \(R^2\) はモデルによって、どの程度、目的値の全てのばらつきが説明されているかを教えてくれます。 \(R^2\) が高くなればなるほど、そのモデルはデータを説明していることになります。 \(R^2\) の計算方法は以下の通りです。
\[R^2=1-SSE/SST\]
SSE は、二乗和誤差 (Squared Sum of the Error)です。
\[SSE=\sum_{i=1}^n(y^{(i)}-\hat{y}^{(i)})^2\]
SST は、データの分散の二乗和です。
\[SST=\sum_{i=1}^n(y^{(i)}-\bar{y})^2\]
SSE は線形回帰で学習した後、どの程度のばらつきが残っているかを教えてくれます。これは、予測と実際の目的値の間の二乗誤差を計測することで求めます。 SST はデータ自体の目的値の全体の分散です。 \(R^2\) は、線形モデルによって、どの程度ばらつきが説明できているのかを教えてくれます。 \(R^2\) は 0 のとき、モデルはデータを全く説明できていないのに対して、1 のときは、データのばらつきを完全に説明できていることを意味します。
実は、たとえ目的値に対する情報を全く含んでいない特徴量を付け加えたとしても、モデルの特徴量の数を増やすと \(R^2\) の値を増加させることができます。 そのため、モデルで使われている特徴量の数を反映した、自由度調整済みの決定係数 \(R^2\) を使用することが推奨されます。 その計算方法は次のようになります。
\[\bar{R}^2=1-(1-R^2)\frac{n-1}{n-p-1}\]
ただし、 p は特徴量の数で、n はインスタンスの数です。
(自由度調整済み)決定係数 \(R^2\) がとても低いモデルに対しては、そもそもモデルがデータをうまく説明できていないため、そのモデルの解釈をしても意味がありません。 どのように重みの解釈しても、意味がないでしょう。
特徴量重要度 (Feature Importance)
線形回帰モデルの特徴量の重要度は t 統計量の絶対値で計測できます。 t 統計量は標準誤差でスケーリングされた推定重みです。
\[t_{\hat{\beta}_j}=\frac{\hat{\beta}_j}{SE(\hat{\beta}_j)}\]
この式は何を意味しているのでしょうか。 特徴量の重要度は、重みが増えると増加します。 これは理にかなっています。 推定された重みに、よりばらつきがあると (正しい値に関しての確証が小さくなる)、その特徴量に対する重要度は小さくなります。 これも理にかなっています。
4.1.2 例
この例では、線形回帰モデルを使って、天気や日付情報が与えられたときの自転車レンタル台数 の予測をします。
解釈のために、回帰の重みについて調べます。 特徴量は、量的特徴量、カテゴリカル特徴量のどちらもがあります。 各特徴に対して、推定された重み、推定値の標準誤差 (SE)、及び t 統計量の絶対値(|t|)を表に示します。
| Weight | SE | |t| | |
|---|---|---|---|
| (Intercept) | 2399.4 | 238.3 | 10.1 |
| seasonSUMMER | 899.3 | 122.3 | 7.4 |
| seasonFALL | 138.2 | 161.7 | 0.9 |
| seasonWINTER | 425.6 | 110.8 | 3.8 |
| holidayHOLIDAY | -686.1 | 203.3 | 3.4 |
| workingdayWORKING DAY | 124.9 | 73.3 | 1.7 |
| weathersitMISTY | -379.4 | 87.6 | 4.3 |
| weathersitRAIN/SNOW/STORM | -1901.5 | 223.6 | 8.5 |
| temp | 110.7 | 7.0 | 15.7 |
| hum | -17.4 | 3.2 | 5.5 |
| windspeed | -42.5 | 6.9 | 6.2 |
| days_since_2011 | 4.9 | 0.2 | 28.5 |
量的特徴量の解釈について (temperature): 摂氏が1度上昇したとき、他の特徴量は全て同じとすると、自転車のレンタル台数の予測は 110.7 だけ増加します。
カテゴリカル特徴量の解釈について (weathersit): 自転車のレンタル数の予測値は、天気の良い日と比べて、雨や雪や嵐のとき -1901.5 だけ変化します。ただし、このときも他の特徴量は変化しないことを想定しています。 晴れた日に比べて、霧が濃い時は、自転車のレンタル台数の予測値は -379.4 だけ変化します。
全ての解釈では必ず、"他の特徴量は変化させない"という脚注がついています。 これは、線形回帰モデルの性質です。 予測値は、重み付けされた特徴量の線形和です。 推定された線形方程式は特徴量/予測値空間の超平面です (単一の特徴量の場合単純な直線になります)。 重みは各方向の超平面の傾き(勾配)を指定しています。 良い点としては、加法性によって個々の特徴量の効果を他の全ての特徴量から分離できることです。 これが可能なのは、全ての特徴量の効果(重みと特徴量の積)が和によって組み合わされているからなのです。 悪い点としては、この解釈は特徴量の同時分布を無視していることです。 ある特徴量を増やすが、他の特徴量は変化させないとき、非現実的か好ましくないデータが得られるかもしれません。 例えば、家の大きさを広くすることなく、部屋の数を増加させることは現実的ではないでしょう。
4.1.3 可視化による解釈
種々の可視化手法を用いることで、線形回帰モデルを簡単かつ素早く把握できます。
4.1.3.1 重みプロット (Weight Plot)
重みの情報(重みと分散の推定値)は重みプロットを用いることで簡単に可視化できます。 以下のプロットでは、先ほどの線形回帰の結果を可視化しています。
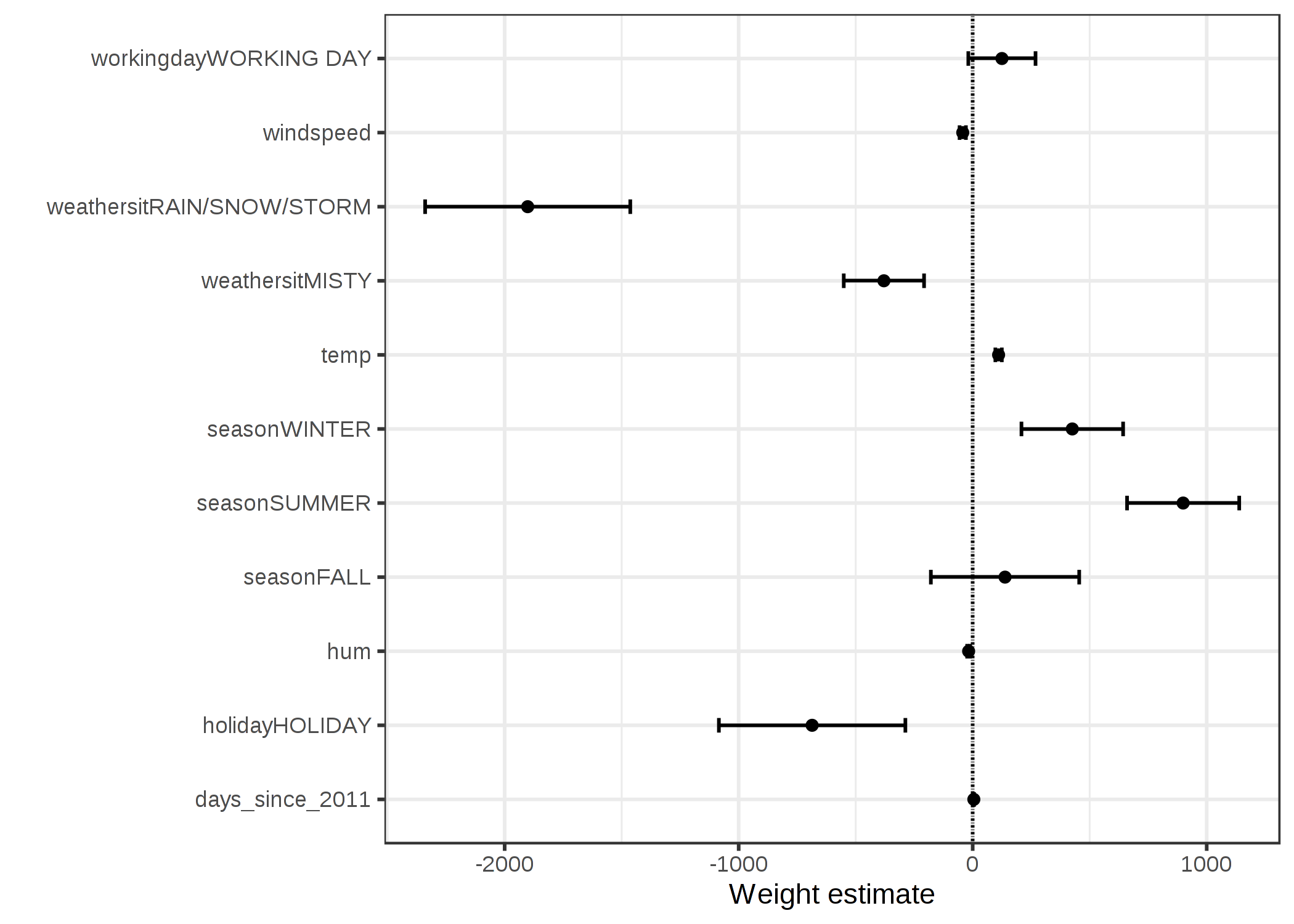
FIGURE 4.1: 重みが点として、95%信頼区間が線として表示されている。
重みプロットは、自転車のレンタル台数を予測するにあたって、雨、雪、嵐といった天気は大きな負の影響を及ぼすことを示しています。 仕事日の重みはほぼ 0 になっており、かつ 95% 信頼区間に 0 は含まれています。従って、この特徴量は統計的に重要でないことが示されます。 信頼区間が非常に短く推定値は 0 に近くとも、対応する特徴量の効果が統計的に有意な場合がありました。 気温についても同様のことが言える可能性があります。 重みプロットにおける問題は、各特徴量が異なるスケールで計測されているということです。 天気の推定された重みは晴れ、雨、嵐、雪のそれぞれの天気の違いを反映していますが、気温は 1 度の変化による影響を反映しています。 特徴をスケーリングすることで、線形回帰モデルを学習させる前に、推定された重みを比較できるようになります。(例えば標準化など)
4.1.3.2 影響力プロット (Effect Plot)
線形回帰モデルの重みは特徴量と掛け合わせることで、より意味のある分析になり得ます。重みは特徴量のスケールに依存し、例えば身長の単位をメートルからセンチメートルに変更すればまた異なる重みになります。 ただ、重みは変化したとしても、重みが実際にデータに及ぼす影響は変化しません。 また特徴量の分布を知ることは重要です。なぜなら、ある特徴量の分散が非常に低い場合、ほとんどのインスタンスがその特徴量から同じような影響を受けることを意味するからです。 影響力プロットは、重みと特徴の組み合わせがどれほど予測に貢献しているかを理解する助けになります。 影響力を計算するのは、各特徴ごとの重みと、特徴量をインスタンスごとに掛け合わせます。
\[\text{effect}_{j}^{(i)}=w_{j}x_{j}^{(i)}\]
影響力は箱ひげ図を用いて可視化できます。 箱ひげ図内の各箱は、全データのうち半分のデータに対する影響力の範囲を表します(第1四分位点から第3四分位点まで)。箱内の縦線は中央値を表します。つまり、予測時に半数のインスタンスはこれよりも低い影響力をもち、もう半数は高い影響力を持つということです。 横線は \(\pm1.5\text{IQR}/\sqrt{n}\) まで引かれていて、IQR は四分位範囲(inter quartile range)(第3四分位数から第1四分数を引いたもの)のことです。
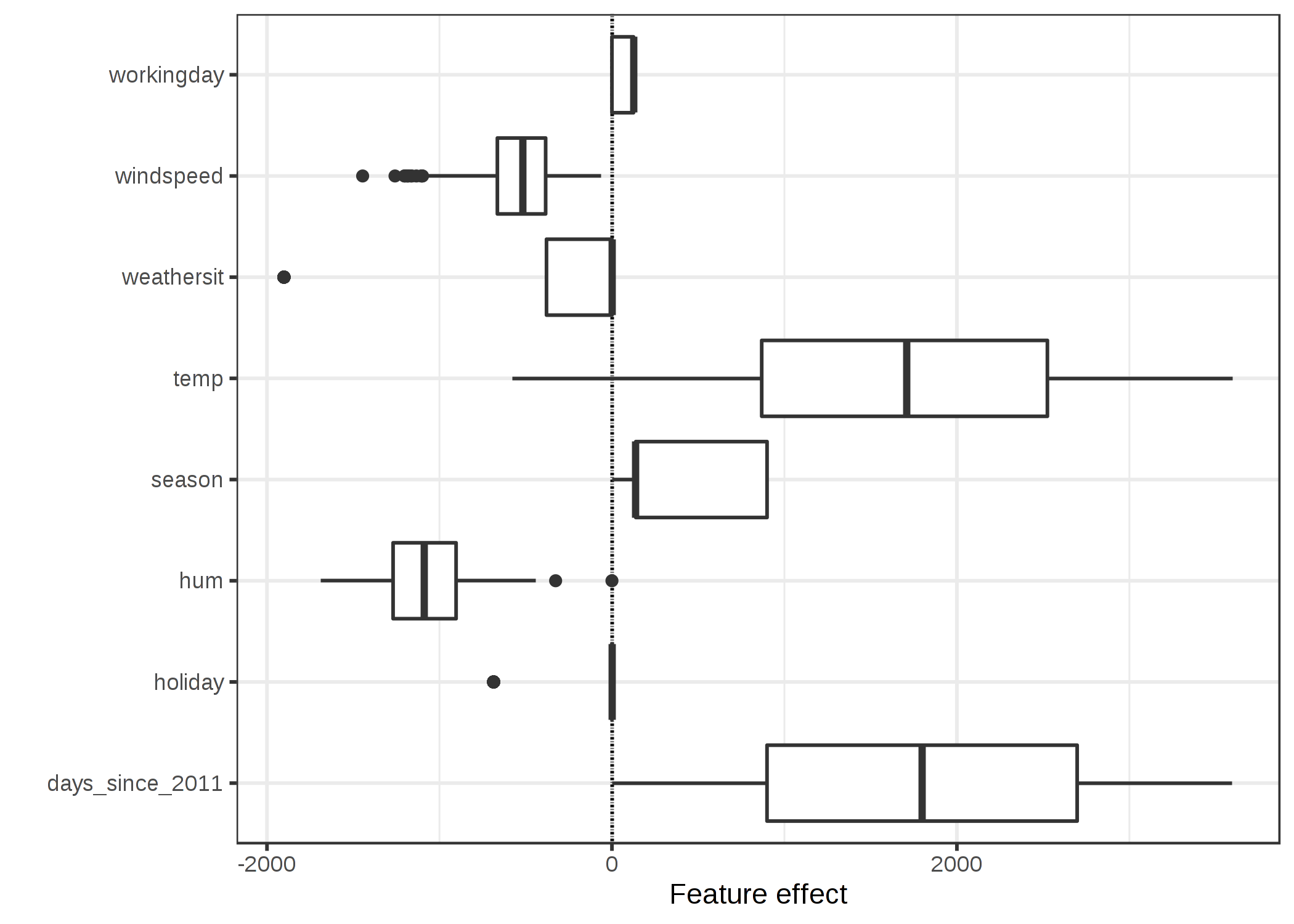
FIGURE 4.2: 特徴量の影響力プロットは、特徴量ごとのデータに対する影響 (特徴量と重みの積) の分布を示している。
図から、自転車のレンタル台数の予測に大きく寄与している特徴量は、気温と日数の特徴であることがわかります。この特徴量は、自転車レンタルのトレンドを捉えていると言えます。 気温が予測にどれだけ寄与しているかの範囲はかなり広くなっています。日数の特徴量は 0 から大きな正の値に渡って寄与していることがわかります。これは、データセット内での初日(2011/1/1)ではトレンドの影響は非常に小さく、かつ推測された重みは正の値 (4.93) だったからです。これが意味するのは、影響力は毎日上昇し続け、データセット内の最終日(2013/12/31)に最大値を迎えるということです。 重みが負の値のとき、あるインスタンスが正の影響力を持っていたとすると、特徴量が負であるということに注意してください。 例えば、風速が大きく負の影響力を持っているような日は、風速がかなり強い日であるということです。
4.1.4 個々の予測に対する説明
あるインスタンスの各特徴量はどれだけ予測に貢献したのでしょうか。 この疑問への回答はインスタンスに対する効果を計算することで得られます。 インスタンスに固有の効果の解釈は各特徴量に関する効果の分布を比較することでのみ意味を持ちます。 自転車データセットの6番目のインスタンスに対する線形モデルの予測について説明します。 このインスタンスは以下の特徴量をもっています。
| Feature | Value |
|---|---|
| season | SPRING |
| yr | 2011 |
| mnth | JAN |
| holiday | NO HOLIDAY |
| weekday | THU |
| workingday | WORKING DAY |
| weathersit | GOOD |
| temp | 1.604356 |
| hum | 51.8261 |
| windspeed | 6.000868 |
| cnt | 1606 |
| days_since_2011 | 5 |
このインスタンスの特徴量の効果を知るため、その特徴量と、それに対応する線形回帰モデルの重みの積を求めなくてはなりません。 特徴量 "workingday" の値 "WORKING DAY" に対する効果は 124.9 となります。 気温 1.6 度の効果は 177.6 です。 これらの個々の効果をデータ全体への効果の分布を示す図にX印としてプロットします。 これにより個々の効果とデータ全体の効果が比較できます。
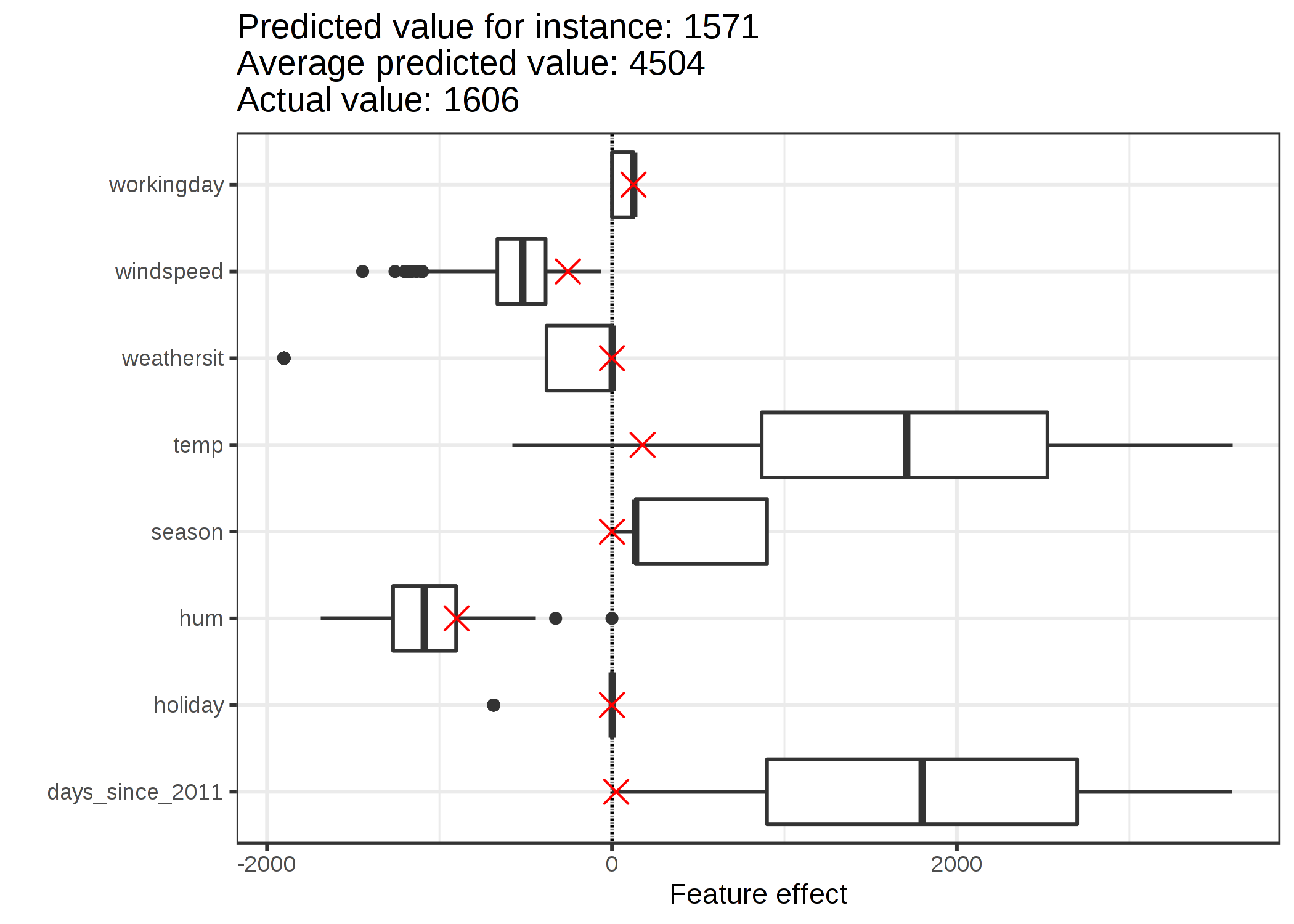
FIGURE 4.3: 1つのインスタンスに対する影響力プロットは、影響力の分布を示し、興味のあるインスタンスの効果のハイライトする。
訓練データのインスタンスに対する予測を平均すると、4504 の平均となります. それと比較すると、6 番目のインスタンスによる自転車の台数予測は 1571 しかないことから、小さいといえます。 影響力プロットはその理由を明らかにしています。 箱ひげ図はデータセットにおける全インスタンスの効果分布を表し、X印は 6 番目のインスタンスの効果を示しています。 6 番目のインスタンスは、この日の気温が 2 度であり、その他のほとんどの日と比べて気温が低いことから、気温による寄与が小さいと言えます ( 気温に対する重みは正であることに注意)。 また、トレンド特徴量である "days_since_2011" の効果も、このインスタンスが2011初頭(5 days) のものであることと、トレンドに対する重みが正であることから、寄与が小さいと言えます。
4.1.5 カテゴリカル特徴量のエンコーディング
カテゴリカル特徴量をエンコーディングする方法は複数あり、選択した方法によって重みの解釈に影響が生じます。
線形回帰モデルにおいて標準となるのは treatment coding で、これは多くの場合で十分に機能します。 異なるエンコーディングの手法は1つのカテゴリカル特徴量から異なる計画行列を作り出すことに相当します。
この節では3つの異なるエンコーディングの方法について紹介しますが、他にも多くの手法が知られています。 使用する例では、6つのインスタンスと3つのカテゴリを持つカテゴリカル特徴量を持ちます。 最初の2つのインスタンスでは、特徴量はカテゴリAを取ります。 3番目、4番目のインスタンスでは、カテゴリーBを取り、最後2つのインスタンスはカテゴリーCを取ります。
Treatment coding
treatment coding では、カテゴリごとの重みは、対応するカテゴリと参照カテゴリ間の予測の差の推定値とします。 線形モデルの切片は参照カテゴリの平均値です。(他の全ての特徴量が変わらない場合)
計画行列の最初の列は切片で常に 1 となります。 2 列目はインスタンス i がカテゴリ B かどうかを示しており、3 列目はインスタンスがカテゴリ C かどうかを示しています。
線形方程式が過剰になり、重みに対して一意な解を見つけることができなくなるため、カテゴリ A に対する列は必要ありません。 インスタンスがカテゴリ B にも C にも属していないことがわかれば十分なのです。
Feature matrix:
\[\begin{pmatrix}1&0&0\\1&0&0\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]
Effect coding
カテゴリごとの重みは、対応するカテゴリと全体の平均 (他のすべての特徴がゼロまたは参照カテゴリである場合) の推定された y の差です。 最初の列は切片を推定するために用いられます。
切片に関連づけられた重み \(\beta_{0}\) は、全体の平均を表し、2 列目に対する重み \(\beta_{1}\) は、 全体の平均とカテゴリ B との間の差となります。 したがって、カテゴリ B の全体の効果は \(\beta_{0}+\beta_{1}\) となります。
カテゴリ C に対する解釈も同様です。 参照カテゴリ A に対しては、\(-(\beta_{1}+\beta_{2})\)が全体の平均を表し、\(\beta_{0}-(\beta_{1}+\beta_{2})\)が全体の影響となります。
Feature matrix:
\[\begin{pmatrix}1&-1&-1\\1&-1&-1\\1&1&0\\1&1&0\\1&0&1\\1&0&1\\\end{pmatrix}\]
Dummy coding
カテゴリごとの \(\beta\) は各カテゴリに対する推定された y の平均値です。(その他の特徴量はゼロもしくは、参照カテゴリ) ただし、切片は、線形モデルの重みに対して一意な解が見つけられるように、省略されていることに注意してください。
Feature matrix:
\[\begin{pmatrix}1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&0&1\\0&0&1\\\end{pmatrix}\]
カテゴリカル特徴量に対するエンコーディング手法にさらに興味がある場合は次のサイトをご覧ください。 概要サイト、 ブログ.
4.1.6 線形モデルは良い説明を与えるか?
人間に優しい説明の章で説明した、良い説明とは何かという観点で見ると、線形モデルは最良の説明を与えるというわけではありません。 これらは対照的ですが、参照インスタンスは全ての量的特徴量が0でありカテゴリカル特徴量は参照カテゴリであるようなデータ点となります。 これは大抵、現実的には起こりそうもない人工的で意味のないインスタンスです。
例外もあります: すべての量的特徴量が中心化(特徴量から特徴量の平均値を引いた値)されており、すべてのカテゴリ特徴量がエンコードされている場合、参照インスタンスは、すべての特徴量が平均値を取るデータ点となります。 これは実在しないデータ点かもしれませんが、少なくとも可能性が高く意味があるものかもしれません。 この場合、特徴量に重みを掛けたもの(feature effects)は、"平均的なインスタンス"と比較したときの予測結果への貢献度を説明しています。
良い説明のもう1つの側面は選択性であり、線形モデルにはおいては、より少ない特徴量を使うこと、もしくはスパースな線形モデルを用いることが挙げられます。 線形モデル自体では選択性を持つ説明は達成できないことに注意してください。
線形モデルは、線形方程式が特徴量と出力結果の関係を表す適切なモデルであるかぎり、正しい説明を与えます。 非線形性や交互作用が多いほど、線形モデルは正確ではなくなり、説明も真実味の欠如が起こります。 線形性はモデルに対する説明を、より一般的に単純にします。 人々が関係性を説明するために線形モデルを使う主な理由は、モデルの線形の性質によるものだと考えられます。
4.1.7 スパースな線形モデル
私が選んだ線形モデルの例は、どれも上手くいきましたよね? しかし実際のデータでは、ほんの一握りの特徴量ではなく、何百、何千の特徴量を持ってるかもしれません。 そのときに、線形回帰モデルはどうなるでしょうか。 解釈性は下がります。 インスタンスよりも特徴量が多く、標準的な線形モデルでは学習ができないという状況に陥ってしまうこともあるかもしれません。 このような時は、線形モデルにスパース性(=少数の特徴量)を導入することで解決できます。
4.1.7.1 Lasso
Lasso は、線形回帰モデルにスパース性を導入するための便利な方法です。 Lasso は「least absolute shrinkage and selection operator」の略で、線形回帰モデルに適用すると、特徴量の選択と選択された特徴量の重みの正則化を行います。 以下の重みを最適化する最小化問題を考えてみましょう。
\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_i^T\boldsymbol{\beta})^2\right)\]
Lasso は、この最適化問題に新しく項を付け加えます。
\[min_{\boldsymbol{\beta}}\left(\frac{1}{n}\sum_{i=1}^n(y^{(i)}-x_{i}^T\boldsymbol{\beta})^2+\lambda||\boldsymbol{\beta}||_1\right)\]
\(||\boldsymbol{\beta}||_1\) の項は、重みに対する L1 ノルムであり、大きな重みに対するペナルティの役割があります。 L1 ノルムを使用しているため、多くの重みは 0 となり、他の重みは小さくなります。 パラメータ \(\lambda\) は正則化効果の強さを制御し、通常はクロスバリデーションによって調整されます。 特に \(\lambda\) が大きいと、多くの重みが 0 になります。 特徴量の重みは、ペナルティ項 \(\lambda\) の関数として可視化できます。 各特徴量の重みは、次の図のように曲線で表すことができます。
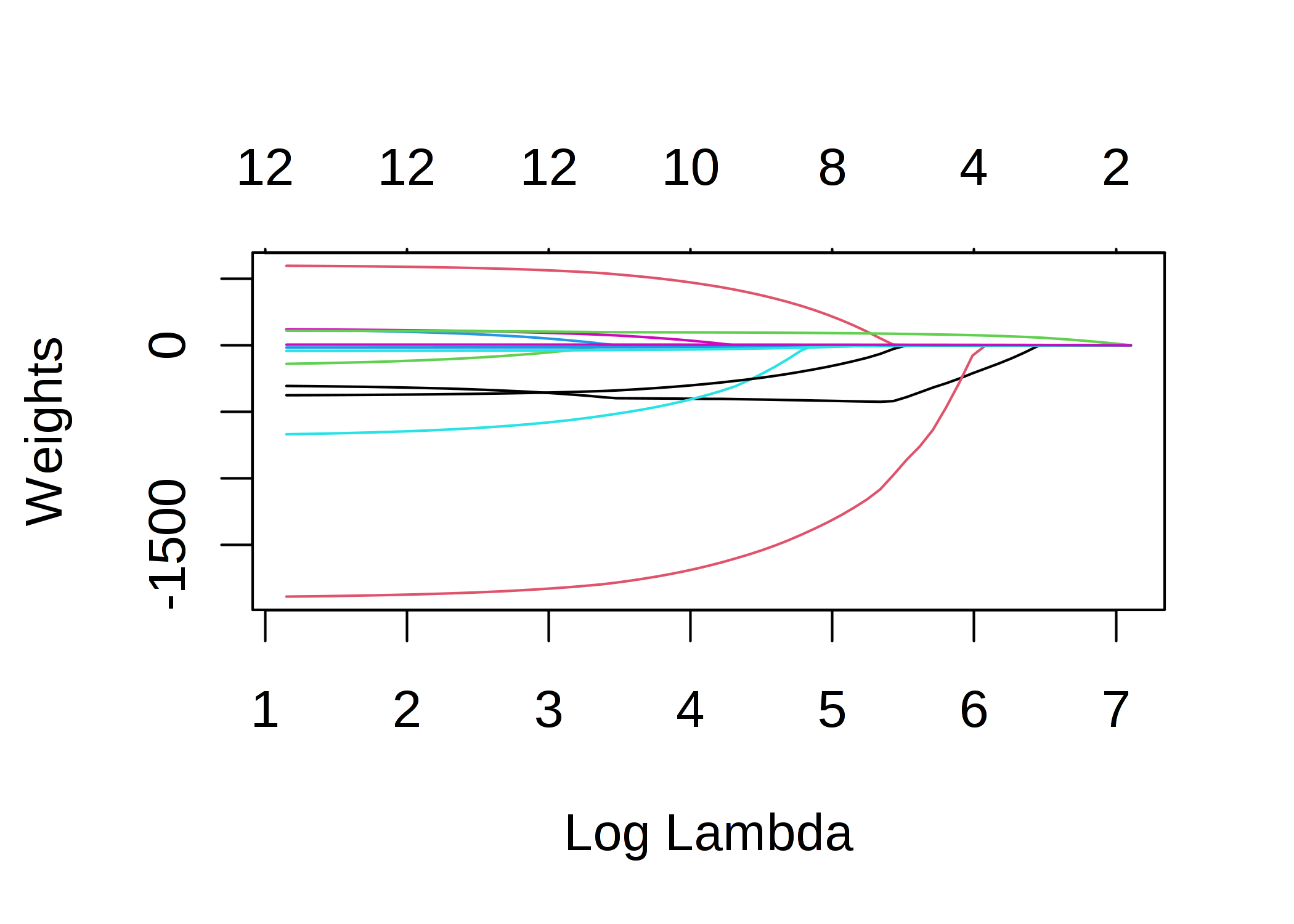
FIGURE 4.4: 重みに対するペナルティが大きくなるにつれて、非ゼロの重みを持つ特徴量が少なくなっていきます。これらの曲線は解パス図とも呼ばれます。プロットの上の数字は、非ゼロの重みの数です。
\(\lambda\) にはどのような値を選ぶべきでしょうか? ペナルティ項をチューニングできるパラメータとして捉えれば、クロスバリデーションでモデル誤差を最小化する \(\lambda\) を求めることができます。 \(\lambda\) をモデルの解釈性を制御するパラメータとして考えることもできます。 ペナルティが大きければ大きいほど、モデルに存在する特徴量が少なくなり(重みがゼロになるので)、モデルの解釈性が良くなります。
Lassoを使用した例
Lasso を使ってレンタル自転車の数を予測してみましょう。 モデルに持たせたい特徴量の数を事前に設定しておきます。 まずは特徴量の数を 2 に設定してみましょう。
| Weight | |
|---|---|
| seasonSPRING | 0.00 |
| seasonSUMMER | 0.00 |
| seasonFALL | 0.00 |
| seasonWINTER | 0.00 |
| holidayHOLIDAY | 0.00 |
| workingdayWORKING DAY | 0.00 |
| weathersitMISTY | 0.00 |
| weathersitRAIN/SNOW/STORM | 0.00 |
| temp | 52.33 |
| hum | 0.00 |
| windspeed | 0.00 |
| days_since_2011 | 2.15 |
Lasso により重みが 0 にならなかったのは2つの特徴量は、温度("temp")と時間トレンド("days_since_2011")です。
では、次に、5つの特徴量を選択してみましょう。
| Weight | |
|---|---|
| seasonSPRING | -389.99 |
| seasonSUMMER | 0.00 |
| seasonFALL | 0.00 |
| seasonWINTER | 0.00 |
| holidayHOLIDAY | 0.00 |
| workingdayWORKING DAY | 0.00 |
| weathersitMISTY | 0.00 |
| weathersitRAIN/SNOW/STORM | -862.27 |
| temp | 85.58 |
| hum | -3.04 |
| windspeed | 0.00 |
| days_since_2011 | 3.82 |
"temp" と "days_since_2011" の重みが、先に示した2つの特徴量を持つモデルとは異なることに注意してください。 この理由は、\(\lambda\) を減少させることで、2つの特徴量を持つモデルで選択された特徴量であっても、ペナルティが少なくなり、より大きな重みが得られる可能性があるからです。 Lasso の重みの解釈は、線形回帰モデルの重みの解釈に対応しています。 重みに影響するため、特徴量が標準化されているかどうかに注意を払う必要があります。 この例では、特徴量はソフトウェアによって標準化されていますが、重みは元の特徴量の尺度と一致するように自動的に変換されています。
線形モデルのスパース性のための他の方法
線形モデルの特徴量の数を減らすために、さまざまな手法があります。
前処理に関する方法
- 手動による特徴量選択: 専門家の知識・ドメイン知識を使うことで、特徴量の選択ができます。 自動化できないのが大きな欠点で、データを理解している人と協力する必要があります。
- 単変量選択: 例としては、相関係数があります。 特徴量と目的変数の相関関係が一定の閾値を超えた特徴量のみを選択します。 デメリットは、特徴量を単体でしか考えていないことです。 いくつかの特徴量は、線形モデルが他の特徴量を説明するまで相関を示さないかもしれません。 こういった場合、単変量選択法では見逃してしまいます。
段階的な方法
- Forward selection: 1つの特徴量で線形モデルをフィットします。 これを特徴量ごとに行います。 最も性能の良いモデルを選択してください (例: 決定係数 \(R^2\) が最大)。 ここでもう一度、残りの特徴量について、現在の最良のモデルに新たな特徴量を1つ追加することで、異なるバージョンのモデルを学習させます。 そして、最も性能の良いモデルを選びます。 この作業をモデル内の特徴量の最大数など、ある基準に達するまで続けましょう。
- Backward selection: この手法は Forward selection と似ています。 しかし、特徴量を追加するのではなく、すべての特徴量を含むモデルから始めて、どの特徴を削除すれば最高の性能向上が得られるかを試してみましょう。 これを、ある停止基準に達するまで繰り返します。
Lasso を使うことをお勧めする理由は、すべての特徴量を同時に考慮し、\(\lambda\) を変更することで制御できるからです。 また、Lassoは、分類のためのロジスティック回帰モデルでも使用できます。
4.1.8 長所
予測値を重み付き和としてモデル化することで、予測値がどのように生成されるかの透明性を高くできます。 そして、Lasso を使用することで、使用される特徴量の数を減らすことができます。
多くの人が線形回帰モデルを使います。 これは、多くの場所で、予測モデルや推論実行のために線形モデルが受け入れられていることを意味します。 線形回帰に関して、高度な経験をもつ専門家がいたり、教材やソフトウェアなども豊富にあります。 線形回帰はR、Python、Java、Julia、Scala、Javascript、その他多数で使用できます。
数学的には、重みを推定するのは簡単で、最適な重みを見つけることができることが保証されています(線形回帰モデルのすべての仮定がデータによって満たされている場合)。
重みと一緒に、信頼区間、検定、強固な統計理論を得ることができます。 線形回帰モデルの拡張もたくさん知られています(GLM,GAMなどの章を参照)。
4.1.9 短所
線形回帰モデルは、線形関係しか表現できません。 非線形性や交互作用を考慮するには、手作業で新たに特徴量を作成する必要があります。
線形モデルは、学習できる関係が非常に制限されており、実際には複雑な関係を単純化しすぎているため、予測性能に関してもあまり良くないことが多いです。
重みの解釈は、他のすべての特徴量に依存しているため、直感的ではない場合があります。 出力 y と他の特徴量に対して強い正の相関のある特徴量は、線形モデルにおいては、負の重みとなる可能性があります。なぜなら、他にも相関のある特徴量がある場合、高次元空間において y と負の相関があるためです。 完全に相関のある特徴量がある場合は、線形方程式の一意の解を見つけることが不可能になります。
例: 家の価値を予測するモデルがあり、部屋数や広さなどの特徴量があります。 家の大きさと部屋の数は非常に強い相関関係があります。つまり、家が大きければ大きいほど、部屋数が多くなります。 線形モデルに両方の特徴量を使用した場合、家のサイズがより良い予測指標となり、大きな正の重みを取得することが起こるかもしれません。 そうすると、同じ広さの家でも、部屋数を増やすと価値が下がったり、相関関係が強すぎると線形方程式が安定しなくなったりするので、部屋の数に対する重みは負になるかもしれません。
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. "The elements of statistical learning". www.web.stanford.edu/~hastie/ElemStatLearn/ (2009).↩