5.8 Scoped Rules (Anchors)

著者: Tobias Goerke & Magdalena Lang

This chapter is currently only available in this web version. ebook and print will follow.

Anchor は、予測を "固定" するのに十分な決定規則を見つけることにより、ブラックボックスの分類モデルの個々の予測結果を説明します。 他の特徴量の値が変わっても予測に影響がない場合、ルールにより予測は固定されます。 Anchor は、強化学習とグラフ探索アルゴリズムを組み合わせて、モデルの呼び出し回数を最小限に抑えながら（これにより実行時間も抑えられます）、局所最適解に陥るのを回避できます。 このアルゴリズムは、2018年に Ribeiro、Singh、Guestrinら38により提案されました (LIMEアルゴリズムを導入したのも彼らです)。

LIME と同様に、Anchor は、ブラックボックスな機械学習モデルの予測に対して 局所的な 説明をするためにデータに 摂動 を与える方法を採用しています。 ただし、LIME が説明のためにサロゲートモデルを用いるのに対し、Anchor では Anchor と呼ばれる、より理解しやすい IF-THEN ルールが用いられます。 これらのルールはスコープ化されているので再利用が可能です。つまり、Anchor はカバレッジの概念が含まれており、それが他のインスタンス、もしくはまだ見ぬインスタンスに適用されるかを正確に示しています。 Anchor を見つけることは、強化学習の分野に由来する探索または多腕バンディット問題を伴います。 そのため、説明される各インスタンスに対して、近傍データ（摂動）を作成し、評価する必要があります。 そうすることで、ブラックボックスの構造とその内部パラメータを無視するアプローチが可能になり、これらが参照されず、変更されないままになります。 したがって、このアルゴリズムは モデル非依存 であり、任意の クラスのモデルに適用できます。

彼らの論文では、LIME と Anchor の両方のアルゴリズムを比較し、結果を導出するためにインスタンスの近傍を参照する方法がどのように異なるかを視覚化しています。 次の図は、2つのインスタンスを使用して、LIME と Anchor の両方が複雑な2値分類モデル（- または + のいずれかを予測）を局所的に説明している様子を示しています。 LIMEは、摂動空間 \(D\) が与えられたモデルを局所的に最もよく近似する線形決定境界を学習するだけなので、LIMEの結果がどれだけ忠実であるかを示すものではありません。 同じ摂動空間を与えられると、Anchor は、モデルの振る舞いに適応したカバレッジを持つ説明を構築し、その境界を明確に表現します。 したがって、Anchor は設計上忠実であり、どのインスタンスに対して有効であるかを正確に示します。 この特性により、Anchor は特に直感的で理解しやすくなります。

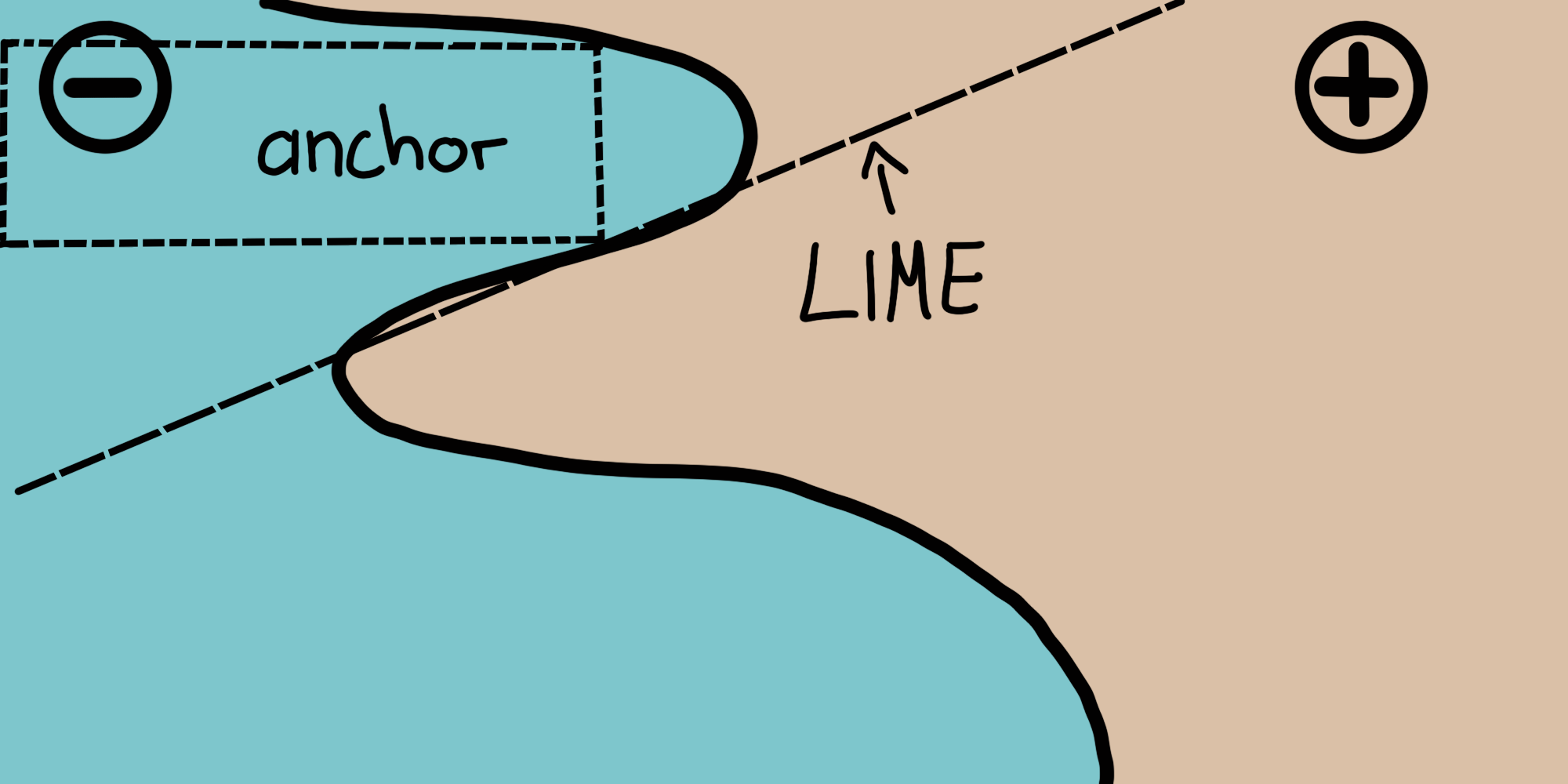
LIME vs. Anchor -- 簡単な可視化。図はRibeiro, Singh, and Guestrin (2018)より

FIGURE 5.36: LIME vs. Anchor -- 簡単な可視化。図はRibeiro, Singh, and Guestrin (2018)より

前述したように、アルゴリズムの結果や説明は、Anchor と呼ばれるルールの形で得られます。 例えば、タイタニック号の事故で乗客が生き残るかどうかを予測する二変量のブラックボックスモデルが与えられたとします。 ここで私たちは、モデルがある特定の個人の生存を予測している 理由 を知りたいと思います。 Anchor アルゴリズムは、以下に示すような説明を提供します。

表 ある個人とモデルの予測の例。

Feature Value
Age 20
Sex female
Class first
TicketPrice 300$
More attributes ...
Survived true

そして、対応するAnchorsの説明は以下のようになります。

IF SEX = female
AND Class = first
THEN PREDICT Survived = true
WITH PRECISION 97%
AND COVERAGE 15%

この例は、Anchor がモデルの予測についての本質的な洞察とその基礎となる根拠を提供できることを示しています。 結果は、モデルがどの属性を考慮に入れたかを示しており、この例では女性でありファーストクラスであることが考慮されていました。 人は正確さを最優先するため、このルールを使ってモデルの振る舞いを検証できます。 Anchor によると、このルールは摂動空間のインスタンスの 15% に適用できます。 その場合の説明は 97％ の確率で正確であり、表示された述部が予測された結果のほぼ唯一の原因であることを意味しています。

Anchor \(A\) は正式には次のように定義されます。

\[\mathbb{E}_{\mathcal{D}_x(z|A)}[1_{f(x)=f(z)}]\geq\tau,A(x)=1\]

  • \(x\) は説明されるインスタンス（例えば、表形式のデータセットの1行）を表します。
  • \(A\) は述部の集合、すなわち結果のルールまたは Anchor を示します。すべての \(x\) の特徴量の値が \(A\) によって定義された特徴量の述部に対応するとき、\(A(x)=1\) となります。
  • \(f\) は、説明する分類モデル（例えば、ニューラルネットワークモデル）を表します。これは、\(x\) とその摂動に対するラベルを予測できる必要があります。
  • \(D_x　(\cdot|A)\) は、\(A\) に一致する \(x\) の近傍データの分布を示しています。
  • \(0 \leq \tau \leq 1\) は精度の閾値を指定します。少なくとも \(\tau\) 以上の局所的な忠実性 (local fidelity)を達成したルールのみが有効な結果とみなされます。

形式的な説明は威圧的かもしれないので、言葉にしてみましょう。

説明されるインスタンス \(x\) が与えられると、\(x\) に適用されるようなルールまたは Anchor \(A\) を見つけます。このとき、同じ \(A\) を適用できる \(x\) の近傍データのうち、少なくとも \(\tau\) の割合 については \(x\) と同じクラスであると予測されるようにします。ルールの精度は、与えられた機械学習モデル（指標関数 \(1_{f(x) = f(z)}\) で示される）を用いて、近傍データまたは摂動（\(D_x (z|A)\) に続く）を評価することで得られます。

5.8.1 Anchor の発見

Anchor の数学的な説明は明確で分かりやすいように見えますが、特定のルールを作成することは実行不可能です。 すべての連続空間や大規模な入力空間では不可能な \(z \in \mathcal{D}_x(\cdot|A)\) で \(1_{f(x) = f(z)}\) を評価する必要があります。 それゆえ、著者らは \(0 \leq \delta \leq 1\) のパラメータを使用して、確率的な定義をします。 このようにして、サンプルは統計的に信頼のある精度が出るまで引き出されます。 確率的な定義は以下のようになります。

\[P(prec(A)\geq\tau)\geq{}1-\delta\quad\textrm{with}\quad{}prec(A)=\mathbb{E}_{\mathcal{D}_x(z|A)}[1_{f(x)=f(z)}]\]

前述の2つの概念はカバレッジの概念により結合・拡張されます。 その理論的根拠はモデルの入力空間の大部分に適用できるルールを見つけることから構成されます。 カバレッジは近傍(摂動空間)に適応できる Anchor の確率として定義されます。

\[cov(A)=\mathbb{E}_{\mathcal{D}_{(z)}[A(z)]}\]

この要素を含めるとカバレッジ最大化を考慮できる Anchor の最終的な定義が可能となります。

\[\underset{A\:\textrm{s.t.}\;P(prec(A)\geq\tau)\geq{}1-\delta}{\textrm{max}}cov(A)\]

したがって、この手続きではすべての適格なルール（確率的な定義の閾値を満たす全てのルール）の中で最大のカバレッジをもつルールを目指しています。 モデルの大部分を説明するために、これらのルールはより重要なものと考えられます。 ただし、より多くのルールを持つ述部は、ルールが少ないときと比べて精度が高くなることに注意してください。 特に、\(x\) のそれぞれの特徴量を固定するようなルールは、評価する近傍を同一のインスタンスのみに減らします。 それゆえ、モデルは全ての近傍を同様に分類し、規則の精度は \(1\) になります。 同時に、多くの特徴を固定するルールは、特定のしすぎであり、少数のインスタンスにしか適用できません。 それゆえ、 精度とカバレッジにはトレードオフ があります。

Anchor のアプローチは説明を見つけるため、下図のように、4つの要素を使用します。

候補の生成: 説明の候補を生成します。 最初の段階では、\(x\) のそれぞれの特徴量に対して1つの候補が作成され、可能な摂動の値でそれぞれの値を固定します。 その他の段階では、前の段階での最良な候補に、まだ含まれていない述語を1つ追加することで拡張されます。

最良の候補の特定: 候補となるルールのうち、どのルールが \(x\) を最も説明できているか比較できる必要があります。 この目的を達成するために、現在観測されているルールに合う摂動が作成され、モデルを呼び出すことで評価されます。 しかしながら、これらの呼び出しは計算負荷を少なくするために最小限にする必要があります。 そのため、この要素の中核には純粋な探索問題 Multi-Armed-Bandit（MAB; 正確には KL-LUCB39）があります。 MAB は逐次選択を使用して、様々な戦略 (スロットマシーンに倣ってアームと呼ばれる) を効率的に探索するために使用されます。 与えられたルールの中では、それぞれの候補となるルールはアームに見立てられます。 アームが引っ張られるたびに、それぞれの近傍が評価され、候補のルールの報酬についてより多くの情報（Anchor の場合の精度）を得ることができます。 精度はルールがどの程度インスタンスを説明できているかを示します。

候補の精度検証: 候補の精度が閾値 \(\tau\) を超えているかどうか統計的に信頼性がない時はさらに多くのサンプルを取ります。

修正されたビームサーチ: 上記全ての要素はグラフ探索アルゴリズムで幅優先アルゴリズムの派生であるビームサーチによって組み立てられます。 ビームサーチは各ラウンドの \(B\) 個の最良の候補を次のラウンドに運びます (\(B\) は ビーム幅 と呼ばれます)。 これらの \(B\) 個の最良のルールは次の新しいルールを作るために使用されます。 ビームサーチは各特徴量が含まれるのは1回だけなので最大で \(featureCount(x)\) 回行います。 それゆえ、それぞれのラウンド \(i\) で、それぞれ \(i\) 個の述語をもつ候補を生成してその中で最良の \(B\) 個を選択します。 したがって、\(B\) を高く設定するとアルゴリズムは局所最適解を回避しやすくなります。 一方で、モデルの呼び出し回数は多くなるため、計算負荷が増加します。

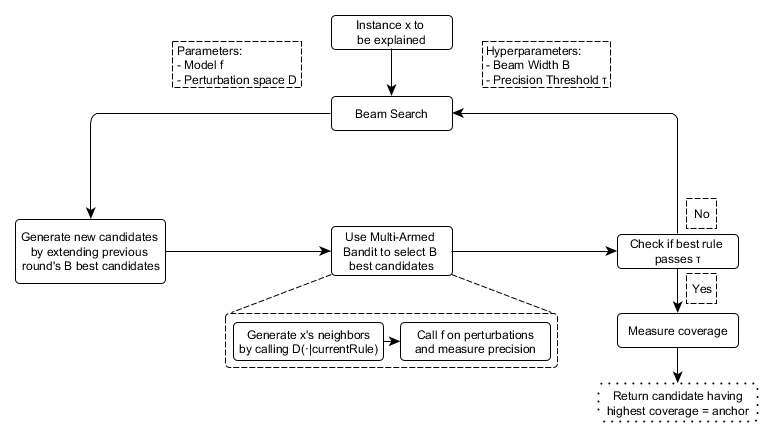
Anchor アルゴリズムの構成要素とその相互関係（簡易版）

FIGURE 5.37: Anchor アルゴリズムの構成要素とその相互関係（簡易版）

このアプローチは一見すると、どのようなシステムでもインスタンスを分類した理由について、統計的に健全な情報を効率的に導き出すことができる完璧なレシピのように見えます。 このアプローチは、モデルの入力を機械的に実験し、それぞれの出力を観察することで結論づけます。 モデルの呼び出し回数を削減するために、研究・確立された機械学習の手法（MAB）に依存します。 これによりアルゴリズムの時間を短縮できます。

5.8.2 複雑性と実行時間

Anchor アプローチの漸近的な実行時間のふるまいを知ることは、特定の問題に対してどのくらい良いパフォーマンスが期待されるかを評価することに役立ちます。 \(B\) はビーム幅、\(p\) は特徴量の数とします。 すると、Anchor アルゴリズムは次のようになります。

\[\mathcal{O}(B\cdot{}p^2+p^2\cdot\mathcal{O}_{\textrm{MAB}\lbrack{}B\cdot{}p,B\rbrack})\]

この境界は統計的な信頼度 \(\delta\) のような、問題に依存しないハイパーパラメータを抽象化したものです。 ハイパーパラメータを無視することで、境界の複雑さを軽減できます (詳細は元の論文を参照してください)。 MABは各ラウンドで \(B \cdot p\) の中から最良の候補 \(B\) を取り出すので、ほとんどのMABとその実行時間は、他のパラメータに係数 \(p^2\) がかけられます。

ですからこれは明らかなことですが、特徴量が大きくなると、アルゴリズムの効率は低下します。

5.8.3 表形式データの例

表形式のデータは表によってあらわされた構造化データで、列は特徴量を表し、行はインスタンスを表しています。 Anchor アプローチのポテンシャルを示すために、例として、レンタル自転車のデータを使って、選択されたインスタンスの機械学習の予測の説明をしてみましょう。 ここでは、回帰ではなく分類問題として扱い、ブラックボックスモデルとしてランダムフォレストで学習しています。 レンタル自転車の数がトレンド曲線よりも上にあるか下にあるかを分類しています。

Anchor による説明を生成する前に、摂動関数を定義する必要があります。 簡単な方法としては、例えば学習データからサンプリングして作られた直感的な摂動空間を用いることです。 インスタンスを摂動させるとき、このデフォルトのアプローチでは、Anchor の述語の対象となる特徴量の値を維持し、固定されていない特徴量を、特定の確率でランダムにサンプリングされた別のインスタンスの値で置き換えます。 このプロセスでは、説明されるインスタンスと似ているが、他のランダムなインスタンスの値もいくつかもつような新たなインスタンスを生成します。 このようなインスタンスは、近傍と言えます。

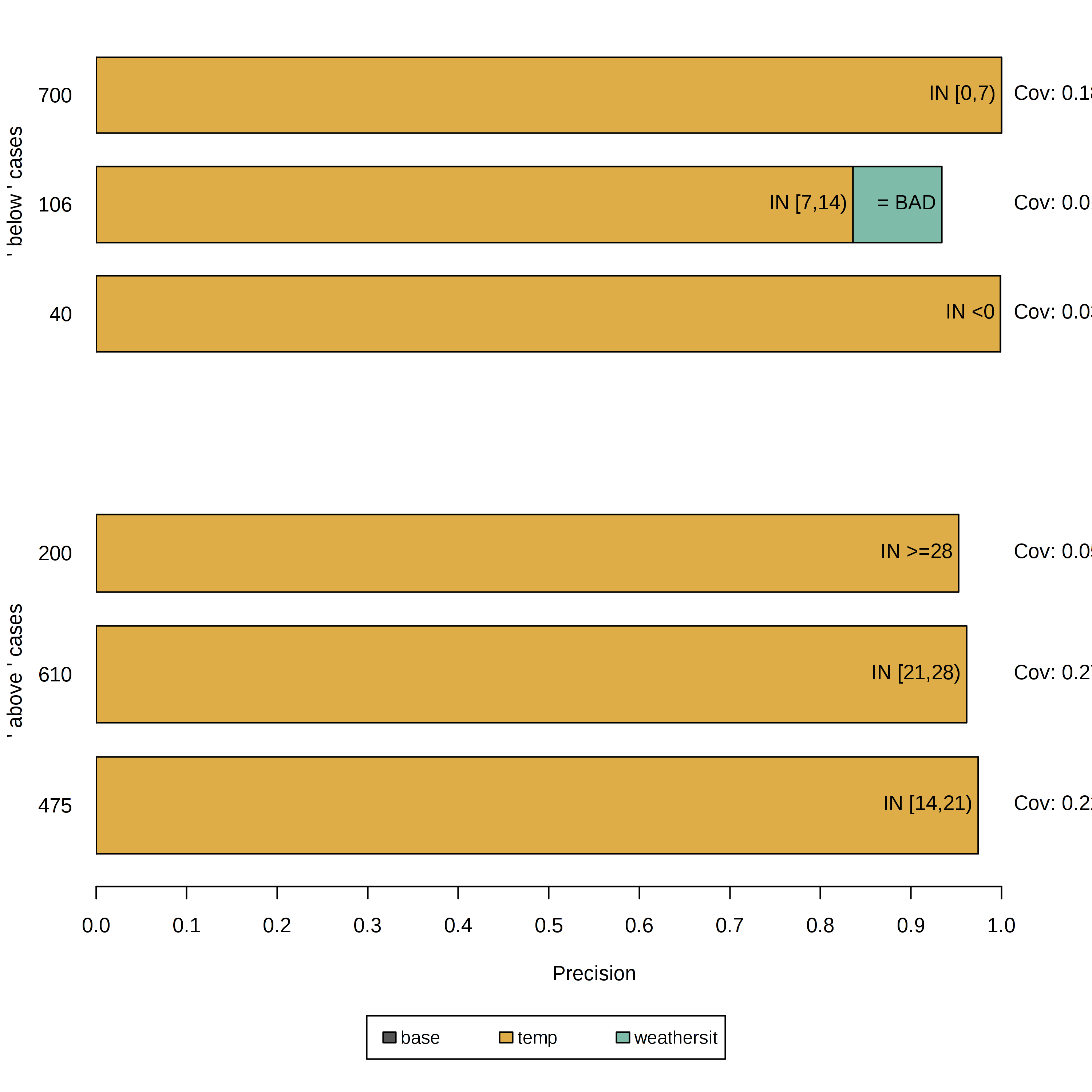
レンタル自転車のデータセットの6つのインスタンスを説明する Anchor。各列は1つの説明もしくはAnchor、各バーはそれに含まれた特徴量の述部を表している。x軸はルールの精度を表し、バーの厚みは範囲に対応している。'base' ルールは述部を含んでない。これらの Anchor によってモデルは予測の際に主に温度を考慮に入れていることが示されている。

FIGURE 5.38: レンタル自転車のデータセットの6つのインスタンスを説明する Anchor。各列は1つの説明もしくはAnchor、各バーはそれに含まれた特徴量の述部を表している。x軸はルールの精度を表し、バーの厚みは範囲に対応している。'base' ルールは述部を含んでない。これらの Anchor によってモデルは予測の際に主に温度を考慮に入れていることが示されている。

この結果は直感的に解釈できるもので、モデルの予測に関してどの特徴量が最も重要であるかがそれぞれのインスタンスについて示されています。 さらに、Anchorは少ない述部しか持たないので、広い範囲をカバーし他のケースにも適用できます。 上に示されるルールは \(\tau = 0.9\) で作成されました。 つまり、評価された摂動が \(90\%\) の精度でラベルを忠実にサポートするような Anchor が求められます。 また、量的特徴量の表現力や適応性を上げるために離散化も行っています。

これまでのすべてのルールは、モデルが少ない特徴量に基づいて自信を持って決定できるインスタンスに対して 作られました。 しかし、他のインスタンスはより多くの特徴量が重要であるため、モデルによって明確に分類されていません。 そのような場合には、Anchor はより具体的になり、より多くの特徴量を持ち、より少ないインスタンスにのみ適用されます。

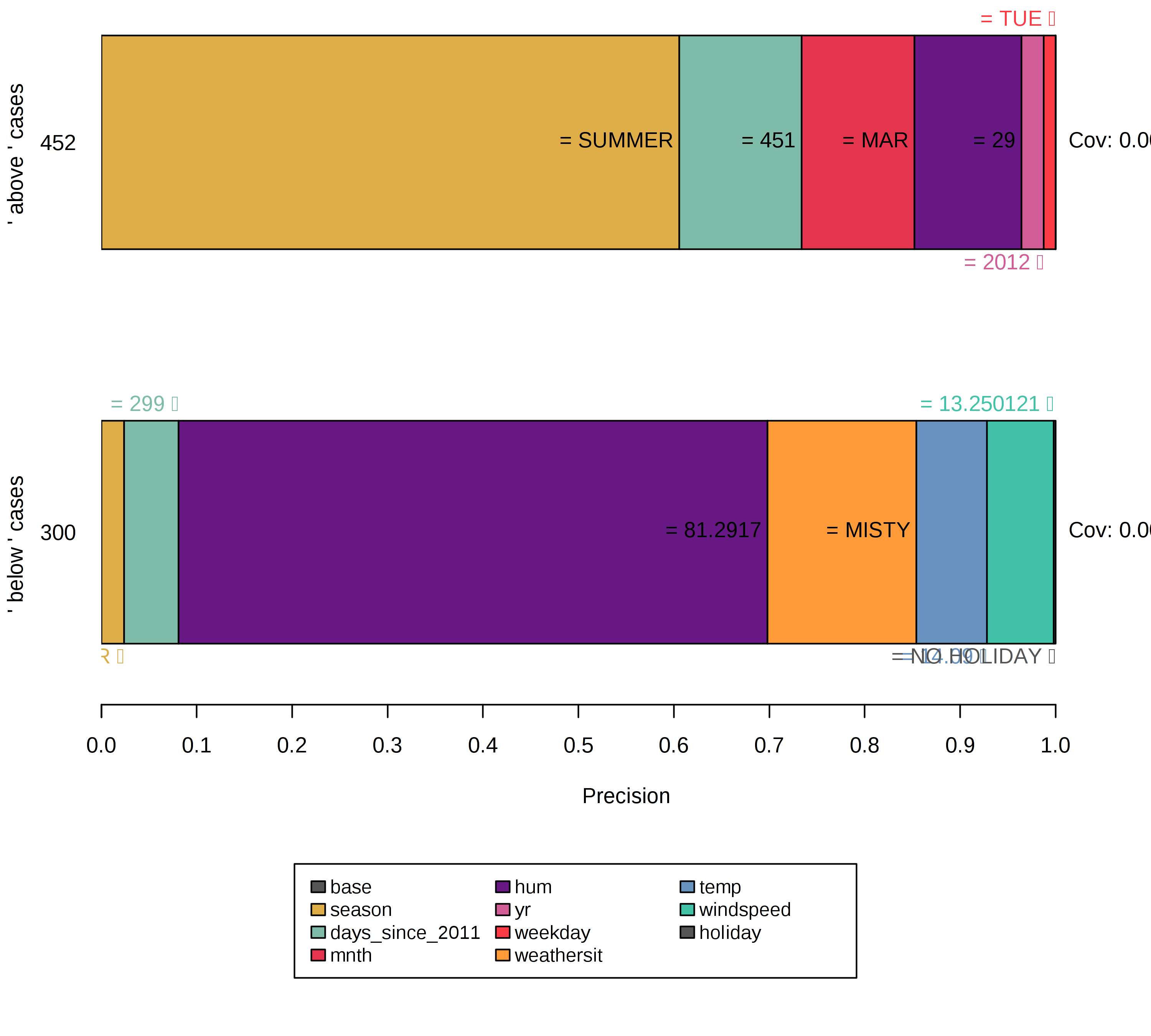
決定境界周辺のインスタンスを説明するには、より多くの特徴量の述部とより低いカバレッジからなる特殊なルールが必要。空のルール、すなわち基本特徴量は重要性が低くなる。これは、インスタンスが不安定な近傍の中に位置するので、決定境界のシグナルとして解釈できる。

FIGURE 5.39: 決定境界周辺のインスタンスを説明するには、より多くの特徴量の述部とより低いカバレッジからなる特殊なルールが必要。空のルール、すなわち基本特徴量は重要性が低くなる。これは、インスタンスが不安定な近傍の中に位置するので、決定境界のシグナルとして解釈できる。

デフォルトの摂動空間を選ぶことは適した選択ですが、一方でアルゴリズムに大きな影響を与え、結果が偏ってしまう可能性もあります。 例えば、学習データが不均衡である（それぞれのクラスのインスタンスの数が均等でない）とき、摂動空間も同様になります。 さらにこの状況はルールの発見や結果の精度にも影響します。

子宮頸がんのデータセットは Anchor アルゴリズムが以下のような状況につながる典型的な例です。

  • healthy とラベル付けされたインスタンスはすべての近傍が healthy と評価されるので空のルールが作り出されます。
  • 摂動空間はほとんどが healthy データの値でカバーされているため、cancer とラベル付けされたインスタンスに対する説明は過度に具体的であり、述部は多くの特徴量を持っています。
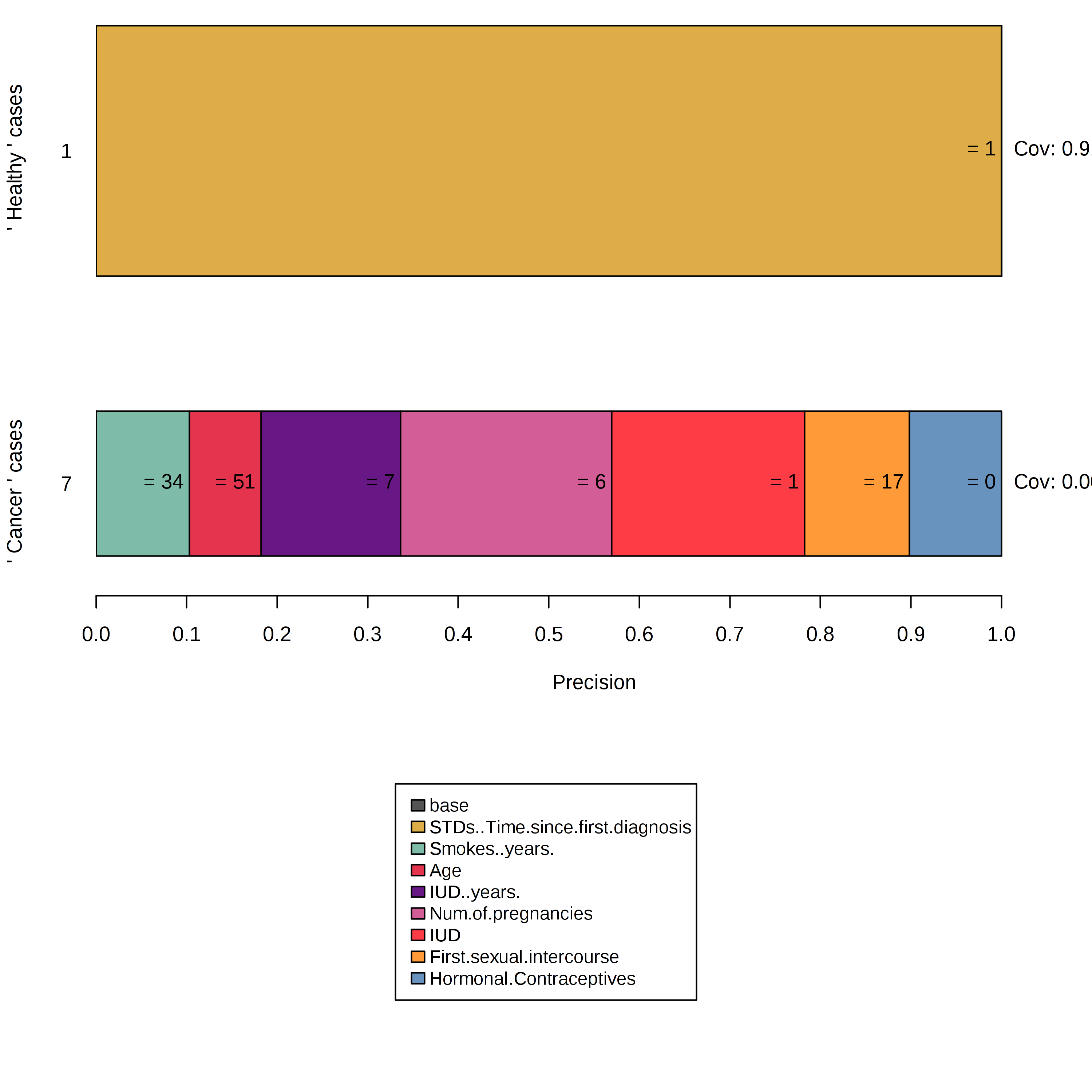
不均衡な摂動空間中で Anchor を構築すると、予期しない結果となる。

FIGURE 5.40: 不均衡な摂動空間中で Anchor を構築すると、予期しない結果となる。

この結果は、求めていたものとは異なるでしょうが、いくつかの方法でアプローチできます。 例えば、不均衡なデータセットや正規分布から異なるサンプリング方法で得られる別の摂動空間を定義できます。 しかし、これには副作用があります。それは、サンプリングされた近傍は代表的なものでなく、カバレッジのスコープが変わってしまいます。 あるいは、MAB の信頼度 \(\delta\) と誤差パラメータの値 \(\epsilon\) を修正するという方法もあります。 これによって MAB はより多くのサンプルを引き出し、最終的にマイノリティのサンプルが、よりサンプリングされやすくなります。

例えば、多くのケースが cancer とラベル付けされているように子宮頸がんデータの一部のみを使用します。 そして、そこから対応する摂動空間を作るようなフレームワークを使用します。 摂動は、予測を変化させる可能性が高くなり、Anchor アルゴリズムは重要な特徴量を特定できるようになります。 しかし、カバレッジの定義を考慮に入れる必要があり、カバレッジは摂動空間の中でのみ定義されています。 前の例では、摂動空間の基底として学習データを用いました。 ここではデータセットの一部を用いているので、カバレッジが高いことは必ずしもグローバルにルールの重要性が高いことを示しているわけではありません。

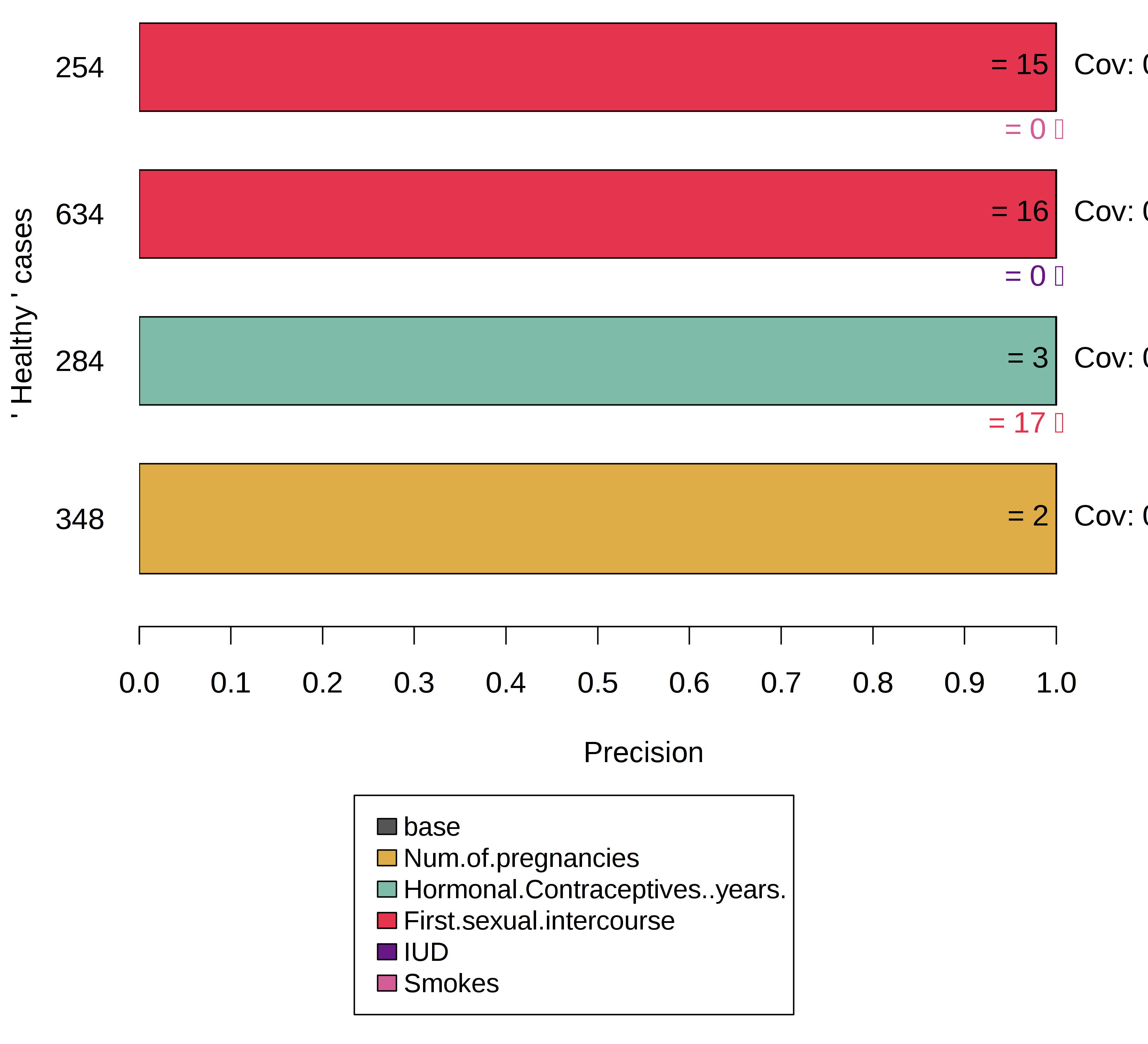
Anchor を構築する前にデータセットを均一にすることで、マイノリティのケースにおけるモデルの判断根拠がわかる。

FIGURE 5.41: Anchor を構築する前にデータセットを均一にすることで、マイノリティのケースにおけるモデルの判断根拠がわかる。

5.8.4 長所

Anchor のアプローチは、LIME に比べて複数の長所があります。 まず第一に、ルールが 解釈しやすい ため（素人であっても）、アルゴリズムの出力を容易に理解できます。 さらに、Anchor はサブセット化可能 であり、カバレッジの概念を含めることで重要度の尺度を示します。 第二に、Anchor のアプローチは入力の近傍において モデルによる予測が非線形や複雑な場合でも機能します。 このアプローチはサロゲートモデルをフィッティングする代わりに強化学習の手法を使用するため、モデルのアンダーフィットは起こりにくいです。

それとは別に、アルゴリズムがモデルに依存しないため、どのモデルに対しても適用できます。 さらに、アルゴリズムはバッチサンプリングをサポートしているMAB（BatchSARなど）を利用することで並列化できるので、非常に効率的です。

5.8.5 短所

このアルゴリズムは、ほとんどの摂動ベースの説明手法と同様に、高度に変更可能で影響力のある設定に悩まされます。 意味のある結果を得るために、ビーム幅や精度の閾値などのハイパーパラメータを調整する必要があるだけでなく、摂動関数を1つのドメイン／ユースケース用に設計する必要もあります。 表形式のデータをどのように摂動させるか考えてみてください。 同様の摂動を画像データに適用するにはどうしたらいいでしょうか（ヒント: 適用できません）。 幸いなことに、一部のドメイン（表形式など）ではデフォルトのアプローチが使用され、説明の初期設定が楽になります。

また、多くの場合では離散化が必要です。 そうしないと、結果が具体的すぎたり、カバレッジが低すぎたり、モデルの理解に貢献しないものになってしまうからです。 離散化は役立つ場合もありますが、不用意に使用すると決定境界が曖昧になる可能性があり、全く逆の効果をもたらしてしまいます。 最良の離散化手法は存在しないため、悪い結果が得られないように、ユーザはデータの離散化手法を決定する前にデータを把握する必要があります。

Anchor の構築には、全ての摂動ベースの説明手法と同様に、機械学習モデルを何度も呼び出す 必要があります。 アルゴリズムは呼び出し回数を最小限に抑えるために MAB を使用していますが、それでも実行時間はモデルのパフォーマンスに大きく依存するため非常に変わりやすいです。

最後に、一部のドメインではカバレッジの概念が定義されていません。 例えば、ある画像のスーパーピクセルと他の画像のスーパーピクセルをどのように比較するのか、その明確なまたは普遍的な定義はありません。

5.8.6 ソフトウェアと代替手法

現在、Python パッケージの anchor（Alibiにも統合されています）と Java implementation の2つの実装が利用可能です。 前者は Anchor アルゴリズムの著者のリファレンスで、後者は高い性能を示す R のインターフェイスを持つ実装であり、anchorsと呼ばれています。 この章の例ではこれを用いました。 今のところ、Anchor は表形式のデータのみをサポートしています。 ただし、理論的には任意のドメインまたはデータのタイプに対しても使うことができます。

  1. Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin. "Anchors: High-Precision Model-Agnostic Explanations." AAAI Conference on Artificial Intelligence (AAAI), 2018↩

  2. Emilie Kaufmann and Shivaram Kalyanakrishnan. “Information Complexity in Bandit Subset Selection”. Proceedings of Machine Learning Research (2013).↩