5.4 特徴量の相互作用

予測モデルにおいて特徴量の相互作用がある場合、ある特徴量は他の特徴量の値に影響を受けるため、予測は単に特徴量の影響の和では表現できなくなります。アリストテレスは「全体は部分の総和より勝る」という言葉を残しましたが、これも相互作用の存在により成り立つといえるでしょう。

5.4.1 特徴量の相互作用とは

機械学習モデルが2つの特徴量に基づいて予測する場合、この予測は定数項、1つ目の特徴量、2つ目の特徴量、2つの特徴量の相互作用の4つの項に分解できます。 2つの特徴量の相互作用は個々の特徴量の効果を考慮したのち、特徴量を変化させることによって生じる予測の変化を指します。

例として、モデルが家の大きさ（大きいか小さいか）と家の立地（良いか悪いか）の2つを特徴量として家の価値を予測する場合を考えると、以下のような4つの予測が考えられます。

立地	大きさ	予測
良い	大きい	300,000
良い	小さい	200,000
悪い	大きい	250,000
悪い	小さい	150,000

この予測結果は定数項 (150,000）、家の大きさ（大きければ+100,000、小さければ+0）、家の立地（よければ+50,000、悪ければ+0）のように分解できます。この分解はモデルの予測を完璧に説明しています。モデルの予測は大きさと立地の各特徴量の影響の和と等しくなっているため、相互作用による影響はありません。小さな家から大きな家に変更した場合、予測は立地に関わらず100,000だけ上がり、同様に立地を悪い家から良い家に変更した場合も、予測は家の大きさに関わらず50,000だけ増加します。

次に、相互作用が存在する場合について考えます。

立地	大きさ	予測
良い	大きい	400,000
良い	小さい	200,000
悪い	大きい	250,000
悪い	小さい	150,000

この予測結果を定数項 (150,000）、家の大きさ（大きければ+100,000、小さければ+0) 、家の立地 (よければ+50,000、悪ければ+0) のように分解してみます。ただし、今回は相互作用による項 (家のサイズが大きくかつ立地が良いならば+100,000) を追加で考える必要があります。この場合、立地によって、家が大きい場合と小さい場合で予測に差が生じるため、家の大きさと立地の間に相互作用があると言えます。

相互作用の大きさを測る1つの方法として、特徴量の相互作用により予測がどの程度変化するかを測る方法があります。これは H 統計量と呼ばれ、Friedman と Popescu によって2008年に提案されました³¹。

5.4.2 Friedman の H統計量の理論

これから、2つのケースについて扱います。 1つ目は、モデル内の2つの特徴が相互作用するかどうかや、その程度を示す双方向相互作用の尺度です。 2つ目は、ある特徴量がモデル内で他の全ての特徴量と相互作用するかどうかやその程度を示す総合的な相互作用の尺度です。理論的には、任意の数の特徴量間の相互作用を測定できます。しかし、上記の2つが最も興味深いケースです。

もし2つの特徴量が相互作用しない場合、partial dependence function として、以下のように分解できます (ただし、partial dependence function はゼロに中心化されていると仮定) 。

\[PD_{jk}(x_j,x_k)=PD_j(x_j)+PD_k(x_k)\]

ここで、 \(PD_{jk}(x_j,x_k)\) は2つの特徴量に関する2方向の partial dependence function であり、\(PD_j(x_j)\) と \(PD_k(x_k)\) は1つの特徴量についてのpartial dependence functionです。

同様に、もしも1つの特徴量が他のいかなる特徴量とも相互作用しない場合、予測関数 \(\hat{f}(x)\) を partial dependence function の和として表現できます。ここで、和の第1項は j にのみ依存し、第2項は j 以外に依存します。

\[\hat{f}(x)=PD_j(x_j)+PD_{-j}(x_{-j})\]

ただし、\(PD_{-j}(x_{-j})\) はj番目を除いた全ての特徴量に依存する partial dependence function です。

この分解は、(特徴量 j と k、もしくは、特徴量 j とその他に) 相互作用のない partial dependence function (もしくは完全予測関数) を表します。次のステップとして、観測された partial dependence function と相互作用を持たない分解された関数の差を測定します。 2つの特徴間の相互作用を測るための partial dependence function や、ある特徴量とそれ以外の間の相互作用を測るための関数全体の出力のばらつきを計算します。

相互作用 (観測値と理論的な相互作用のない状態のPDの差分)による因子寄与の量が、相互作用の強さを示す統計量として用いられています。相互作用が何もない場合、統計量は 0 であり、 \(PD_{jk}\) もしくは \(\hat{f}\) の全ての分散がpartial dependence functionの合計によって説明される場合は1になります。相互作用の統計量が 1 のとき、2つの特徴量のそれぞれの PD function は定数で、予測の影響が相互作用のみであることを意味しています。この H 統計量は 1 よりも大きくなることがあり、解釈がより困難になります。これは、双方向相互作用の分散が2次元の partial dependence plot の分散よりも大きい場合に起こる可能性があります。

数学的には、特徴量 j, k 間の H 統計量は Friedman と Popescu によって与えられ、以下の式で書き表されます。

\[H^2_{jk}=\sum_{i=1}^n\left[PD_{jk}(x_{j}^{(i)},x_k^{(i)})-PD_j(x_j^{(i)})-PD_k(x_{k}^{(i)})\right]^2/\sum_{i=1}^n{PD}^2_{jk}(x_j^{(i)},x_k^{(i)})\]

特徴量 j とそれ以外の全ての特徴量との相互作用を測るのも同様にして以下の通りに計算できます。

\[H^2_{j}=\sum_{i=1}^n\left[\hat{f}(x^{(i)})-PD_j(x_j^{(i)})-PD_{-j}(x_{-j}^{(i)})\right]^2/\sum_{i=1}^n\hat{f}^2(x^{(i)})\]

全てのデータ点で反復し、それぞれのデータ点で partial dependence を評価する必要があるため、H 統計量は評価にはコストがかかります。最悪のケースでは、双方向H統計量 (j vs. k) を計算するために、2n² 回の機械学習モデルの予測を呼び出す必要があり、全てのH統計量 (j vs. all) を計算するためには、3n² 回必要になります。計算を高速化するために、n 個のデータ点をサンプリングする方法があります。この方法は partial dependence の推定のばらつきを高めてしまう欠点があるため、これによって H 統計量は不安定になります。従って、もしも計算負荷を減らすためにサンプリングを用いている場合は、十分なデータ点が取得できているか注意してください。

Friedman と Popescu は、H統計量が0と有意に異なるかどうかを評価するための検定も提案しています。この場合の帰無仮説は、「相互作用がない」です。帰無仮説の下で相互作用統計量を生み出すには、モデルを調整して特徴量 j と k 、もしくは j と他の全ての特徴量との間に相互作用が無いようにする必要がありますが、これは任意のモデルのタイプで行えるわけではありません。よって、この検定はモデル非依存ではなく、モデル特有のものなのでここでは扱いません。

もしも予測対象が確率である場合、相互作用の強さを測る統計量は分類問題にも適用できます。

5.4.3 例

特徴量の相互作用がどんなものか実際に見てみましょう。自転車のレンタル数の予測について、天気とカレンダーの特徴量使ってSVMで予測したときの特徴量間の相互作用の強さを計算してみましょう。

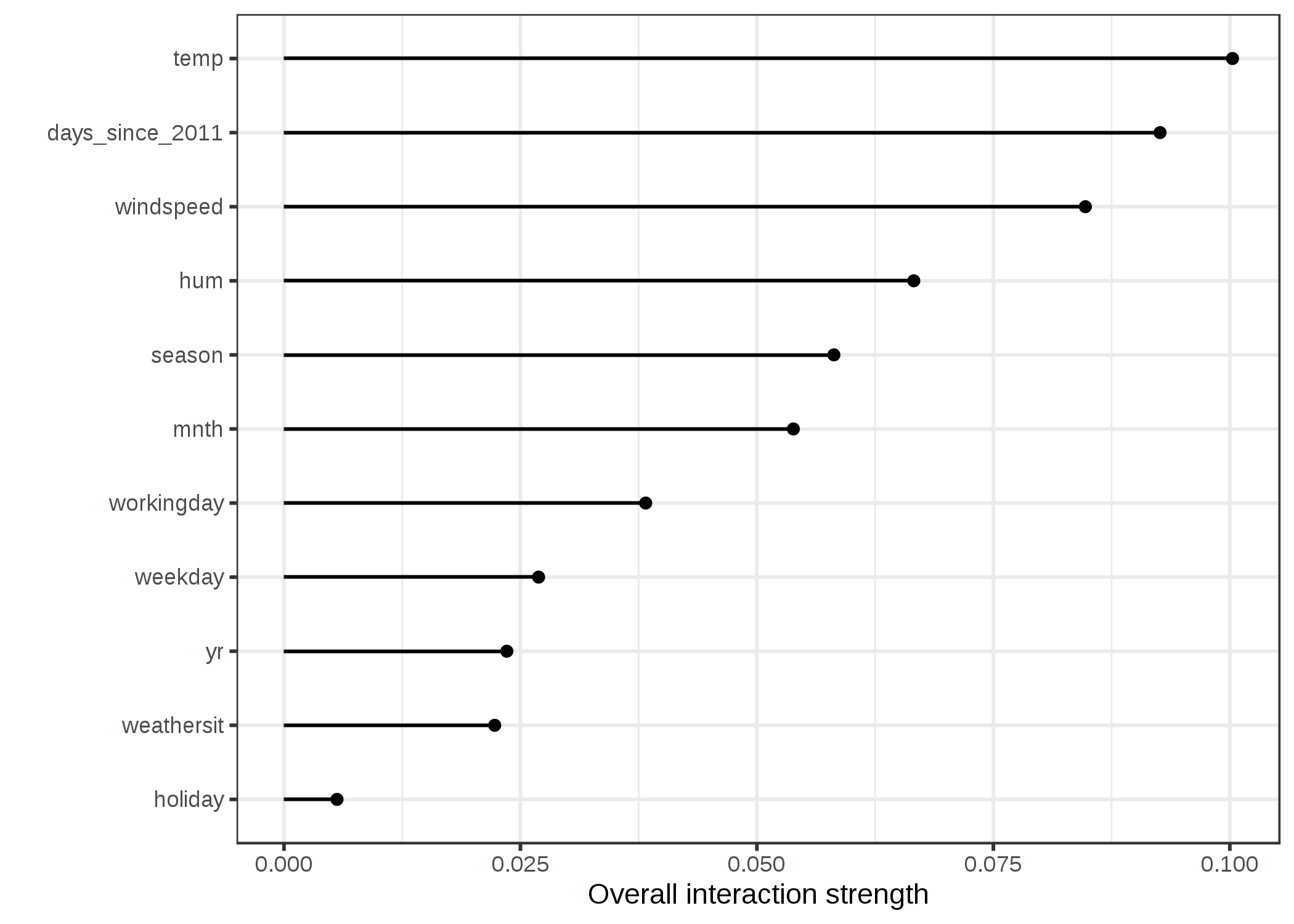
FIGURE 5.23: 自転車レンタル数をSVMで予測した時の、ある特徴量から他の特徴量に対する相互作用の強さ（H統計量）。全体的に、特徴量間の相互作用は非常に弱い（いずれも10%未満）。

次は分類問題に対する相互作用を計算してみましょう。様々なリスク要因が与えられた時の子宮頸がんの予測を学習したランダムフォレストの特徴量間の相互作用を分析してみましょう。

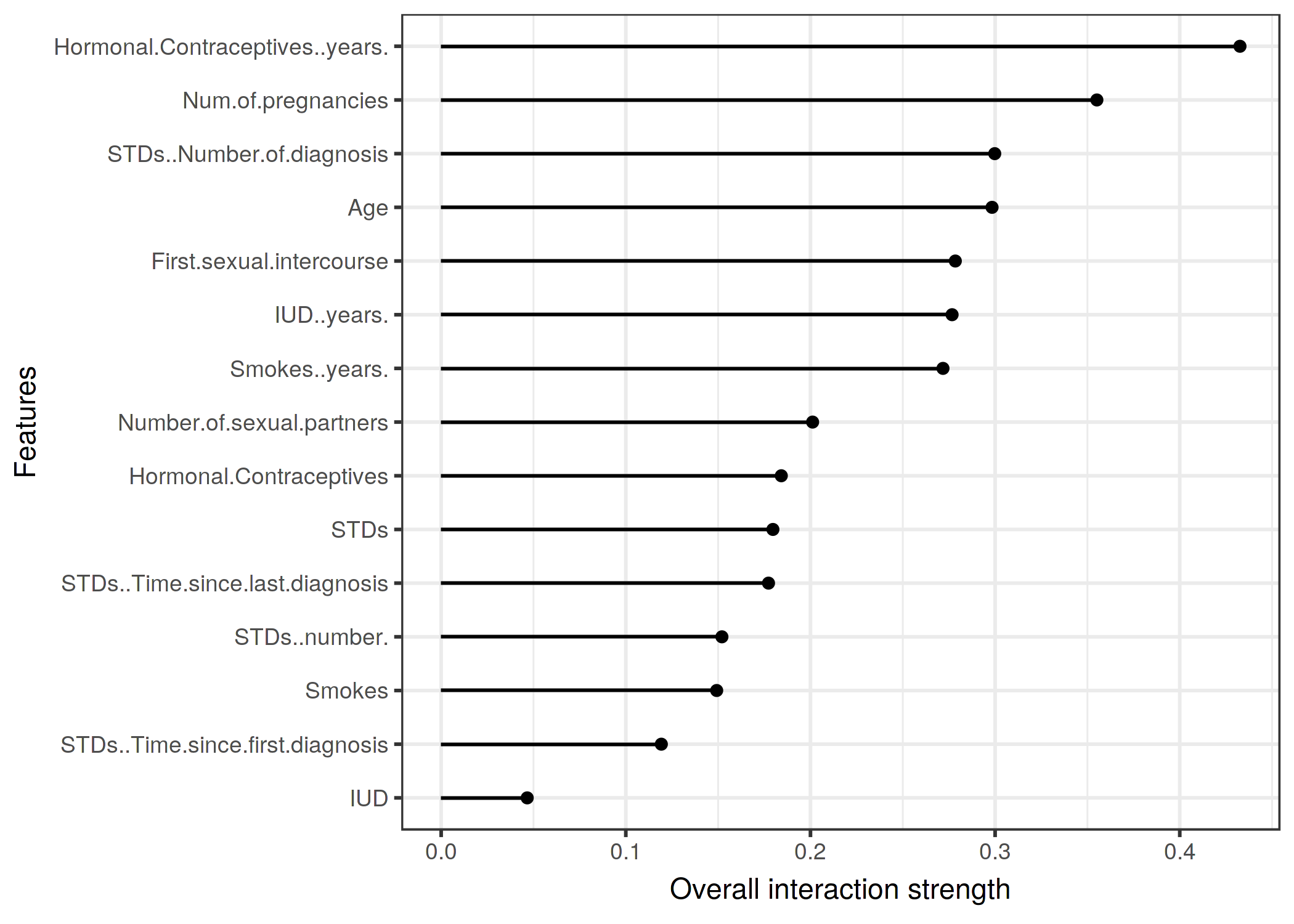
FIGURE 5.24: 子宮頸がんになる確率をランダムフォレストを用いて予測した時の、各特徴量から他の特徴量に対する相互作用の強さ（H統計量）。相互作用の強さは経口避妊薬の服用年数が1番高く、出産人数が次に高い。

それぞれの特徴量が他の特徴量との相互作用を確認しました。今度は特定の特徴量に注目して、その変数が他の各々の特徴量とどれだけ相互作用するかの、双方向的な相互作用に掘り下げていきましょう。

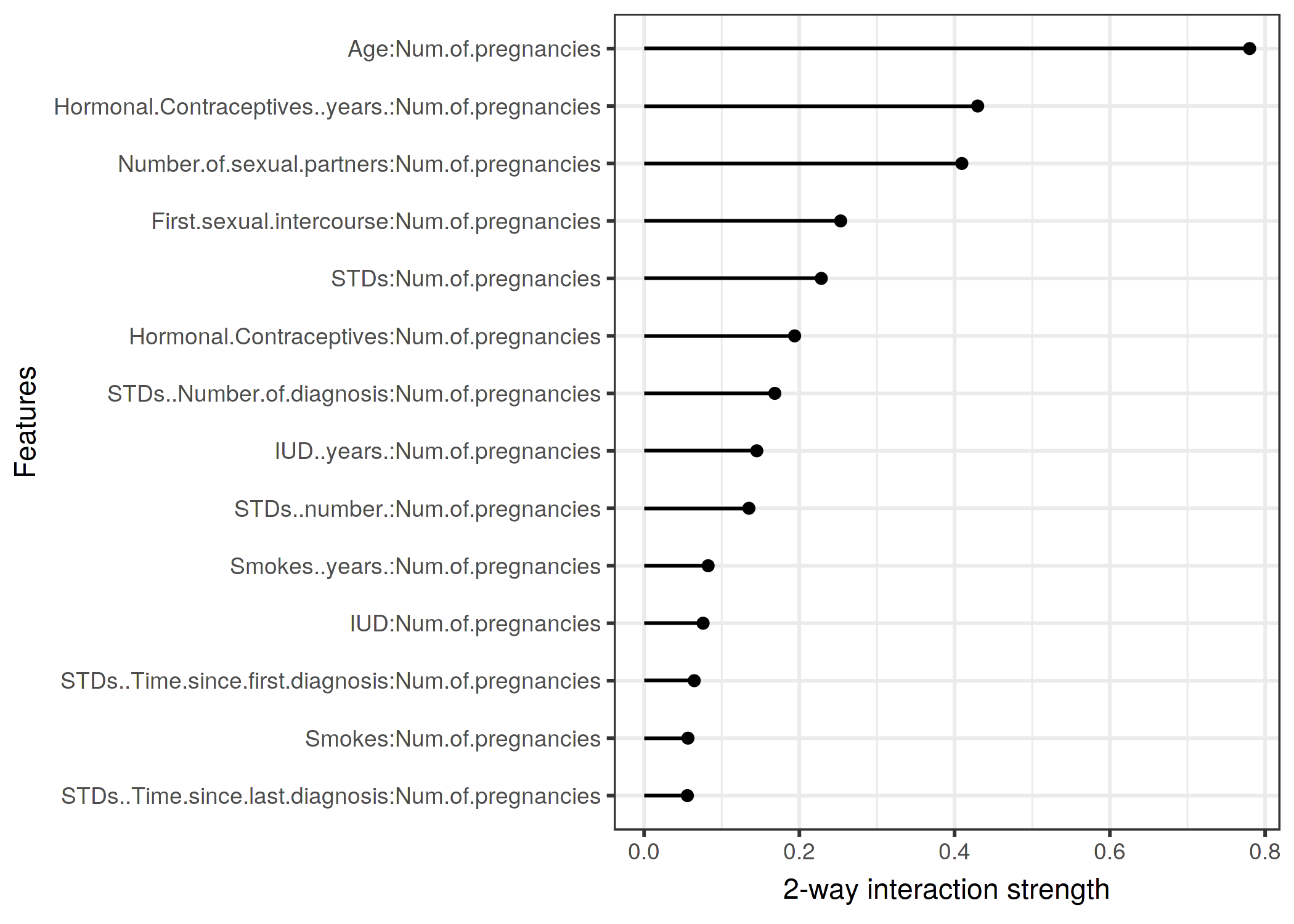
FIGURE 5.25: 妊娠回数と他の特徴量における双方向的な相互作用の強さ（H統計量）。妊娠回数と年齢に強い相互作用が認められる。

5.4.4 利点

相互作用の強さを計算するH統計量には、partial dependence decompositionという理論的な背景があります。

H 統計量は意味のある解釈を持ちます。この相互作用は、相互作用による分散の説明度合いとして定義されます。 H 統計量は無次元なので、特徴量間やモデル間で比較が可能です。

H 統計量は、特定の形式によらず、どのような種類の相互作用でも検出できます。 H 統計量を使うと、3つ以上の特徴量間における相互作用などの、より高次の相互作用も分析できます。

5.4.5 欠点

まず始めに、H特徴量は計算コストが高いため、計算に時間がかかります。

計算には周辺分布の計算が必要です。この計算は、もし全てのデータ点を使用しないのであれば、推定がばらつきます。これは、データをサンプリングすると、推定値は実行ごとに異なり結果が不安定になるということです。安定した結果を得るために、もしデータが十分であれば、数回 H 統計量の計算を繰り返すことをおすすめします。

また、相互作用が 0 より有意に大きいかどうかは不明瞭です。これには、仮説検定が必要かもしれませんが、このモデル非依存な検定は存在しません。

検定に関して言えば、相互作用が「強い」と考えるに足るH統計量の大きさを決めることも難しいです。また、H 統計量は 1 より大きくなる場合もあり、この場合解釈が難しくなります。

H 統計量は相互作用の大きさを表しますが、相互作用の性質を説明できません。そこで partial dependence plots が登場します。主な作業の流れとしては、まず相互作用の大きさを測ったのち、関心のある相互作用について2次元の partial dependence plots を作成します。

H 統計量は入力がピクセルの場合得られる効果が少なくなります。このため、この方法は画像の分類に対しては有効ではありません。

相互作用の統計は、特徴量を独立にシャッフルできるという仮定のもとに成り立ちます。もし特徴量間が強く相関する場合、この仮定は成り立たなくなるため、**実際には起こらないであろう特徴量の組み合わせをつくります。これは PDP についても同様です。ただし、これが過大評価に繋がるか過小評価に繋がるのかは一概に言えません。

小規模なシミュレーションでは、期待とは異なる奇妙な振舞いをします。しかし、これは観測データの不足による不確かさによるものです。

5.4.6 実装

本書で用いた R の iml パッケージは現行版をCRAN から、開発版は Github から入手できます。他にも特定のモデルを対象にした実装があります。 R パッケージの pre は RuleFit とH統計量を実装しています。 R パッケージの gbm は勾配ブースティングモデルと H 統計量を実装しています。

5.4.7 代替手法

H 統計量が相互作用を定量化する唯一の手法ではありません。

Hooker (2004)³² による Variable Interaction Networks (VIN) は、予測関数を主効果と相互作用に分解する方法です。特徴量間の相互作用はネットワークとして可視化されます。不運にも、まだVINのソフトウェアは存在しません。

Greenwell ら(2018)³³ によって、2つの特徴量の相互作用を定量化するための pertial dependence が提案されました。この方法は、ある特徴量の重要度（partial dependence functionの分散として定義される）について、他の特徴量の値を固定した上で測ります。もし分散が大きい場合特徴量は相互作用し、分散が 0 である場合相互作用はありません。この機能を提供する R パッケージ vip は Githubから利用できます。このパッケージでは partial dependence plots や feature importance などの機能も含みます。

Friedman, Jerome H, and Bogdan E Popescu. "Predictive learning via rule ensembles." The Annals of Applied Statistics. JSTOR, 916–54. (2008).↩
Hooker, Giles. "Discovering additive structure in black box functions." Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining. (2004).↩
Greenwell, Brandon M., Bradley C. Boehmke, and Andrew J. McCarthy. "A simple and effective model-based variable importance measure." arXiv preprint arXiv:1805.04755 (2018).↩