5.7 Local Surrogate (LIME)

ローカルサロゲートモデルは解釈可能なモデルであり、ブラックボックスな機械学習モデルの個々の予測を説明するために用いられます。 Local interpretable model-agnostic explanations (LIME)36という論文の中で、具体的に局所的なサロゲートモデルの実装が提案されました。 サロゲートモデルは根底にあるブラックボックスモデルの予測を近似するように学習されます。 グローバルなサロゲートモデルを学習する代わりに、LIME は個々の予測を説明するためにローカルサロゲートモデルを学習することに焦点を当てています。

アイデアはとても直感的です。 最初に、学習データのことは忘れて、データを入れると予測値を返すブラックボックスモデルを持っているだけの状態を想像してください。 何度でもボックスを調べることができます。 目的は機械学習モデルがなぜ特定の予測を返すか理解することです。 LIME は、機械学習モデルの入力データに変動を加えた時、予測にどのような変化が起こるかを検証します。 LIME は、サンプルの特徴量の値を置き換えて得られた新しいデータセットを作成し、ブラックボックスモデルで予測します。 そして、この新しいデータセットに基づいて、解釈可能なモデルを学習します。このモデルは、サンプルされたインスタンスと関心のあるインスタンスの近接性によって重み付けされます。 解釈可能なモデルには interpretable models の章に記載されている Lasso や decision tree などのどのモデルも使用できます。 学習されたモデルは局所的には機械学習モデルの予測を近似していますが、大域的にはよい近似にグローバルになるとは言えません。 この種の正確性は局所忠実性 (local fidelity) とも呼ばれます。

数学的には、解釈可能な制約を加えたローカルサロゲートモデルは次のように表現されます。

\[\text{explanation}(x)=\arg\min_{g\in{}G}L(f,g,\pi_x)+\Omega(g)\]

インスタンス x に対する説明モデルは、元のモデル f (例: xgboost モデル)の予測をどの程度説明できるかを表す損失 L (例: 二乗和誤差)を最小化するようなモデル g（例: 線形回帰モデル）となり、このモデルの複雑さ \(\Omega(g)\) は小さい (例: より少ない特徴量)必要があります。 G は可能な説明の族で、例えばすべての可能な線形回帰モデル、などです。 近似度 (proximity measure) \(\pi_x\) はインスタンス x を説明するために考慮する近傍をどの程度大きくするか定義します。 実際、LIME は損失関数を最適化しているだけです。 ユーザーは、線形回帰モデルが使用する特徴量の数の最大を選択することなどにより、複雑性を決定する必要があります。

ローカルサロゲートモデルは、次のように学習されます。

  • ブラックボックスな予測を説明したいインスタンスを選びます。
  • データセットを摂動させ、新たなデータ点に対するブラックボックスな予測を得ます。
  • 新しいサンプルを、関心のあるインスタンスへの近さに応じて重み付けします。
  • ばらつきを加えて作成したデータセットで重み付きの解釈可能なモデルを学習します。
  • 解釈可能な局所的なモデルによって予測を説明します。

例えば、現在の R と Python での実装では、線形回帰を解釈可能な代理モデルとして選択できます。 事前に、解釈可能なモデルが持つ特徴量の数 K を選択しなければなりません。 K が低ければ低いほど、モデルは解釈しやすくなります。 K が高ければ高いほど、より忠実なモデルとなります。 ちょうど K 個の特徴量を学習する方法はいくつかあります。 Lasso は良い選択と言えます。 正則化パラメータ \(\lambda\) が大きい Lasso は何の特徴量もないモデルとなります。 ゆっくりと \(\lambda\) を減少させていきながら Lasso を再学習していくと、非ゼロの重みをもつ特徴量が現れます。 モデルが K 個の特徴量を持つならば、希望する特徴量の数にたどり着いたことになります。 他の戦略は、特徴量の前方選択または後方選択です。 これは、完全なモデル（= すべての特徴量を含む）もしくは切片のみのモデルから始めて、どの特徴量が追加または削除されたときに最も改善がみられるかを、モデルの特徴量が K 個になるまで繰り返しテストします。

どうやってデータにばらつきを持たせるのでしょうか。 これは、データのタイプ（テキスト、画像、表形式など）に依存します。 テキストや画像では、1つの単語もしくはスーパーピクセルのオン・オフを切り替えるという方法があります。 表形式のデータでは、LIMEはそれぞれの特徴量をその平均と標準偏差を持つ正規分布に基づいて摂動させることによって新たなサンプルを作り出します。

5.7.1 表形式データにおける LIME

表形式のデータは、各行がインスタンスを表し、各列が特徴量を表しています。 LIMEのサンプルは、対象のインスタンスの周辺から取得されるのではなく、学習データの重心から取得され、これが問題になります。 しかし、これにより、サンプル点のいくつかが興味の対象のデータ点と異なる予測値を持つ可能性が高くなります。そのため、LIME が少なくとも何らかの説明を学習できる可能性も高くなります。

どのように、サンプリングや局所的なモデルの学習をしているかは視覚的に説明するのがベストです。

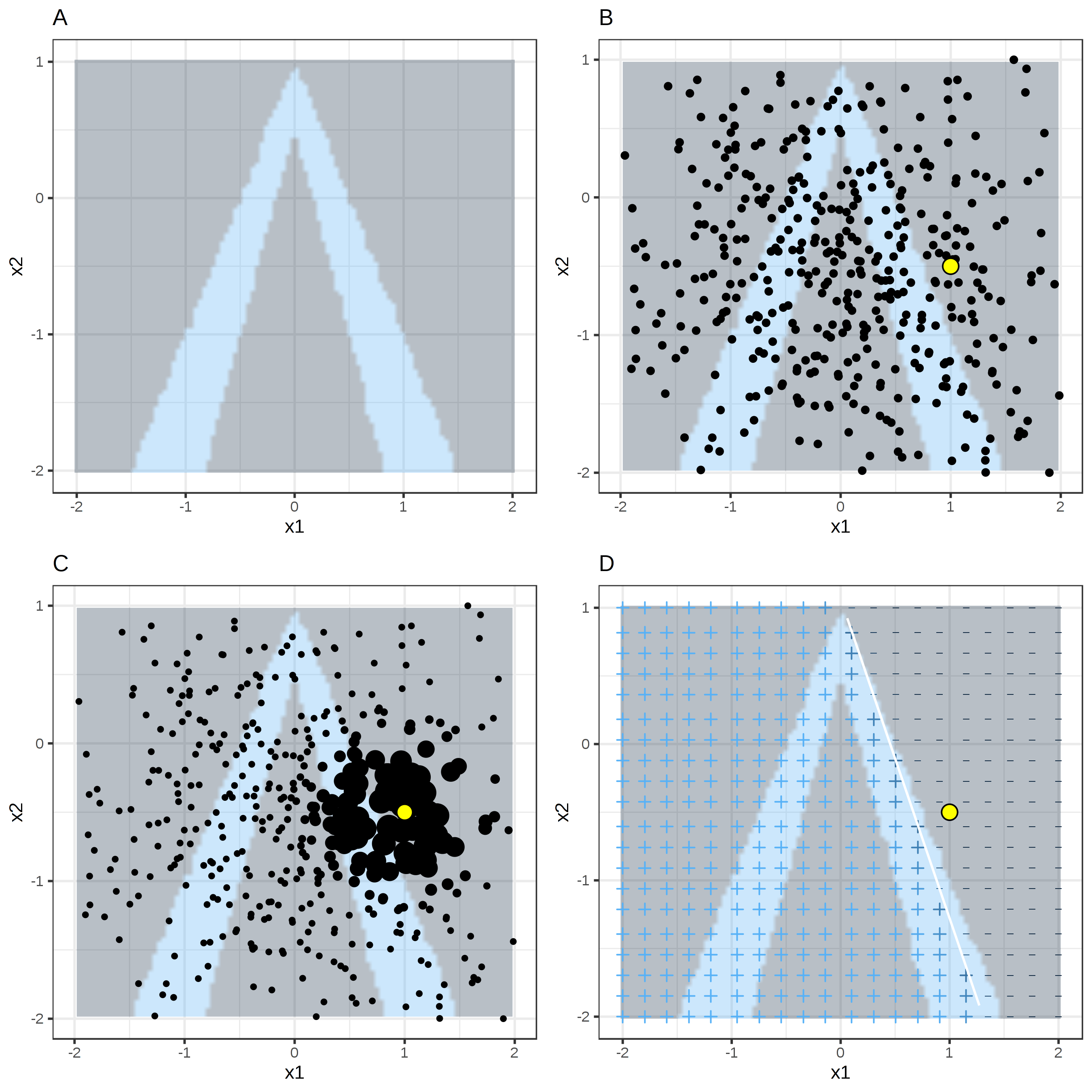
表形式データのLIMEアルゴリズム。 A) 特徴量 x1, x2 が与えられたときのランダムフォレストの予測。予測されたクラス: 1（暗い領域）または 0（明るい領域）。 B) 対象のインスタンス（大きい点）および正規分布から選ばれたデータ（小さい点）。 C) 対象のインスタンスの周辺に、より大きい重みを割り当てる。 D) グリッドの記号は重みづけされたサンプルから局所的に学習されたモデルの分類を示している。白い線は決定境界 (P(class=1) = 0.5) を示している。

FIGURE 5.32: 表形式データのLIMEアルゴリズム。 A) 特徴量 x1, x2 が与えられたときのランダムフォレストの予測。予測されたクラス: 1（暗い領域）または 0（明るい領域）。 B) 対象のインスタンス（大きい点）および正規分布から選ばれたデータ（小さい点）。 C) 対象のインスタンスの周辺に、より大きい重みを割り当てる。 D) グリッドの記号は重みづけされたサンプルから局所的に学習されたモデルの分類を示している。白い線は決定境界 (P(class=1) = 0.5) を示している。

いつものように、悪魔は細部に潜んでいます。 データ点の周りに意味のある近傍を定義することは難しいです。 LIMEは現在、近傍を定義するのに指数平滑化カーネル (exponential smoothing kernal) を使用しています。 平滑化カーネルは、2つのデータのインスタンスを受け取り、近接度を返す関数です。 カーネルの幅は近傍の大きさを定義します。 カーネル幅が小さいということは、ローカルモデルに影響を与えるにはインスタンスが非常に近くなければならないことを意味し、カーネル幅が大きいということは、遠くにあるインスタンスもモデルに影響を与えることを意味します。 LIME の Python 実装 (file lime/lime_tabular.py) を見ると、（正規化されたデータ上で）指数平滑化カーネルが用いられていることがわかります。 また、カーネル幅は、学習データの列の数の平方根の 0.75 倍になっていることもわかります。 一見、罪のないコードに見えますが、見て見ぬ振りをしている点があります。 重大な問題は、カーネルやその幅を決める良い方法が無いことです。 一体どこから 0.75 という数字がきているのでしょうか。 以下の図のように、カーネル幅を変えることによって説明を簡単にねじ曲げることができます。

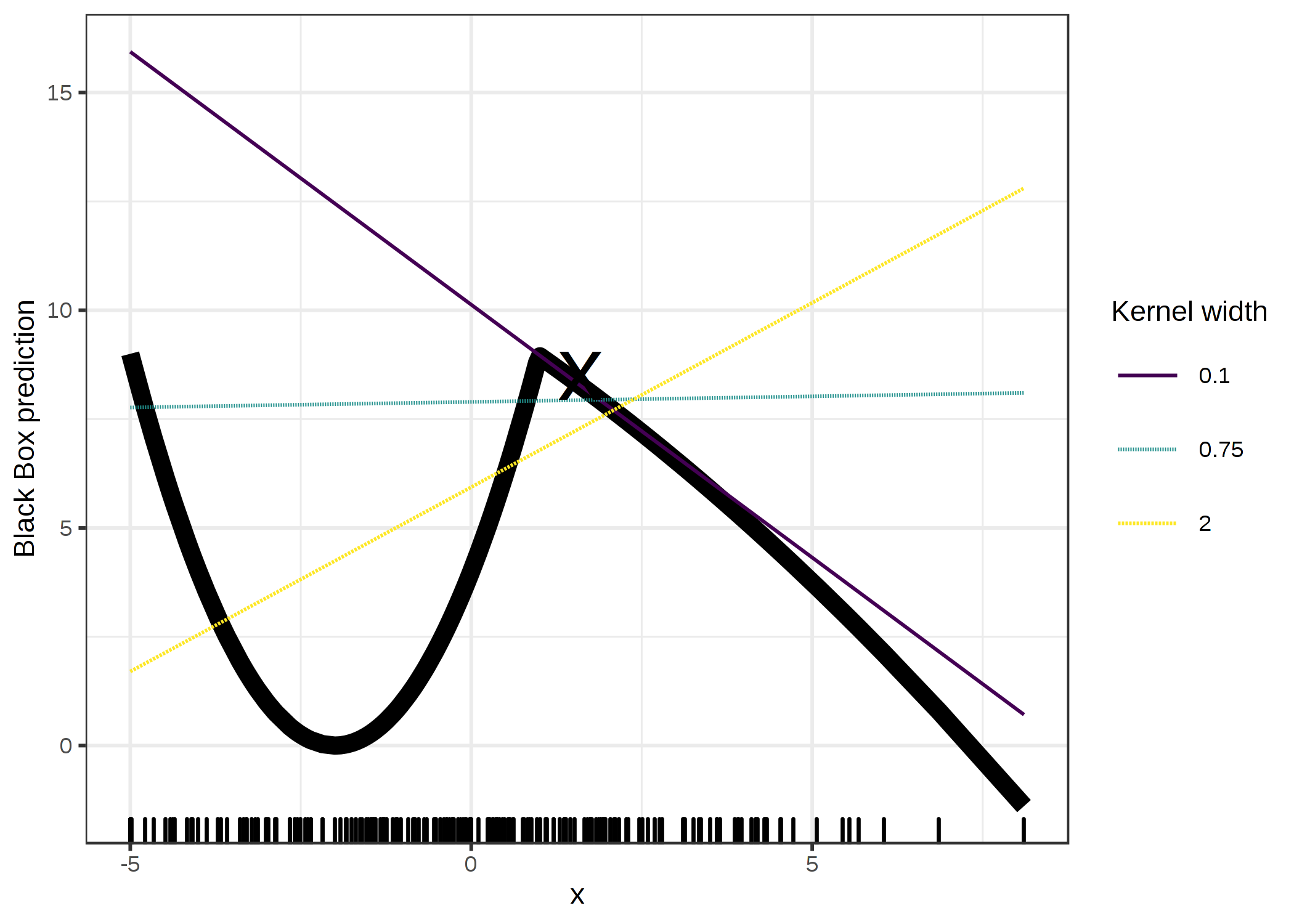
x = 1.6 という予測に対しての説明。1つの特徴量に依存しているブラックボックスモデルの予測値は太線で示し、データの分布は底部の棒線で示されている。異なるカーネル幅の3つのローカルサロゲートモデルが計算。線形回帰モデルの結果をみると、特徴量は x = 1.6 に対して負の効果があるか、正の効果があるか、あるいは全く効果がないかは、カーネル幅に依存していることがわかる。

FIGURE 5.33: x = 1.6 という予測に対しての説明。1つの特徴量に依存しているブラックボックスモデルの予測値は太線で示し、データの分布は底部の棒線で示されている。異なるカーネル幅の3つのローカルサロゲートモデルが計算。線形回帰モデルの結果をみると、特徴量は x = 1.6 に対して負の効果があるか、正の効果があるか、あるいは全く効果がないかは、カーネル幅に依存していることがわかる。

例では1つの特徴量しか取り上げませんでした。 より高次元な特徴量空間ではもっと悪くなります。 また、全ての特徴量を同じ距離尺度で扱っていいものかは非常に不明確です。 特徴量 x1 と特徴量 x2 で 1 だけ変化したとき、同じ距離だけ変化したと扱っていいのでしょうか。 距離尺度は極めて恣意的で、異なるの次元（別の特徴量）とは全く互換性がないかもしれません。

5.7.1.1 例

具体例を見てみましょう。 レンタル自転車のデータに戻って、予測問題をクラス分類の問題にします。 時間が経つにつれてレンタル自転車の人気が高まっているという傾向を考慮した上で、ある日のレンタサイクルの台数がトレンドラインより多いのか、少ないのかを知りたいとします。 「多い」とは平均のレンタル数を上回っているかどうかと解釈できますが、しかし、トレンドに対して調整されています。

まず、分類タスクに対して 100 個の決定木を用いたランダムフォレストを学習します。 天気やカレンダーの情報を元に、何日にレンタル自転車が平均 (trend-free) を上回るでしょうか。

説明は 2 個の特徴量から作成されます。 学習されたスパース局所線形モデルによって予測クラスの異なる2つのインスタンスを説明すると、次のようになります。

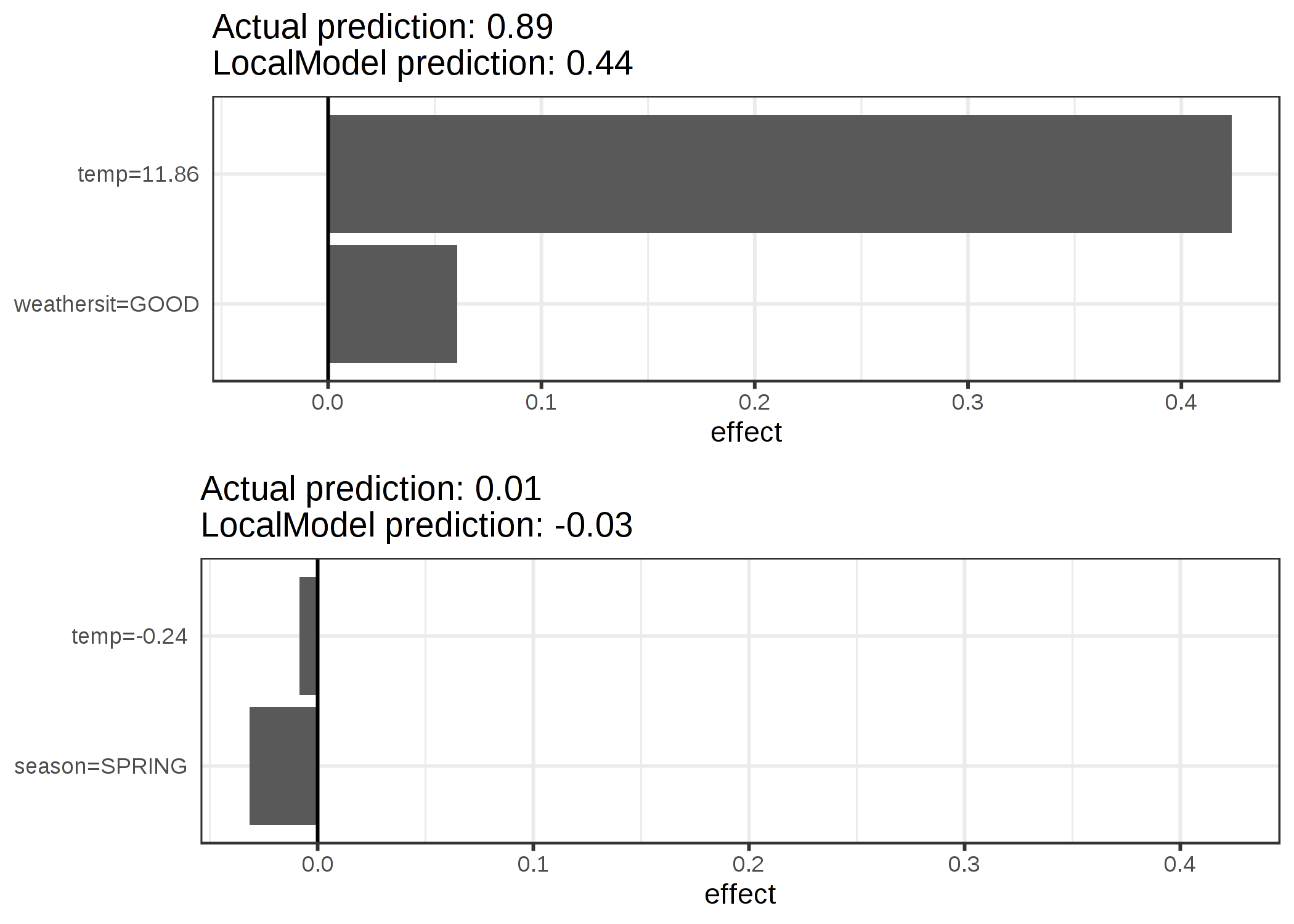
レンタル自転車データセットの2つのインスタンスに対する LIME の説明。暖かく天気が良いと予測に正の影響を与える。x 軸は特徴量の効果を示しており、実際の特徴量の値と重みの積に相当する。

FIGURE 5.34: レンタル自転車データセットの2つのインスタンスに対する LIME の説明。暖かく天気が良いと予測に正の影響を与える。x 軸は特徴量の効果を示しており、実際の特徴量の値と重みの積に相当する。

図から、量的特徴量よりもカテゴリカル特徴量の方が解釈しやすいことがわかりました。 1つの解決策は量的特徴量を度数によってカテゴライズすることです。

5.7.2 テキストデータに対するLIME

テキストデータに対する LIME は表形式データに対する LIME とは異なります。 データのバリエーションは異なる方法で生成されます。 元のテキストから始めて、新たなテキストは元のテキストからランダムに単語を削除することによって作成されます。 データセットは各単語に対するバイナリ特徴量で表現されます。 対応する単語が含まれている場合は 1、削除されている場合は 0 です。

5.7.2.1 例

この例では、YouTubeのコメント をスパムか通常のコメントかで分類します。

ブラックボックスモデルとして、文書の単語行列上で学習した深い決定木を使用します。 この行列では、各コメントは1つの文書（= 1行）であり、各列は特定の単語の出現回数を表します。 短い決定木は容易に理解できますが、今回は非常に深い木を扱います。 この決定木の代わりに、単語の埋め込み（抽象的なベクトル）に対して学習された再帰ニューラルネットワークや SVM を用いることもできます。 このデータセットから2つのコメントと対応するクラス (スパムなら1、通常のコメントなら0) を見てみましょう。

CONTENT CLASS
267 PSY is a good guy 0
173 For Christmas Song visit my channel! ;) 1

次のステップでは、局所モデルで使用される、データセットのバリエーションを作成します。 例えば、1つのコメントに対するバリエーションは次のようになります。

For Christmas Song visit my channel! ;) prob weight
2 1 0 1 1 0 0 1 0.17 0.57
3 0 1 1 1 1 0 1 0.17 0.71
4 1 0 0 1 1 1 1 0.99 0.71
5 1 0 1 1 1 1 1 0.99 0.86
6 0 1 1 1 0 0 1 0.17 0.57

各列は文中の1つの単語に対応します。 各行が1つのバリエーションを表しており、1 は単語がこのバリエーションの一部であることを意味し、0 はその単語が削除されたことを意味します。 バリエーションの1つに対応する文は、"Christmas Song visit my ;)"です。 "prob" の列は各バリエーションがスパムである予測確率を表します。 "weight"の列は元の文へのバリエーションの近接度を表しており、1 から削除された単語の割合を引いたものとして計算されます。 例えば、7語のうち1語が削除された場合、近接度は 1 - 1/7 = 0.86 となります。

2つの文（一方はスパム、もう一方はスパムでない）とLIMEのアルゴリズムによって推定された重みを見てみましょう。

case label_prob feature feature_weight
1 0.1701170 is 0.000000
1 0.1701170 good 0.000000
1 0.1701170 a 0.000000
2 0.9939024 channel! 6.180747
2 0.9939024 Christmas 0.000000
2 0.9939024 Song 0.000000

"チャンネル" という単語がスパムである確率が高いことを示しています。 スパムでないコメントの場合、どの単語が削除されてもクラス予測に影響がないため、ゼロ以外の重みは推定されませんでした。

5.7.3 画像データに対するLIME

このセクションは Verena Haunschmid が執筆しました。

画像に対する LIME は表形式データやテキストデータに対する LIME とは動作が異なります。 直感的には、複数のピクセルが1つのクラスに寄与するため、ひとつひとつのピクセルを摂動させることは意味がありません。 なので、ひとつひとつのピクセルをランダムに変更しても、予測結果はあまり変わらないでしょう。 そこで、画像を「スーパーピクセル」にセグメント化し、スーパーピクセルをオフ・オンに切り替えることで画像のバリエーションを作ります。 スーパーピクセルとは類似した色を相互接続したピクセルであり、それぞれのピクセルをグレーなどのユーザ定義の色に置き換えることでオフにできます。 また、ユーザは、それぞれの置換においてスーパーピクセルをオフにする確率を指定できます。

5.7.3.1 例

この例では、Inception V3 ニューラルネットワークによるクラス分類を見ていきます。 使用したのは、ボウルに入ったパンの画像です。 画像ごとに複数の予測ラベルを持つことができるので（確率でソートされている）、上位のラベルを説明できます。 1番目の予測は確率 77% で「ベーグル」であり、次に 4% で「ストロベリー」が続きます。 下の画像は、「ベーグル」と「ストロベリー」の LIME の説明を示しています。 説明はサンプル画像上に直接表示できます。 緑は画像のこの部分がラベルの確率を増加させることを意味し、赤は減少させることを意味します。

左：ボウルに入ったのパンの画像。中央と右: Google の Inception V3 ニューラルネットワークによる画像分類の上位2クラス（ベーグル、ストロベリー）に対する LIME の説明。

FIGURE 5.35: 左：ボウルに入ったのパンの画像。中央と右: Google の Inception V3 ニューラルネットワークによる画像分類の上位2クラス（ベーグル、ストロベリー）に対する LIME の説明。

「ベーグル」の予測と説明は、たとえ予測が間違っていたとしても、非常に合理的です。 実際には、中央に穴がないため、この画像はベーグルではありません。

5.7.4 長所

元の機械学習モデルを置き換えたとしても、説明にはそのまま同じ局所的な解釈可能モデルを使うことができます。 説明を受ける人は決定木を十分に理解していると仮定します。 ローカルサロゲートモデルを使用するため、実際の予測では決定木を使用していなくても、決定木を説明として使用できます。 例えば、予測モデルとして SVM を使用できます。 そして、xgboost モデルの方がうまく機能することがわかった場合は、SVM を xgboost モデルに置き換え、予測を説明する決定木はそのまま使用できます。

ローカルサロゲートモデルは、解釈可能なモデルの学習や解釈の文献や経験から恩恵を受けています。

Lasso や短い木を使用する場合、結果として得られる説明は短く（= 選択的）、対照的なものになる可能性があります。 したがって、人間に優しい説明になります。 これが、説明を受ける側が専門家でなかったり時間のない人であるようなアプリケーションで LIME がよく用いられる理由です。 ただし、完全な帰属に対しては十分ではないので、完全な予測の説明が法的に求められる場合などでは LIME が使われることはありません。 また、機械学習モデルのデバッグをする際、少しの理由ではなく全ての理由があると便利です。

LIME は表形式データ、テキストデータ、画像データ全てで有効な数少ない手法の1つです。

忠実度（解釈可能なモデルがブラックボックスの予測をどの程度近似しているか）は、対象の入力データ近傍におけるブラックボックスの予測を説明する際に、解釈可能なモデルがどれほど信頼できるかについて良いアイデアを与えてくれます。

LIME は Python (lime ライブラリ) や R (lime package と iml package) で実装されており、非常に簡単に使用できます。

局所代理モデルで作成された説明は、元のモデルが学習に使用したもの以外の特徴量を使用できます。 もちろん、これらの解釈可能な特徴量は入力データから得られるものでなければなりません。 テキスト分類器は特徴量として抽象的な単語の埋め込みを使用できますが、その説明は文内の単語の有無に基づいて行なうことができます。 回帰モデルが特徴量への解釈不可能な変換を用いて学習されたとしても、その説明は元の特徴量を使用して作成できます。 例えば、回帰モデルがアンケート回答の主成分分析 (PCA) の結果から学習されたとしても、LIME では元のアンケートの質問に対して学習できます。 LIME に解釈可能な特徴量を使用することは、特にモデルが解釈不可能な特徴量で学習されている場合に、他の手法に比べて大きな利点があります。

5.7.5 短所

表形式のデータに対して LIME を使用する際、近傍の正しい定義を与えることが非常に大きな未解決の問題となっています。 私はこれが LIME の最大の問題点であると考えており、LIME を慎重に使用することを推奨しています。 アプリケーションごとに異なるカーネルの設定を試して、説明が意味をなしているかを自分で確認する必要があります。 残念ながら、これが適切なカーネル幅を見つけるために私ができる最大限のアドバイスです。

サンプリングは LIME の現在の実装から改善される可能性があります。 データ点は、特徴量間の相関を無視して、ガウス分布からサンプリングされます。 これにより、実際には発生しがたいデータ点が局所的な説明モデルを学習する際に使用される可能性があります。

説明モデルの複雑さをあらかじめ定義する必要があります。 これに関しては、些細な不満です。 なぜなら、最終的には常にユーザが忠実度とスパース性の間の妥協点を定義する必要があるからです。

もう1つの非常に大きな問題点は、説明の不安定さです。 記事 37 の中で、著者はあるシミュレーションにおいて非常に近い2点の説明が大きく異なることを示しました。 また、私の経験上でも、サンプリングプロセスを繰り返すと得られる説明が異なってしまう場合があります。 不安定さは説明が信頼しがたいものであることを意味しており、これは致命的です。

結論として、具体的な実装として LIME を使用したローカルサロゲートモデルは非常に将来有望です。 しかし、この方法はまだ発展途上段階であり、安全に使用するには多くの問題を解決する必要があります。

  1. Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. "Why should I trust you?: Explaining the predictions of any classifier." Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. ACM (2016).↩

  2. Alvarez-Melis, David, and Tommi S. Jaakkola. "On the robustness of interpretability methods." arXiv preprint arXiv:1806.08049 (2018).↩