4.2 ロジスティック回帰
ロジスティック回帰は2つの可能な結果を伴う分類問題の確率をモデル化します。これは線形回帰モデルの分類問題への拡張です。
4.2.1 線形回帰モデルを分類のために使うと何がいけないか。
線形回帰モデルは回帰問題ではうまく働きますが、分類問題ではうまくいきません。 なぜでしょうか? 2クラス分類の場合、あるクラスを 0、もう一方を 1 とラベル付けし、線形回帰モデルを使ったとしましょう。 技術的にはうまく働き、線形モデルは重みを計算します。 しかし、この方法にはいくらか問題があります。
線形モデルは確率を出力せず、クラスを数字として扱い、点との距離を最小化するような最適な超平面に (単一の特徴量に対しては線として) 適合させます。 それは、単に、点の間の補間をしているだけなので、確率として解釈できません。
また、線形モデルは外挿し、0 より小さかったり、1 より大きな値を出力します。 これは分類問題に対する、より良いアプローチがあるかもしれないというよい徴候です。
予測結果が確率ではなく、点の間の線形補間なので、クラスを分けるための、意味のある閾値というものは存在しません。 この問題に関するわかりやすい説明はStackoverflow に示されています。
線形モデルは多クラス分類には拡張できません。 次のクラスを 2 だったり、3 だったりとラベル付けするかもしれません。 クラスの順序に意味のないときもあるでしょうが、線形モデルにおいては特徴量と予測クラスに不自然な関係性を作ることが強制されます。 同じような値に偶然なったクラスが他のクラスと近くなかったとしても、正の重みをもつ特徴量の値が高ければ高いほど、予測されるクラスはより大きな数になりやすくなっていきます。
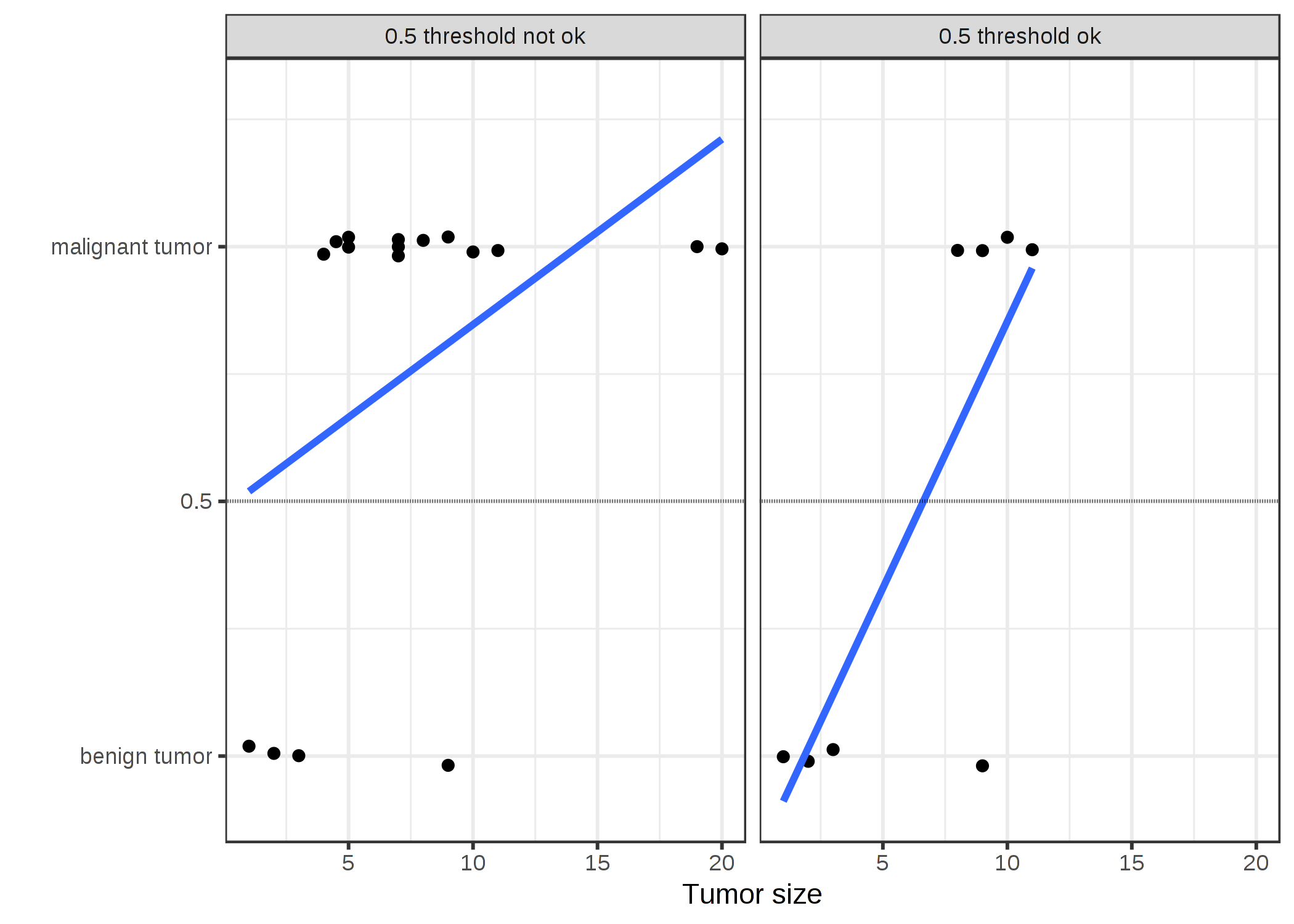
FIGURE 4.5: 線形モデルで大きさによって腫瘍が良性であるか、悪性であるか分類しています。直線は線形モデルの予測を表しています。左にあるデータでは 0.5 を閾値として用いています。いくつか悪性のケースが入った場合では、回帰直線はシフトし、0.5 はもはや閾値としては機能しなくなっています。表示する点を少しだけ減らして、見やすくしています。
4.2.2 理論
分類のための解決策は、ロジスティック回帰です。 直線や超平面を当てはめる代わりに、ロジスティック回帰モデルでは、ロジスティック関数を使用して、0 と 1 の間へ線形方程式の出力を変形します。 ロジスティック関数は次のように定義されます。
\[\text{logistic}(\eta)=\frac{1}{1+exp(-\eta)}\]
下図のようになります。
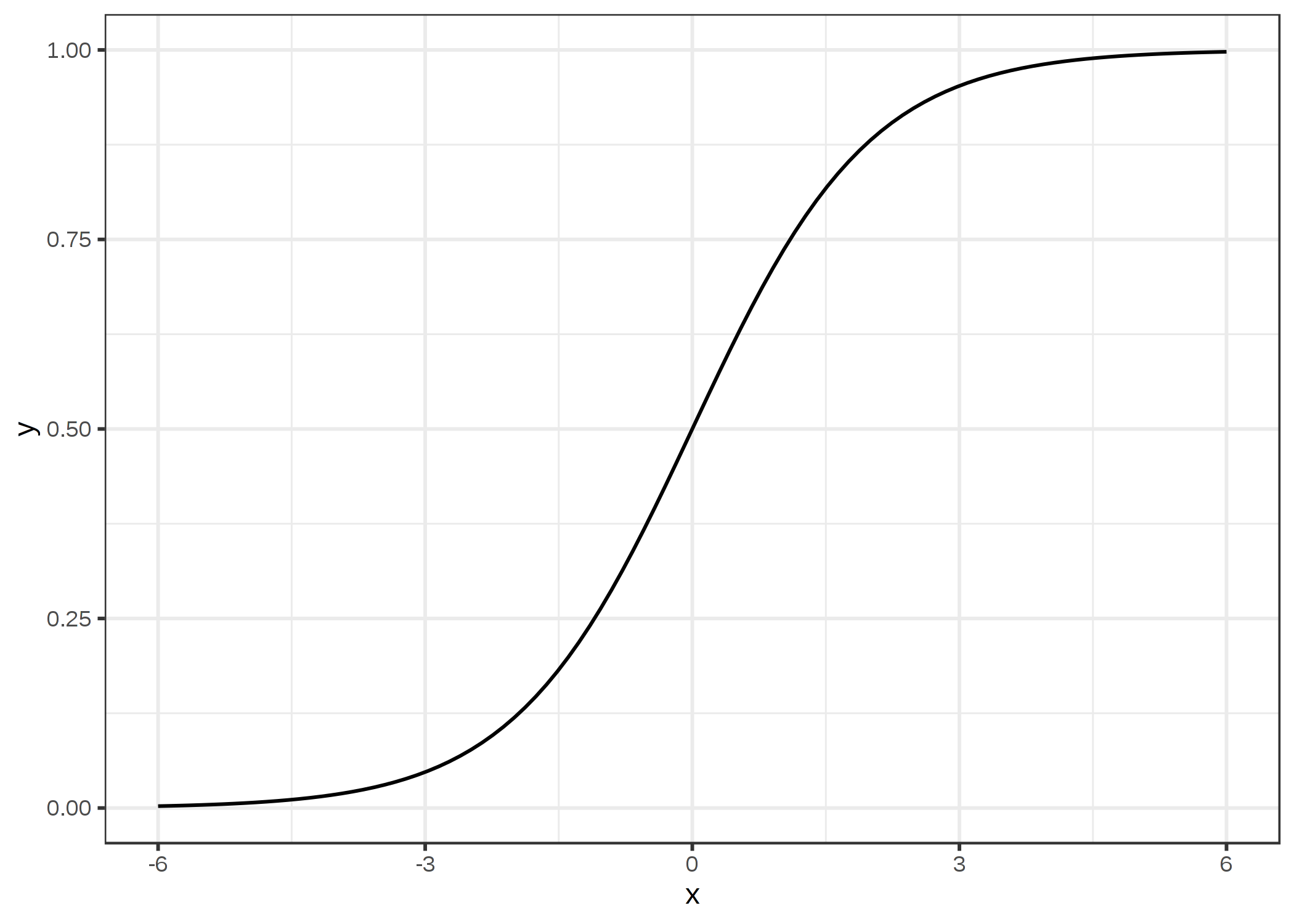
FIGURE 4.6: ロジスティック関数。 出力は 0 から 1 の間を取ります。 入力が 0 のとき、出力は 0.5 です。
線形回帰からロジスティック回帰への変換は理解しやすいです。 線形回帰モデルでは、結果と特徴量の関係を線形方程式でモデル化しています。
\[\hat{y}^{(i)}=\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}\]
分類において、値が 0 から 1 の間となるように、右式をロジスティック関数に組み込みます。 この変換によって、出力は 0 から 1 の間の値を取るようにできます。
\[P(y^{(i)}=1)=\frac{1}{1+exp(-(\beta_{0}+\beta_{1}x^{(i)}_{1}+\ldots+\beta_{p}x^{(i)}_{p}))}\]
腫瘍の大きさの例をもう一度見てみましょう。 線形回帰モデルの代わりにロジスティック回帰モデルを使っています。
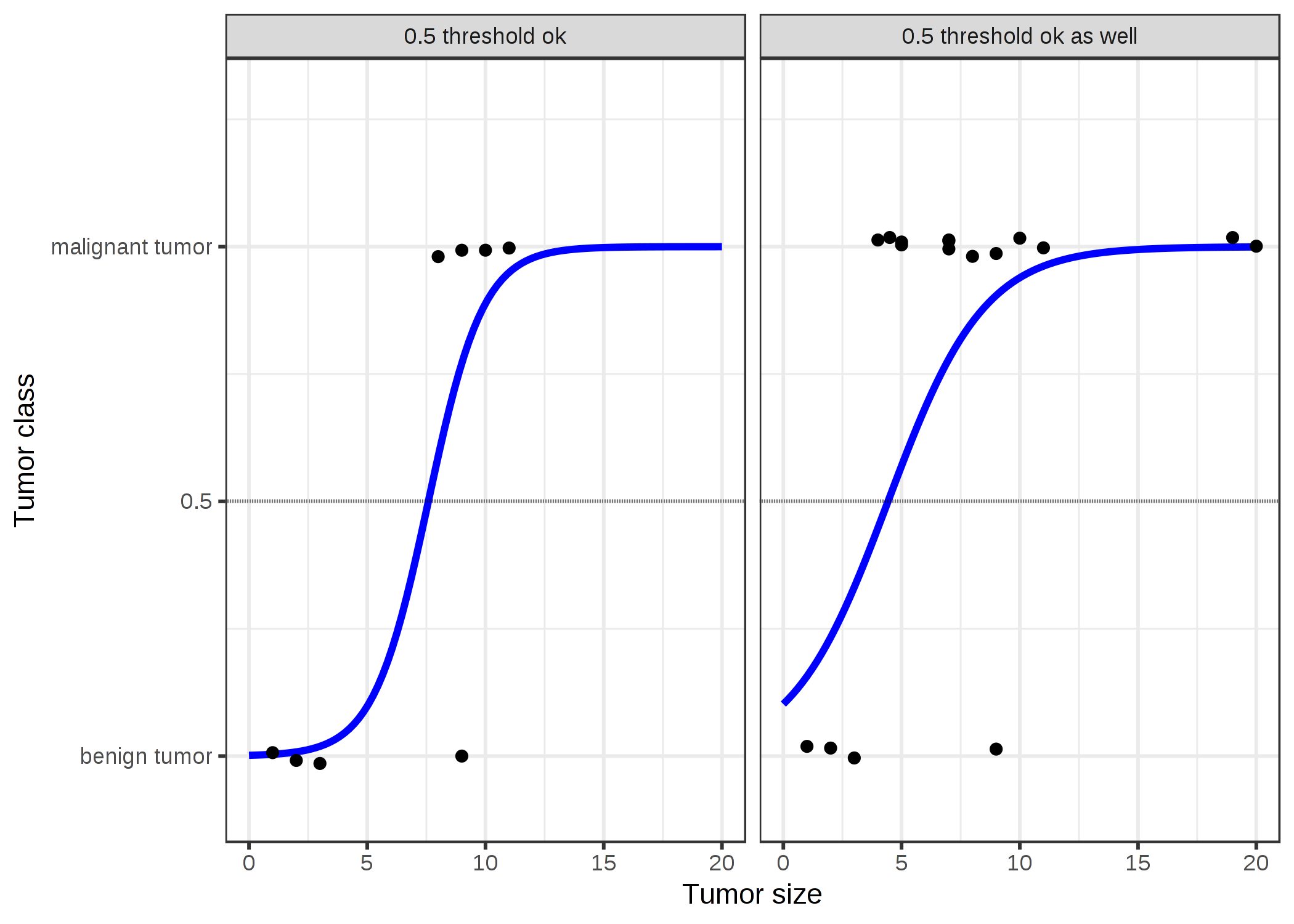
FIGURE 4.7: ロジスティック回帰モデルは、腫瘍のサイズに応じて、悪性と良性の間の正しい決定境界を見つけます。 この線は、データに適合するように変形されたロジスティック関数です。
ロジスティック回帰はうまく分類し、両方のケースで 0.5 を閾値として使うことができます。点を追加することは、推定された曲線にそこまで影響を与えません。
4.2.3 解釈性
ロジスティック回帰モデルの出力は 0 から 1 の確率で表現されるため、ロジスティック回帰の重みの解釈は線形回帰モデルの重みの解釈とは異なります。 重みは確率に対して、線形に影響を及ぼすわけではありません。 重みの合計はロジスティック関数によって確率に変換されます。 したがって、解釈のために、方程式の右側の線形項を式変形する必要があります。
\[log\left(\frac{P(y=1)}{1-P(y=1)}\right)=log\left(\frac{P(y=1)}{P(y=0)}\right)=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\]
この log()関数の中の項を "オッズ" (イベントの確率をイベントが起こらない確率で割ったもの) といい、対数をとったものを対数オッズといいます。
この式はロジスティック回帰モデルが対数オッズに対する線形モデルであることを表しています。 すばらしい! それでは役に立つようには見えません。 少し項を入れ替えると、特徴量 \(x_j\) の1つを 1 単位変化した時、どのように予測が変化するか分かります。 このように変換すると、exp() 関数を方程式の両辺にかけることができます。
\[\frac{P(y=1)}{1-P(y=1)}=odds=exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\right)\]
そして、1つの特徴量の値を 1 増加させると何が起きるかを比較します。 このとき、差をみるのではなく、2つの予測の比に注目します。
\[\frac{odds_{x_j+1}}{odds}=\frac{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}(x_{j}+1)+\ldots+\beta_{p}x_{p}\right)}{exp\left(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{j}x_{j}+\ldots+\beta_{p}x_{p}\right)}\]
以下のルールを適用します。
\[\frac{exp(a)}{exp(b)}=exp(a-b)\]
そして、項を削除します。
\[\frac{odds_{x_j+1}}{odds}=exp\left(\beta_{j}(x_{j}+1)-\beta_{j}x_{j}\right)=exp\left(\beta_j\right)\]
最終的に、特徴量の重みの exp() のような単純な式を得ることができます。 特徴量の中の 1 単位の変化は、オッズ比を \(\exp(\beta_j)\) 倍に変化させます。 この式は以下のように解釈できます。 \(x_j\) を 1 単位だけ変化させると、対応する重みの値だけ対数オッズ比が増加します。 ほとんどの人は、対数について頭で考えることが困難なため、オッズ比を解釈します。 オッズ比を解釈するには慣れが必要です。 例えば、もしオッズ比として 2 が与えられたら、 y=0 の確率より y=1 の方が 2 倍高いことを意味します。 重み(=対数オッズ比)が 0.7 の場合、それに対応する特徴量を 1 単位増やすと、オッズに exp(0.7)(=約 2)が乗算され、オッズは4に変わります。 しかし、通常はオッズを扱う必要がなく、重みだけをオッズ比として解釈します。 オッズを実際に計算するためには、それぞれの特徴量に値を設定する必要があるためです。 これは、データセットの特定のインスタンスに注目したいときのみ意味を成します。
特徴量の種類に応じて、ロジスティック回帰の解釈は異なります。
- 数的特徴量 (Numerical feature)の場合: \(x_{j}\) を 1 単位だけ増加させると、予測されるオッズは \(\exp(\beta_{j})\) 倍に変化します。
- バイナリ特徴量 (Binary categorical feature) の場合: 特徴量の2つの値のうちの1つは 参照カテゴリ (いくつかのプログラミング言語では、0 とエンコードされる) です。 特徴量 \(x_{j}\) が参照カテゴリから他のカテゴリに変化した時、オッズは \(\exp(\beta_{j})\) 倍になります。
- 2つ以上のカテゴリを持つ、カテゴリカルデータの場合: 複数のカテゴリを扱う1つの方法は one-hot-encoding です。one-hot-encoding はそれぞれのカテゴリがそれぞれ列を持ちます。 L 個のカテゴリを持つとき、L-1 列のみ必要で、そうでなければ、パラメータが過剰となります。 L 番目のカテゴリは参照カテゴリである必要があります。 他にも、線形回帰で使用可能な任意のエンコード方法を用いることができます。 それぞれのカテゴリの解釈はバイナリ特徴量の解釈と同様です。
- 切片\(\beta_{0}\): 全ての特徴量がゼロでカテゴリカル特徴量が参照カテゴリの時、予測されるオッズの値は \(\exp(\beta_{0})\) です。 切片の重みの解釈は、たいてい意味がありません。
4.2.4 例
ここでは、ロジスティック回帰をリスク要因に基づいた子宮頸がんの予測に使用します。 以下の表は推測された重み、オッズ比、予測の標準誤差を表しています。
| Weight | Odds ratio | Std. Error | |
|---|---|---|---|
| Intercept | -2.91 | 0.05 | 0.32 |
| Hormonal contraceptives y/n | -0.12 | 0.89 | 0.30 |
| Smokes y/n | 0.26 | 1.29 | 0.37 |
| Num. of pregnancies | 0.04 | 1.04 | 0.10 |
| Num. of diagnosed STDs | 0.82 | 2.26 | 0.33 |
| Intrauterine device y/n | 0.62 | 1.85 | 0.40 |
量的特徴量の解釈 ("Num. of diagnosed STDs"): STDs (性感染症, sexually transmitted diseases) と診断された回数が増えると、癌かそうでないかのオッズは 2.26 倍変化します。 ただし、他の特徴量を固定した場合です。 相関は因果関係を示しているとは限らないことに注意してください。
カテゴリカル特徴量の解釈("Hormonal contraceptives y/n"): ホルモン避妊薬を使っている女性に関して、癌かそうでないかのオッズは、ホルモン避妊薬を使っていない人に比べて 0.89 倍低いです。 ただし、他の特徴量を固定した場合です。
線形モデルと同様に、解釈では常に他の特徴量が固定されているという仮定の元で行われます。
4.2.5 長所と短所
線形回帰モデルの長所と短所は、ロジスティック回帰モデルにも当てはまります。
ロジスティック回帰は様々な分野の人々によって広く使用されていますが、その表現力の低さが問題であり(たとえば、相互作用を手動で追加する必要があります)、他のモデルの方が予測性能が優れていることもあります。
ロジスティック回帰モデルのもう1つの欠点は、重みの解釈は乗法的であり、加法的ではないため、解釈が難しくなることです。
ロジスティック回帰は、完全分離に悩まされることがあります。 2つのクラスを完全に分離できる特徴量がある場合、ロジスティック回帰モデルは学習できなくなります。 これは、その特徴量の最適な重みが無限大となり、収束しないためです。 このような特徴量はクラス分類の際に有用なので、これは残念なことです。 しかし、このように2つのクラスを分離する単純なルールがある場合は、機械学習は必要ありません。 完全分離の問題は、重みのペナルティを導入するか、重みの事前分布を定義することで解決できます。
良い面として、ロジスティック回帰モデルは分類モデルであるだけでなく、確率を出力します。 これは、最終的な分類結果しか提供できないモデルに比べて大きな利点と言えます。 インスタンスが、あるクラスに分類される確率が51%ではなく99%であること知れるのは大きな違いがあります。
ロジスティック回帰は、2クラス分類から多クラス分類に拡張できます。 それは多項回帰 (Multinomial Regression) と呼ばれます。
4.2.6 ソフトウェア
上記の例は、すべて R の glm 関数を使用しました。 ロジスティック回帰は、Python、Java、Stata、Matlab など、データ分析に用いられるあらゆるプログラミング言語で実装されています。