4.3 GLM、GAM、その他
線形モデルは、予測を特徴量の重み付き和としてモデル化する点が、最大の長所であり短所でもあります。 それに加えて、線形モデルは多くの仮定を必要とします。 悪いニュースは(実際にはニュースではありませんが)、それらの仮定が現実問題には当てはまらないということがしばしば起こるということです。 例えば、結果が正規分布に従わなかったり、特徴量間に相互作用があったり、あるいは、特徴量と結果の間の真の関係が非線形であったりするような場合です。 一方で良いニュースは、専門家のコミュニティが、この線形回帰モデルという単純なものを、スイスのアーミーナイフのように扱いやすくするために様々な改良をしてきたということです。
この章は、線形モデルを拡張するための明確なガイドを提供しようとするものではなく、一般化線形モデル(GLM)や一般化加法モデル(GAM)などの拡張モデルの概要を紹介し、直感的な理解を与えることが目的です。 したがって、この章を読み終わった後に、どのように線形モデルを拡張するのかについてしっかりと理解する必要があるでしょう。 もしあなたが最初に線形回帰モデルについて理解したいのにも関わらず、まだ線形回帰モデルの章を読んでいないのなら、先にその章を読むことをお勧めします。
線形回帰モデルの式を思い出してみましょう。
\[y=\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}+\epsilon\]
線形回帰モデルは、結果 y は、p 個の特徴量の重み付き和に正規分布に従う誤差 \(\epsilon\) が付与されたものであると仮定しています。 このようにデータを定式化することで、モデルの高い解釈可能性が得られるわけです。 線形回帰モデルでは、特徴量の効果は加法的で、相互作用はなく、特徴量と出力の関係は線形です。つまり、特徴量が 1 増加すると、直接的に予測結果が増加/減少します。 線形モデルを使用することで、特徴量と予測結果の関係を、1つの数値、すなわち推定された重みとして表現します。
しかし、単純な重み付き和は制約として強すぎるため、現実世界の多くの予測問題にそのまま適用することは出来ません。 この章では、線形回帰モデルの典型的な3つの問題を取り上げ、それらをどう解決するかについて紹介します。 モデル仮定に反する可能性のある問題は他にも多くありますが、次の図に示す3つの問題に焦点を当てます。
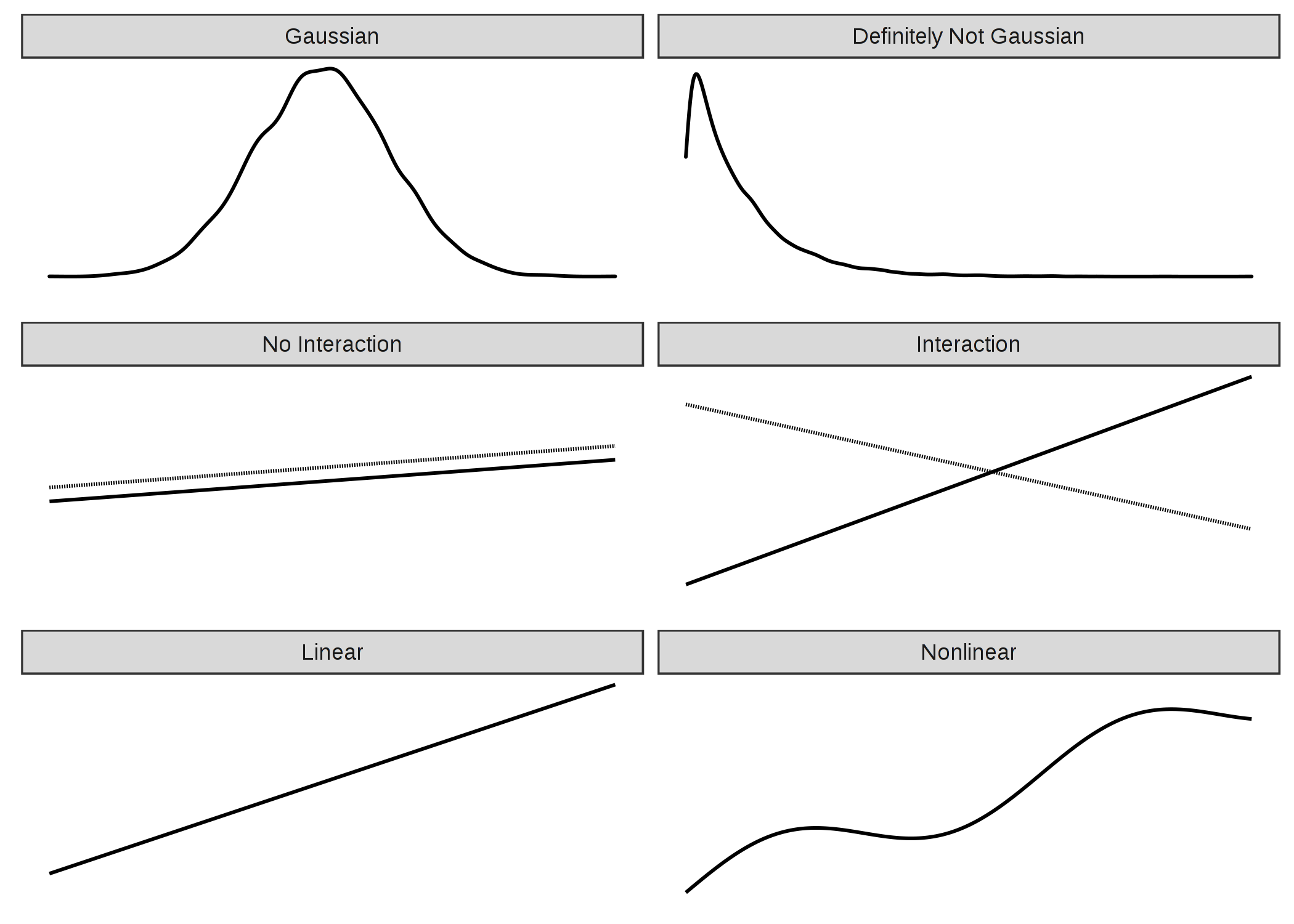
FIGURE 4.8: 線形モデルの3つの仮定(左側):特徴量に対する出力が正規分布であること、加法性が成り立つ(=相互作用がない)こと、及び線形関係にあること。現実では通常これらの仮定を満たさない(右側):出力が正規分布に従わなかったり、特徴量間に相互作用が存在したり、非線形の関係があったりするかもしれません。
これらすべての問題に対する解決策があります。
問題: 特徴量が与えられたときの結果 y が、正規分布に従わない。
例: ある日に何分間、自転車に乗るかを予測したいとします。
この場合、特徴量としては曜日や天気などがあります。 しかしながら、線形モデルを使用した場合、正規分布を想定しているため、0 分以下にならないとは限らず、負の時間を予測してしまうかもしれません。 その他の例として、線形モデルを使用して確率を予測した場合、負または1より大きい確率が予測値として得られることになります。
解決策: 一般化線形モデル(GLMs)
問題: 特徴量間に相互作用が存在する。
例: 私は、小雨が降るとサイクリングしたいという気持ちが少し萎えますが、夏のラッシュアワー時には雨を歓迎します。 それは、晴天を好むサイクリストが全員家にいて、自転車道が空くからです。 これは時間と天気の間の相互作用であるため、単純な加法モデルでは捉えることができません。
解決策: 相互作用項を手動で追加する
問題: 特徴量と結果 y の間の真の関係性が線形ではない。
例: 摂氏0度から25度の間では、自転車に乗りたいという私の欲求に対する温度の影響は、線形である可能性があります。 つまり、気温が0度から1度に上昇した場合と、20度から21度に上昇した場合のモチベーションの増加は同じということです。 しかし、その気温よりが高くなれば、暑すぎるときに自転車に乗るのは好きでないので、サイクリングへのモチベーションは横ばいになり、やがて低下します。
解決策: 一般化された加法モデル (GAM); 特徴量の変換
この章では、これら3つの問題の解決策を示します。 線形モデルの拡張は他にも多くありますが、ここでは割愛します。 ここで全てを説明しようとすれば、この章自体がすでに他の多くの専門書の中で説明されている内容を集めた本となってしまうでしょう。 とはいえ、せっかくですので、章の終わりで線形モデル拡張について問題と解決策のちょっとした概要を作成しておきました。 解決策の名前は、自身で詳細を調べるときに役に立つことでしょう。
4.3.1 結果が正規分布に従わない場合 - GLMs
線形回帰モデルは、特徴量が与えられたときの結果は正規分布に従うと仮定としています。 しかし、この仮定が成り立たない場合は多くあります。 結果は、カテゴリ (がん or 健康)、計数 (子供の数)、出来事が起こるまでの時間 (機械が故障するまでの時間)、少数のとても大きな数が存在する偏った出力 (世帯収入) などがあります。 実は、線形回帰モデルはこれらすべてのタイプに拡張できます。 この拡張は一般化線形モデル (Generalized Linear Models)もしくは省略してGLMsと呼ばれます。 この章では、GLMという用語を一般的なフレームワークとこのフレームワークに由来する特定のモデル、両方を表す際に使います。 GLM のコアとなる概念は、「特徴量の重み付き和を保持するが、結果の分布の非正規性を許容し、この分布の平均と重み付き和をある非線型関数で関連づけること」です。 例えば、ロジスティック回帰モデルでは結果が二項分布 (Bernoulli distribution) に従うことを仮定しており、ロジスティック関数を通して分布の平均と重み付き和が関連付けられています。
GLM は特徴量の重み付き和と、仮定された分布の平均を、リンク関数 g を用いて数学的に関連付けます。このとき、 g は結果の種類によって柔軟に決められます。
\[g(E_Y(y|x))=\beta_0+\beta_1{}x_{1}+\ldots{}\beta_p{}x_{p}\]
GLM は次の3つの要素からなります。 それは、リンク関数 g、重み付き和 \(X^T\beta\) (線形予測器とも呼ばれる) と、\(E_Y\) を定義する指数型分布族に由来する確率分布です。
指数型分布族は、分布の平均、分散、その他のパラメータを持つ指数が含まれた共通の式によって記述できる分布の集合です。 それ自体、とてつもなく広い分野であり、深入りはしたくないので、数学的な詳細まで今回は扱いません。 Wikipedia にはよく整理された指数型分布族に該当する分布の表があります。 このリストの中ならどの分布でも GLM に適用できます。 予測したい結果の種類に応じて、適切な分布を選んでください。 例えば、結果が数 (例:一家庭における子供の数) ならばポアソン分布、 結果が常に正 (例:2つのイベント間の時間) ならば指数分布が良いでしょう。
GLM の特殊な場合として、古典的な線形モデルについて考えてみましょう。 線形モデルにおける正規分布のリンク関数は単に恒等関数となります。 正規分布は平均と分散によって決まります。 平均値は平均的に期待される値、分散は平均の周りでどのくらい値がばらつくかを表す値です。 線形モデルでは、リンク関数は特徴量の重み付き和と正規分布の平均を関連付けます。
GLM のフレームワークでは、この概念は (指数型分布族に由来する) すべての分布とリンク関数に一般化されます。 y が例えば一日に飲むコーヒーの数といったような数であったなら、ポアソン分布とリンク関数である自然対数を用いたGLMでモデル化できます。
\[ln(E_Y(y|x))=x^{T}\beta\]
ロジスティック回帰モデルも二項分布を仮定した GLM で、ロジット関数がリンク関数として使われています。 ロジスティック回帰で用いられる二項分布の平均は y が 1 である確率です。
\[x^{T}\beta=ln\left(\frac{E_Y(y|x)}{1-E_Y(y|x)}\right)=ln\left(\frac{P(y=1|x)}{1-P(y=1|x)}\right)\]
そして、この式を片方が P(y=1) となるように変形すれば、ロジスティック回帰の公式が得られます。
\[P(y=1)=\frac{1}{1+exp(-x^{T}\beta)}\]
指数型分布族に属する分布は、分布から数学的に導ける正準リンク関数 (canonical link function) があります。 GLM の枠組みはその分布と関係なくリンク関数を選ぶことができます。 どうやって、適切なリンク関数を選ぶのでしょうか。 そこには、完璧なレシピはありません。 目的値の分布だけでなく、理論的な考察と実際のデータにどれだけ適合しているかを考慮に入れます。 分布の中には、正準リンク関数がその分布に対して無効であるような値につながるものもあります。 指数型分布族の分布の場合、正準リンク関数は負の逆関数であり、指数分布の領域の外側であるような負の予測値を出してしまうことがあります。 ただ、リンク関数は任意に選べるので、単純な解決策は分布の領域に適合するような別の関数を選ぶことです。
例
GLM の必要性を強調するために、一日どれくらいコーヒーを飲むかについてのデータセットについて考えてみました。 一日にコーヒーを飲む量についてのデータを集めたとします。 コーヒーが好きでないのなら、お茶でもかまいません。 コーヒーを飲んだ数とともに、現在のストレスレベル(1から10)、夜どれくらいよく眠れたか(1から10)、その日仕事があったかについて記録します。 目標は200日間のこれらのデータからコーヒーを飲んだ数を予測することです。 ストレスと睡眠については1から10まで均一の分布であり、仕事について yes/no が50%ずつとします(なんて生活でしょうか!)。 コーヒーを飲んだ数はポアソン分布に従い、\(\lambda\)(ポアソン分布の期待値)を睡眠、ストレス、仕事の特徴量の関数としてモデル化します。 この話がどうなっていくか予測できるでしょうか? 「線形モデルでこのデータをモデル化してみよう...うまくいかないなぁ...じゃあ、ポアソン分布を用いてGLMでやったらどうかな...あ!うまくいったぞ!!!!!!!」 読者のためにあまり話が逸れないようにしなければ...。
一日に飲んだコーヒーの数を目的変数としたときの分布をみてみましょう。
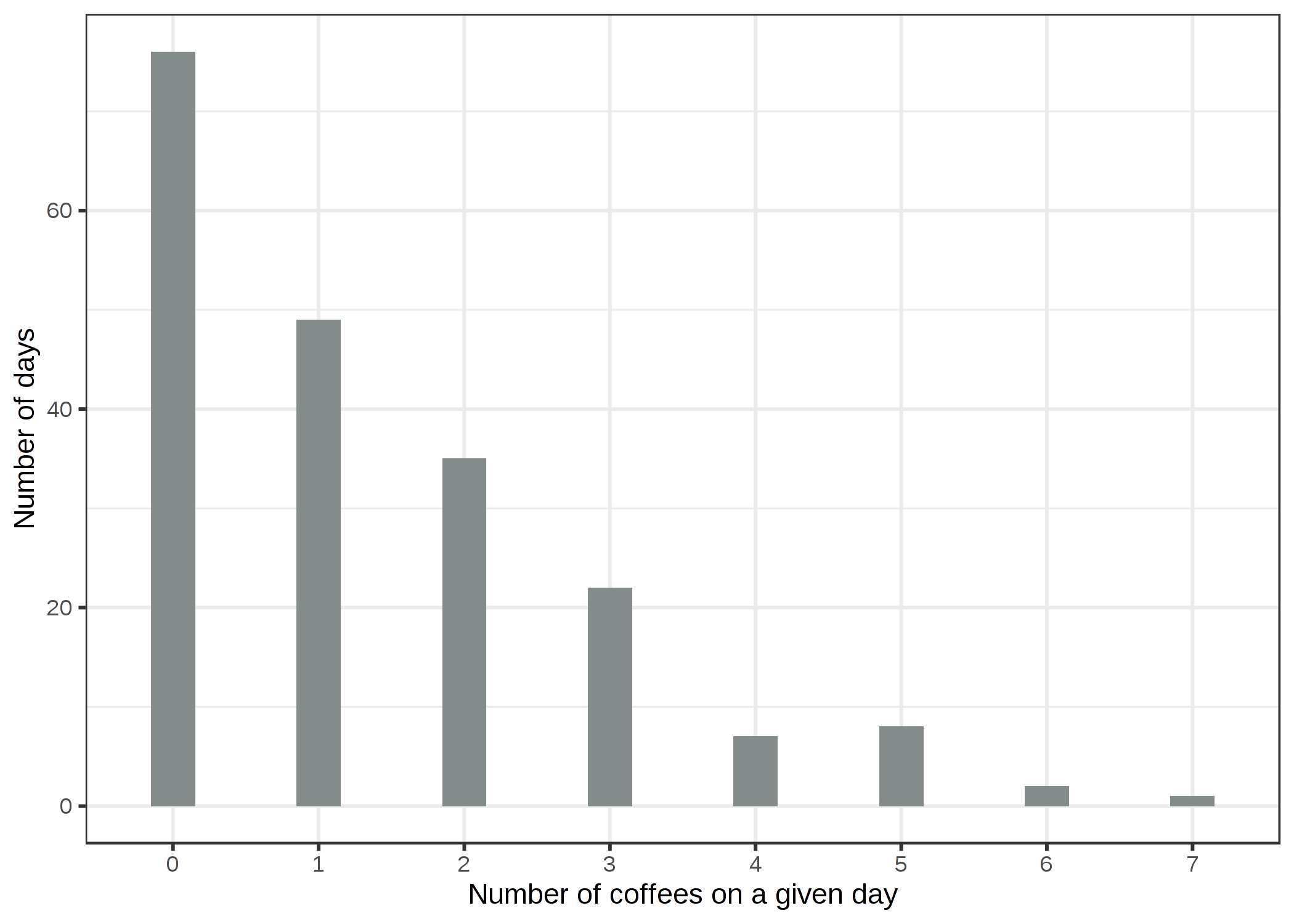
FIGURE 4.9: 200日間のコーヒーを飲んだ量の分布
76 日中 200 日はまったくコーヒーを飲んでおらず、一番飲んだ日は7 杯も飲んでいます。 愚直に線形モデルを用いて、睡眠レベル、ストレスレベル、仕事の有無の特徴量から飲んだ コーヒーの数を予測してみましょう。 誤って正規分布を仮定すると何がおかしくなるのでしょうか? 間違った仮定は推定値、特に重みの信頼区間を無効にしてしまいます。 さらに明らかな問題は、次の図に示すように予測値が真の結果の"許された"領域と合致しないということです。
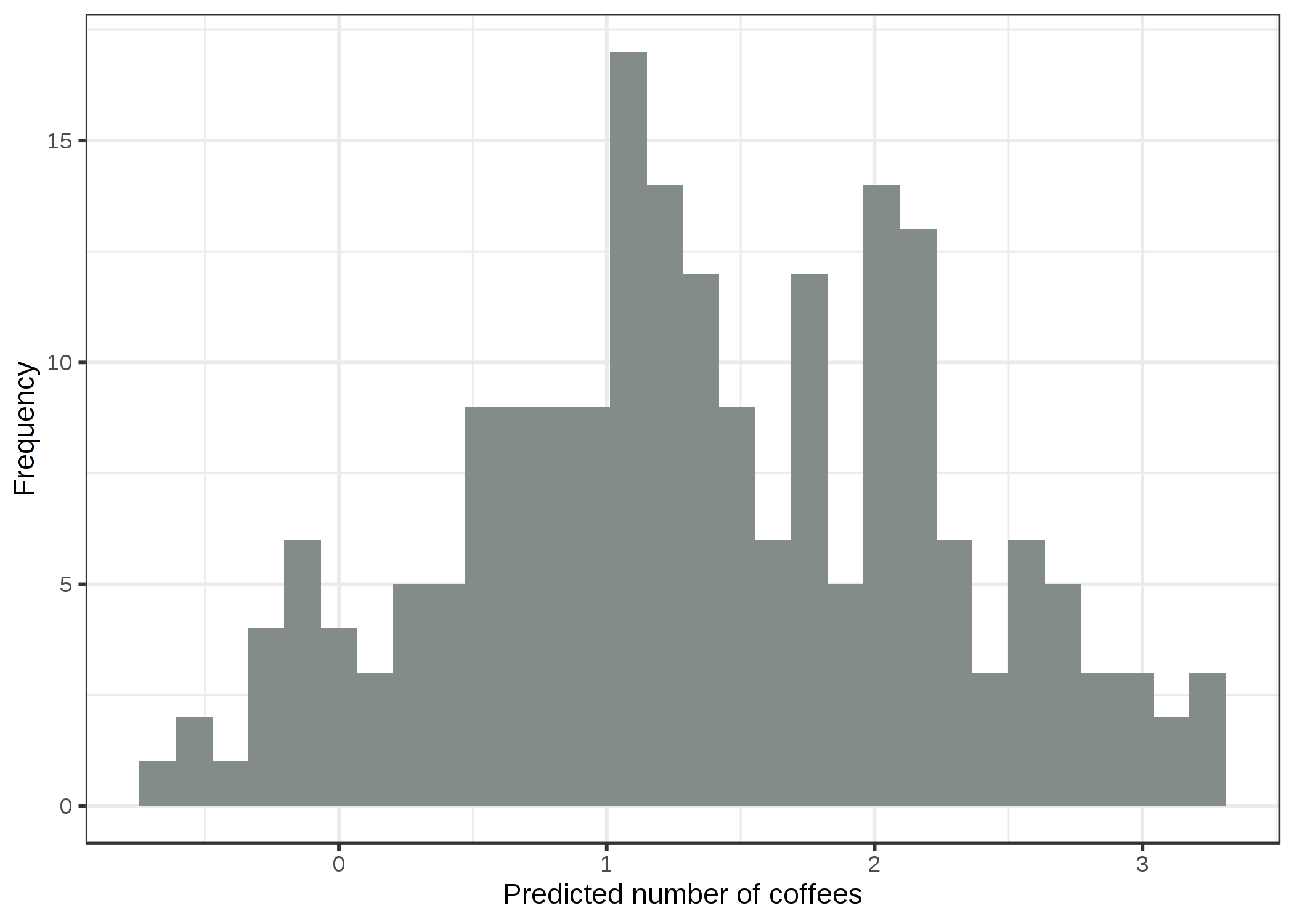
FIGURE 4.10: ストレス、睡眠、仕事に応じて予測されたコーヒーを飲む量の予測値。線形モデルは負の値を予測しています。
線形モデルは負の値を予測するので、理にかなっていません。 リンク関数と仮定している分布を変更することによって GLM ではこの問題を解決できます。 1つの選択肢は、正規分布は引き続き使い、リンク関数としては、常に正の値しか取らないようにするため、恒等関数の代わりに log-link (expの逆関数) を使用するという方法です。 さらに良いのは、データが生成されたプロセスに従った分布を選び、適切なリンク関数を選ぶことです。 結果は数ですから、ポアソン分布とリンク関数として対数関数を選ぶことが自然です。 今回は、データはポアソン分布から生成されるので、Poisson GLM はベストチョイスです。 学習された Poisson GLM による予測値の分布は次のようになります。
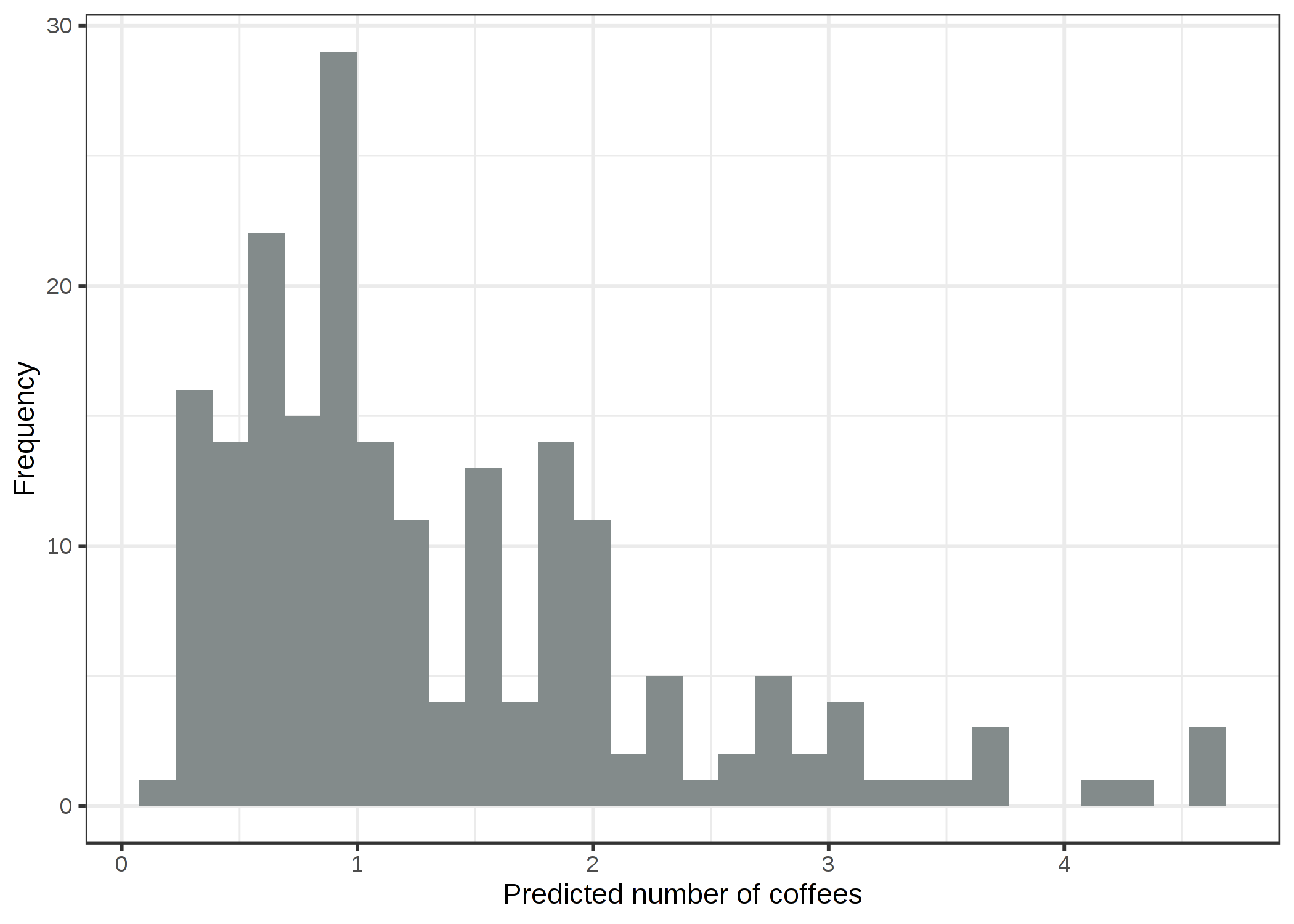
FIGURE 4.11: ストレス、睡眠、仕事に応じて予測されたコーヒーを飲む量の予測値。ポアソン分布とlog link に基づいた GLM はこのデータセットに対する適切なモデルです。
負の値を取らないので、先ほどよりも良さそうです。
GLMの重みの解釈
リンク関数と共に仮定した分布は推定される特徴量の重みがどのように解釈されるかを決めます。 コーヒーの例では、ポアソン分布とlogリンクに基づいたGLMを用いました。これによって、次のような特徴量と予測値の関係が示唆されます。
\[ln(E(\text{coffees}|\text{stress},\text{sleep},\text{work}))=\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{work}}x_{\text{work}}\]
重みを解釈するために、予測された結果の対数ではなく、リンク関数の逆関数をとり、特徴量の影響を理解しやすいように変形します。
\[E(\text{coffees}|\text{stress},\text{sleep},\text{work})=exp(\beta_0+\beta_{\text{stress}}x_{\text{stress}}+\beta_{\text{sleep}}x_{\text{sleep}}+\beta_{\text{work}}x_{\text{work}})\]
すべての重みは、指数関数の中にはいっており、exp(a + b) は exp(a) と exp(b) の積になるので、効果の解釈は加法的ではなく乗法的となります。 解釈の最後の要素は、例の実際の重みです。 以下の表に予測される重みと exp(weight) を 95% 信頼区間とともに挙げています。
| weight | exp(weight) [2.5%, 97.5%] | |
|---|---|---|
| (Intercept) | -0.16 | 0.85 [0.54, 1.32] |
| stress | 0.12 | 1.12 [1.07, 1.18] |
| sleep | -0.15 | 0.86 [0.82, 0.90] |
| workYES | 0.80 | 2.23 [1.72, 2.93] |
ストレスレベルが1点上昇すると、予測されるコーヒーの量は 1.12 倍になります。 睡眠の質が1点上昇すると、予測されるコーヒーの量は 0.86 倍になります。 仕事のある日の予測値は仕事のない日と比べて、平均して2.23倍されます。 まとめると、ストレスが多い、睡眠が少ない、仕事がある日に、より多くのコーヒーが飲まれます。
この章では正規分布にターゲットが従わない場合に有効なGLMについて少し学びました。 次は、2つの特徴量の相互作用をどのように線形回帰モデルに取り入れるかを見ていきましょう。
4.3.2 相互作用
線形回帰モデルでは、1つの特徴量がもたらす効果は他の特徴量の値とは関係がない (=相互作用がない) ことを前提としています。 しかし、多くの場合、特徴量の間には相互作用があります。 例えば、自転車レンタルの数を予測する際、気温と就業日であるかどうかの間に相互作用があるかもしれません。 おそらく、就業日であれば、何があろうとも仕事のために自転車に乗るので、気温はレンタルされる自転車の数に大して影響を与えないでしょう。 しかし休日の場合には、多くの人が娯楽目的に自転車に乗りますが、それは気温が十分に暖かいときだけでしょう。 したがって、レンタル自転車の予測では、気温と就業日の間の相互作用が期待されるかもしれません。
線形モデルで相互作用を考慮するにはどうすれば良いでしょう。 線形モデルを学習する前に、特徴量に相互作用を表現する列を追加します。 この解決策は、線形モデル自体を変更することなく、ただ列をデータに追加するだけで良いという点で優れた手法といえます。 例えば、就業日と気温の例においては、休業日の場合は 0、それ以外は気温の値を持つような特徴量を追加します。 このとき、就業日が参照カテゴリであると仮定します。 データが次のようになっているとします。
| work | temp |
|---|---|
| Y | 25 |
| N | 12 |
| N | 30 |
| Y | 5 |
以下の表は、相互作用を考慮しない場合のデータ行列を表しており、先ほどのものと少し異なります。 通常、この変換は統計ソフトウェアによって自動的に行われます。
| Intercept | workY | temp |
|---|---|---|
| 1 | 1 | 25 |
| 1 | 0 | 12 |
| 1 | 0 | 30 |
| 1 | 1 | 5 |
1列目は切片の項です。 2列目は 0 を参照カテゴリ、1 をその他としたようなカテゴリカル特徴量となっています。 そして、3列目には気温が入っています。
線形モデルで気温と就業日の相互作用を考慮したい場合、次のように相互作用の列を追加する必要があります。
| Intercept | workY | temp | workY.temp |
|---|---|---|---|
| 1 | 1 | 25 | 25 |
| 1 | 0 | 12 | 0 |
| 1 | 0 | 30 | 0 |
| 1 | 1 | 5 | 5 |
新しい列 'workY.temp' は就業日(work)と気温(temp)間の相互作用を表現します。 この列は work 特徴量が参照カテゴリ(Nである、つまり就業日でない)のときに 0 を、その他の場合には気温の値をとります。 このエンコーディングにより、線形モデルは就業日・休業日両方に対して異なる気温による線形効果を学習できます。 これが2つの特徴量間の相互作用です。 相互作用項がない場合、カテゴリカル特徴量と量的特徴量の複合効果は異なるカテゴリに対して垂直方向にシフトした直線で表現できます。 相互作用を考慮すると、量的特徴量の効果(傾き)が各カテゴリごとに異なる値を持つことができます。
2つのカテゴリカル特徴量の相互作用についても同様です。 カテゴリの組み合わせを表現する特徴量を追加します。 次の表は就業日(work)とカテゴリカルな天候(wthr)を含んだ人工的なデータです。
| work | wthr |
|---|---|
| Y | 2 |
| N | 0 |
| N | 1 |
| Y | 2 |
次に相互作用項を追加します。
| Intercept | workY | wthr1 | wthr2 | workY.wthr1 | workY.wthr2 |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
1列目は切片の計算に用いられます。 2列目はエンコードされた就業日の特徴量です。 3列目と4列目は、3つのカテゴリを持つ天候の特徴量であり、1つを参照カテゴリとして、効果を表現するためには2つの重みが必要なので、2つの列が用意されています。 残りの列は相互作用項です。 2つの特徴量の各カテゴリごと(参照カテゴリを除く)に、両方の特徴量が、あるカテゴリであれば 1 を、そうでなければ 0 を持つような列を作ります。
2つの量的特徴量に対しては、相互作用項はさらに簡単に構築できます。単に両方の特徴量の値を掛け合わせれば良いのです。
実は、自動で相互作用項を検出し追加するアプローチはいくつかあります。 そのうちの1つは、RuleFitの章で紹介されています。 RuleFit アルゴリズムでは、最初に相互作用を探索し、これらの相互作用を含めた線形回帰モデルを学習します。
例
線形モデルの章でモデル化した自転車レンタル数の予測タスクに戻りましょう。 今回は、気温と就業日の間の相互作用についても考慮します。 これにより、次の重みと信頼区間が得られます。
| Weight | Std. Error | 2.5% | 97.5% | |
|---|---|---|---|---|
| (Intercept) | 2185.8 | 250.2 | 1694.6 | 2677.1 |
| seasonSUMMER | 893.8 | 121.8 | 654.7 | 1132.9 |
| seasonFALL | 137.1 | 161.0 | -179.0 | 453.2 |
| seasonWINTER | 426.5 | 110.3 | 209.9 | 643.2 |
| holidayHOLIDAY | -674.4 | 202.5 | -1071.9 | -276.9 |
| workingdayWORKING DAY | 451.9 | 141.7 | 173.7 | 730.1 |
| weathersitMISTY | -382.1 | 87.2 | -553.3 | -211.0 |
| weathersitRAIN/... | -1898.2 | 222.7 | -2335.4 | -1461.0 |
| temp | 125.4 | 8.9 | 108.0 | 142.9 |
| hum | -17.5 | 3.2 | -23.7 | -11.3 |
| windspeed | -42.1 | 6.9 | -55.5 | -28.6 |
| days_since_2011 | 4.9 | 0.2 | 4.6 | 5.3 |
| workingdayWORKING DAY:temp | -21.8 | 8.1 | -37.7 | -5.9 |
追加した相互作用による影響は負 (-21.8) であり、95%信頼区間が 0 を含まないことからわかるように、0 から大きく離れています。 ちなみに、互いに近い日は独立でないため、データは独立同分布 (iid) ではありません。 信頼区間は誤解を招く恐れがあるため、話半分に見てください。 相互作用項は関連する特徴量の重みの解釈を変えます。 就業日であれば気温は負の効果をもたらしているでしょうか。 たとえ表が負の効果を示していたとしても、答えはノーです。 "workingdayWORKING DAY:temp" の相互作用項の重みは単独で解釈できません。 なぜなら、重みの解釈は「他のすべての特徴量を変化させずに、就業日の気温の相互作用効果を増加させると、予測される自転車の数は減少する。」となるからです。 しかし、相互作用の効果は気温による効果に追加されるだけです。 今日が就業日で、気温が1度高かったらどうなるか知りたいとします。 それなら、"temp" と "workingdayWORKING DAY:temp" の両方の重みを合計して、予測値がどれほど増加するかを判断する必要する必要があります。
相互作用は簡単に視覚化できます。 カテゴリカル特徴量と量的特徴量の間の相互作用を導入することにより、気温に対して1つではなく2つの勾配を得ることができます。 休業日('NO WORKING DAY')における気温の勾配は、表から直接読み取ることができます (125.4)。 就業日('WORKING DAY')における気温の勾配は、両方の気温の重みの合計から得られます (125.4 -21.8 = 103.6)。 'NO WORKING DAY'直線の 気温 = 0 における切片は、線形モデルの切片 (2185.8) で決定されます。 また、'WORKING DAY'直線の 気温 = 0 における切片は、線形モデルの切片 + 就業日の効果 (2185.8 + 451.9 = 2637.7) で決まります。
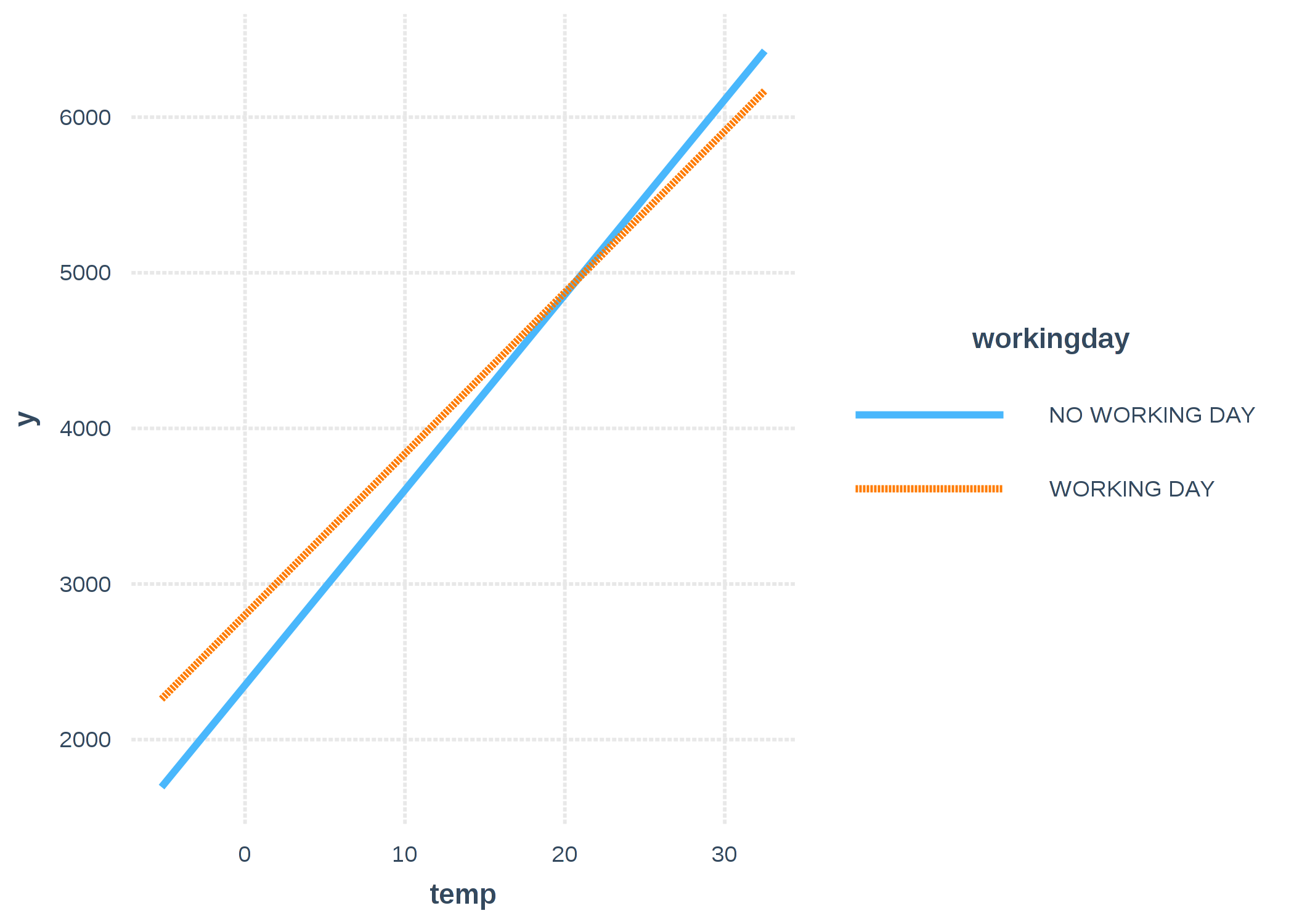
FIGURE 4.12: 線形モデルのレンタル自転車数の予測に対する気温と就業日の影響 (相互作用を含む)。就業日の各カテゴリに対して2つの気温の勾配が得られている。
4.3.3 非線形効果 - GAM
世界は線形ではありません。 線形モデルにおける線形性とは、インスタンスの特徴量の値がどのような時でも、値を 1 増やすと、常に同じ効果を予測結果に与えるということを意味します。 気温が10度から11度に上がった時と、40度から41度に上がった時とで、自転車のレンタル数に同じ影響があると考えるのは妥当でしょうか? 直感的には、気温が10度から11度に上がるとレンタル自転車数は増え、40度から41度に上がるとレンタル自転車数は減ると予想されます。これは、この本に出てくる他の例も同様です。 温度という特徴量は、レンタル自転車数に線形なプラスの影響を及ぼしますが、ある時点で平坦になり、高い温度ではマイナスの影響を及ぼします。 線形モデルはこのような影響の変化に関わらず、(ユークリッド距離を最小化することによって)あくまで最適な線形の関係性を見つけようとします。
非線形の関係は以下の手法を用いてモデル化できます。
- 特徴量の単純な変換(対数変換など)
- 特徴量のカテゴリカル化
- 一般化加法モデル(Generalized Additive Model, GAM)
それぞれの手法の詳細に入る前に、これら3つについて例を見てみましょう。 レンタル自転車のデータセットを使って、温度の特徴量のみを使用し線形モデルを学習することで、レンタル自転車数の予測をしました。 次の図はそれぞれ、標準的な線形モデル、対数変換した温度による線形モデル、温度をカテゴリカル特徴量として扱った場合の線形モデル、GAM (スプライン回帰) を使用したときの推定された勾配を示しています。
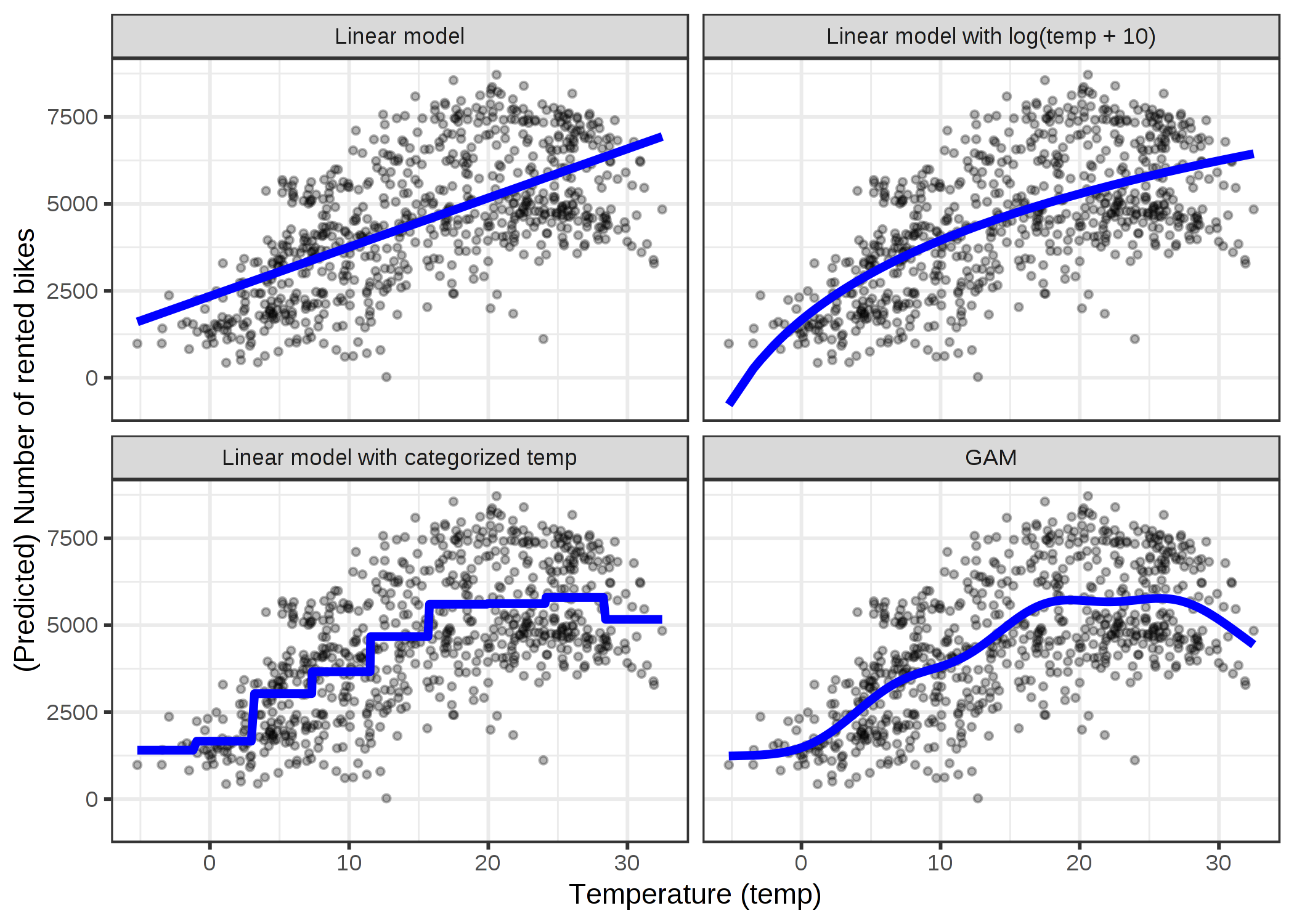
FIGURE 4.13: 温度特徴量のみを用いたレンタル自転車数の予測。線形モデル(左上)はデータにあまり適合していません。1つの解決策は、例えば対数で特徴量を変換(右上)したり、カテゴリカル化する(左下)ことですが、これは通常は悪い判断です。GAMを使うと(右下)、気温に対して滑らかな曲線を自動的に適合できます。
特徴量変換
多くの場合、特徴量の対数変換が使用されます。 対数を使用すると、10倍の温度上昇ごとに自転車の数に同じ線形効果があることが示されます。 したがって、気温が1度から10度に変化するときと、0.1度から1度に変化するときは同じ効果があります(これも間違っているように思われます)。 特徴量変換の他の例は、平方根、二乗関数、および指数関数です。 特徴量変換を使用するということは、データの特定の特徴量の列を対数などで変換したものに置き換えて、通常どおり線形モデルで学習することを意味します。 一部の統計プログラムでは、線形モデルを呼び出す時に変換方法も指定できます。 特徴量の変換は、クリエイティブな行為です。 特徴量の解釈は、選択した変換によって変わります。 対数変換を使用する場合、線形モデルにおける解釈は「特徴量の対数が1増加すると、対応する重みによって予測結果が増加する。」となります。 恒等関数ではないリンク関数でGLMを使用する場合、両方の変換を解釈に組み込む必要があるため、解釈はより複雑になります(logとexpのように互いに打ち消し合う場合は解釈は簡単なので除く)。
特徴量のカテゴリカル化
非線形効果を実現するもう1つの選択肢は、特徴量を離散化し、カテゴリカル特徴量とすることです。 たとえば、温度という特徴量をレベル[-10, -5), [-5, 0), ... の 20 の区間に分割できます。 連続値としての温度の代わりにカテゴリカル化された温度を使用する場合、各区間が独自の推定値をとるため、線形モデルはステップ関数を推定します。 このアプローチの問題は、より多くのデータが必要であり、過学習する可能性が高く、特徴量を意味のある形で離散化する方法が不明確であるということです(等距離区間または分位数?区間の数は?)。 非常に有効な場合にのみ、離散化を使用します。 たとえば、モデルを別の研究と比較できるようにするためなどです。
一般化加法モデル(Generalized Additive Models, GAM)
なぜ非線形の関係を学習のために (一般化)線形モデルを 'そのまま' 使用してはいけないのでしょうか? それがGAMの背後にある動機です。 GAMは、関係は単純な重み付き和でなければならないという制限を緩和し、各特徴量の任意の関数の総和によって結果をモデル化できると仮定します。 数学的には、GAMの関係は次のようになります。
\[g(E_Y(y|x))=\beta_0+f_1(x_{1})+f_2(x_{2})+\ldots+f_p(x_{p})\]
この式は GLM の式に似ていますが、線形項 \(\beta_j{}x_{j}\) がより柔軟な関数 \(f_j(x_{j})\) に置き換えられている点が異なります。 GAM の核は依然として特徴量効果の合計ですが、特徴量と出力の間の非線形性を許す余地があります。 線形効果もこのフレームワークでカバーされており、特徴量に対する線形性は、\(f_j(x_{j})\) を \(x_{j}\beta_j\) の形に制限することで表現できます。
大きな問題は、この非線形関数をどのように学習するかです。 その答えは「スプライン」または「スプライン関数」と呼ばれます。 スプラインは、任意の関数を近似するために組み合わせることができる関数です。 より複雑なものを構築するためにレゴブロックを積み重ねるのと少し似ています。 これらのスプライン関数を定義するには、おびただしい数の方法があります。 もしスプラインを定義するすべての方法についてもっと知りたいのなら、それは長旅になるでしょう。旅の幸運を祈っています。 ここでは詳細に立ち入らずに、直感的な説明のみに留めます。 スプラインを理解するために個人的に最も役立ったのは、個々のスプライン関数を視覚化し、データ行列がどのように変わったかを調べることでした。 たとえば、スプラインを使用して温度をモデル化するには、データから温度の特徴量を削除し、それぞれがスプライン関数を表す4つの列に置き換えます。 通常、スプライン関数はもっと多くなりますが、説明のために数を減らしました。 これらの新しいスプライン特徴量の各インスタンスでの値は、インスタンスの温度の値によって異なります。 すべての線形効果とともに、GAMはこれらのスプラインの重みも推定します。 GAMはまた、重みをゼロに近づけるためのペナルティ項も導入します。 これにより、スプラインの柔軟性が低下し、過学習が抑制されます。 曲線の柔軟性を制御するために一般的に使用される平滑化パラメータは、交差検定によって調整されます。 ペナルティ項を無視すると、スプラインを使用した非線形のモデリングは高度な特徴量エンジニアリングとなります。
GAMを使用し、温度のみから自転車の数を予測する例では、モデルの特徴量の行列は次のようになります。
| (Intercept) | s(temp).1 | s(temp).2 | s(temp).3 | s(temp).4 |
|---|---|---|---|---|
| 1 | 0.93 | -0.14 | 0.21 | -0.83 |
| 1 | 0.83 | -0.27 | 0.27 | -0.72 |
| 1 | 1.32 | 0.71 | -0.39 | -1.63 |
| 1 | 1.32 | 0.70 | -0.38 | -1.61 |
| 1 | 1.29 | 0.58 | -0.26 | -1.47 |
| 1 | 1.32 | 0.68 | -0.36 | -1.59 |
各行は、データからの個々のインスタンス (1日) を表します。 各スプラインの列には、特定の温度の値でのスプライン関数の値が含まれています。 以下に、これらのスプライン関数の様子を図示します。
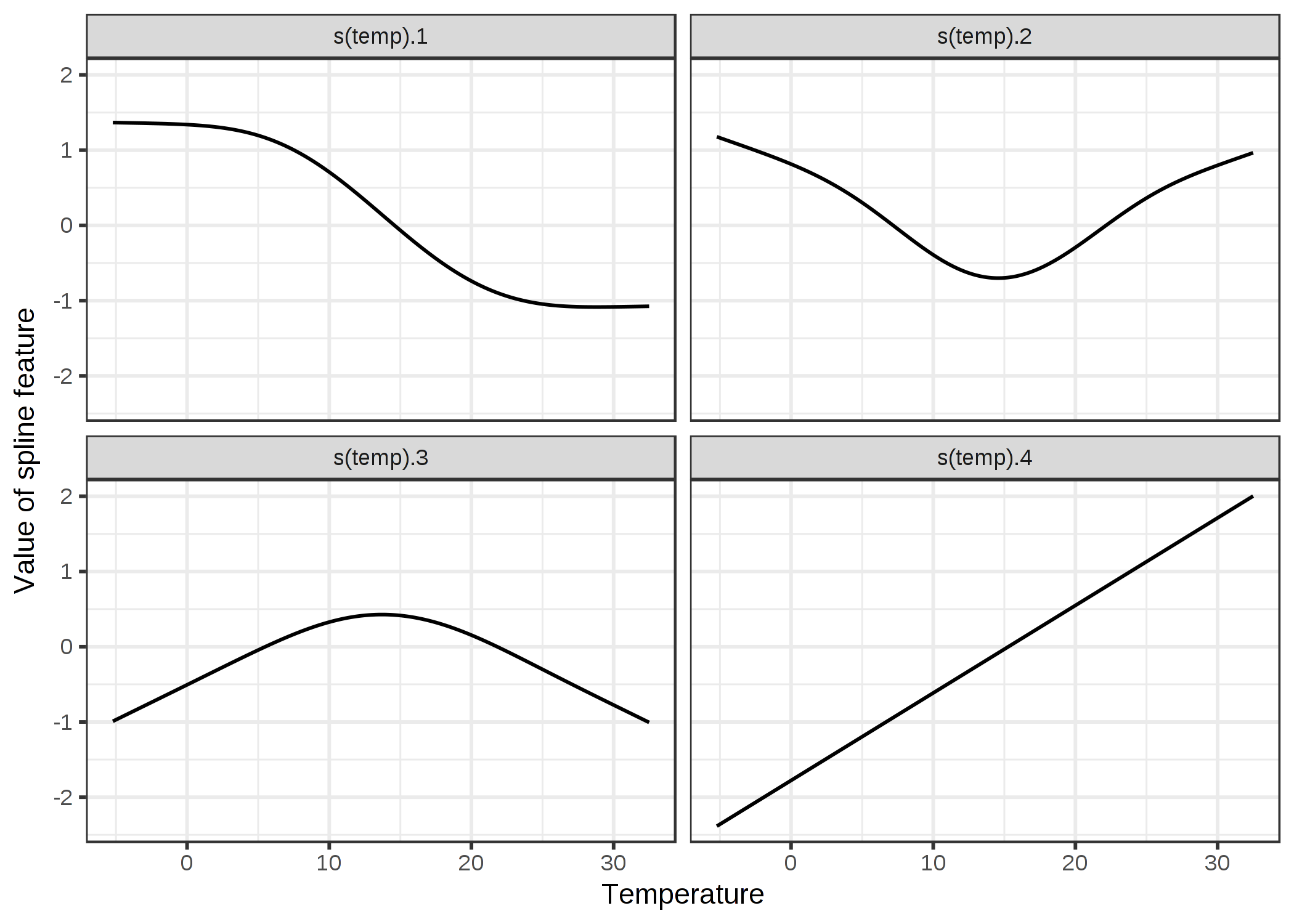
FIGURE 4.14: 温度効果を滑らかにモデル化するために、4つのスプライン関数を使用します。 各温度の値は、(ここでは)4つのスプライン値にマッピングされます。 インスタンスの温度が30度の場合、最初のスプライン特徴量の値は -1、2番目は 0.7、3番目は -0.8、および4番目は 1.7 です。
GAMは、各温度のスプライン特徴量に重みを割り当てます。
| weight | |
|---|---|
| (Intercept) | 4504.35 |
| s(temp).1 | -989.34 |
| s(temp).2 | 740.08 |
| s(temp).3 | 2309.84 |
| s(temp).4 | 558.27 |
また、推定された重みで重み付けされたスプライン関数の合計から得られる実際の曲線は、次のようになります。
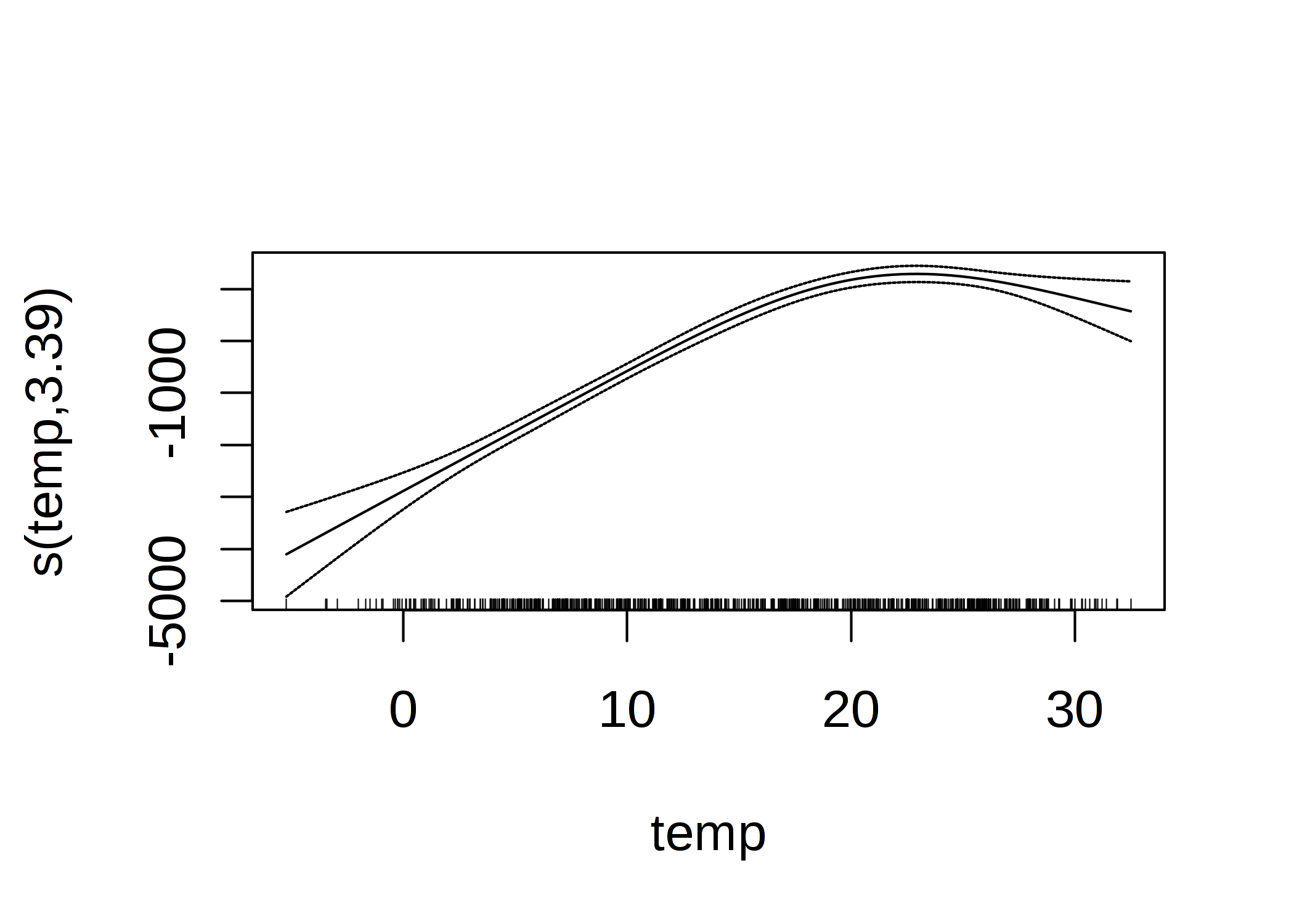
FIGURE 4.15: レンタル自転車数を予測するための温度のGAM特徴量効果(温度のみを特徴量として使用)。
滑らかな効果の解釈には、学習した曲線の視覚的なチェックが必要です。 スプラインは通常、平均予測で中心化されているため、曲線上の点は平均予測との差になります。 たとえば 0度のとき、予測される自転車の数は平均予測よりも3000台少ないということです。
4.3.4 長所
線形モデルのこれらすべての拡張は、それら自身がそれぞれ小宇宙のようなものです。 線形モデルで直面する問題が何であれ、それを修正するための拡張方法が見つかるでしょう。
ほとんどの手法は、何十年もの間使用されてきました。 たとえば、GAMはおおよそ30年前のものです。 多くの研究者や産業界の実務家は、線形モデルの経験がとても豊富であり、それらの手法はモデリング手法の現状として多くのコミュニティで受け入れられています。
それに加えて、モデルの仮定に反していないのであれば、モデルを使用して予測を行い、データに関する結論を導き出すことも可能です。 また、重みの信頼区間、有意差検定、予測区間などを得ることができます。
統計ソフトウェアは通常、GLM、GAM、およびより特別な線形モデルを学習するための非常に優れたインターフェースを備えています。
多くの機械学習モデルの不透明度は、1)スパース性の欠如、つまり多くの特徴量が使用されていること、2)非線形に扱われる特徴量、つまり効果を記述するためには1つ以上の重みが必要、および、3)特徴量間の相互作用のモデリング、の3つに起因します。 線形モデルは高い解釈可能性をもっている一方で、しばしば現実に適合しないということを前提にすれば、この章で説明した拡張は、解釈可能性をある程度維持しながら、より柔軟なモデルへのスムーズな移行を実現する優れた方法を提供しているといえるでしょう。
4.3.5 短所
利点として、線形モデルはそれぞれ独自の宇宙が広がっていると言いました。 初学者でなくても、単純な線形モデルを拡張する方法は非常に多いため圧倒されてしまいます。 実際には、研究者や実務家の多くのコミュニティが、多かれ少なかれ同じことを行う手法に独自の名前を持っているため非常にややこしく、複数の並行宇宙があると言えます。
線形モデルの修正により、そのほとんどのモデルは解釈性が低下します。 恒等関数以外の任意のリンク関数 (GLMにおいて) は、解釈を複雑にしますし、 相互作用も解釈を複雑にします。 また、非線形の特徴量の効果は、直感的ではないか(対数変換のように)、あるいは、もはや単一の数値で要約できなくなります(スプライン関数など)。
GLM や GAM などは、データの生成プロセスに関する仮定に依存しています。 それらの仮定に反した場合、重みの解釈に妥当性はなくなります。
ランダムフォレストや勾配ブースティングなどの決定木ベースのアンサンブル学習モデルは、多くの場合、最も洗練された線形モデルよりも優れたパフォーマンスを示します。 これは、私自身の経験からもいえますし、kaggle.com などのプラットフォームで優勝したモデルの結果からもいえます。
4.3.6 ソフトウェア
この章のすべての例は R 言語を用いて作られています。 GAM には gam パッケージが使用されていますが、それ以外にも多くのパッケージがあります。 R には回帰モデルを拡張する驚くほど多くのパッケージがあります。 他の分析用の言語にも負けることはなく、R は、他の考えられる線形モデルの拡張の原点と言えます。 Python でも様々な実装を見つけることができ、pyGAM は GAM の Python 実装ですが、これはまだ成熟していません。
4.3.7 さらなる拡張
約束通り、線形モデルを使う際に遭遇する可能性のある問題と、検索したら解決できるように解決方法の名前をリストで示します。
データが独立同分布 (iid) の仮定に反する場合。
例として、同じ患者の繰り返しの測定がこれに当たります。
このような場合は、混合モデル (mixed models)や一般化推定方程式 (generalized estimating equations)で検索してください。
モデルが不均一な分散の誤差持つ場合。
例として、住宅価格を予想する時、高価な住宅であるほど、予測値の誤差は大きくなりますが、これは線形モデルの等分散性に反します。
ロバスト回帰 (robust regression)で検索してください。
モデルに大きく影響する外れ値がある場合。
ロバスト回帰 (robust regression)で検索してください。
イベントが起きるまでの時間を予測したい場合。
イベントまでの時間のデータでは、大抵、打ち切られた測定値が含まれていますが、これはイベントが起きるまでに十分な時間が無かったことを意味しています。 例えば、ある会社が二年間のデータしか与られていない状態で、製氷機の故障を予測したい場合です。 二年経過しても故障しない機械もありますが、その後故障する可能性もあります。
パラメトリック生存モデル (parametric survival models)、コックス回帰 (cox regression)、 生存時間分析 (survival analysis)で検索してください。
予測の結果がカテゴリカルの場合。
もし、結果が2つのカテゴリの場合、ロジスティック回帰モデルを使用してカテゴリの確率を求めることができます。 さらに多くのカテゴリがある場合、multinomial regressionで検索してください。
ロジスティック回帰と multinomial regression はどちらも GLM です。
順序付きのカテゴリを予測したい場合。
例えば学校の成績です。
比例オッズモデル (proportional odds model)で検索してください。
結果が、家族の中の子供の数のようなカウントの場合。
ポアソン回帰 (Poisson regression)で検索してください。 ポアソンモデルもGLMです。
0 の値の頻度がとても多いという問題があるかもしれません。 そのときは、ゼロ過剰ポアソン回帰 (zero-inflated Poisson regression)やHurdleモデル (hurdle model)で検索してください。
正しい因果関係を導き出すためにどの特徴量をモデルに含めればいいのかわかりません。
例えば、血圧に効果のある薬が知りたいときです。 薬はなんらかの血液量に直接影響を与え、この血液量が結果に影響を与えます。 血液量を回帰モデルに含めるべきでしょうか?
因果推論 (causal inference)や媒介分析 (mediation analysis)で検索してください。
データに欠損値がある場合。
多重代入法 (multiple imputation)で検索してください。
事前知識をモデルに取り入れたい場合。
ベイズ推定 (Bayesian inference)で検索してください。
最近少し元気がありません。
"Amazon Alexa Gone Wild!!! Full version from beginning to end"で検索してください。