5.2 Individual Conditional Expectation (ICE)

Individual Conditional Expectation (ICE) plots は、ある特徴量が変化したときにそのインスタンスの予測がどのように変化するかを1本の線で可視化する手法です。

特徴量の平均的な効果に関する partial dependence plot は、特定のインスタンスではなく、全体的な平均に注目しているため、大域的な方法と言えます。個々のインスタンスに対する PDP と等価な手法は、individual conditional expectation (ICE) plot (Goldstein et al. 2017²⁹) と呼ばれています。 ICE plot はインスタンスごとの、ある特徴量が予測に与える影響を別々に可視化します。 partial dependence plotでは、全体に対して1本の線で表現していましたが、ICE plot では、1つのインスタンスにつき1本の線で表現されます。 PDP は ICE plot の線を平均したものと一致します。ある線(とそれに対応するインスタンス)における値は、他の全ての特徴量を一定に保ったまま、ある特徴量の値をグリッド上の別の値に置き換えて、いくつかの新しいインスタンスを作成し、それらに対してブラックボックスモデルで予測をすることで計算されます。その結果は、グリッド上の特徴量の値と、それぞれの予測値を持つインスタンスに対する点の集合です。

PDP の代わりに個々の予測を見るポイントは何でしょうか。 PDP は相互作用によって生まれる不均一な関係を見えなくしてしまうことがあります。 PDP は特徴量と予測が平均的にどんな関係にあるかを示していますが、これは、対象の特徴量と他の特徴量との相互作用が弱い場合にのみ有効です。相互作用がある場合、ICE plot はより多くの洞察を与えてくれるでしょう。

より正式な定義は次のとおりです。 ICE plot では、\(\{(x_{S}^{(i)},x_{C}^{(i)})\}_{i=1}^N\) 内のそれぞれのインスタンスにおいて、曲線 \(\hat{f}_S^{(i)}\) は \(x^{(i)}_{S}\) に対して、\(x^{(i)}_{C}\) が固定されたままプロットされます。

5.2.1 例

子宮頸がんのデータセットを使って、それぞれのインスタンスで「年齢」の特徴量がどれだけ影響を与えているかを見てみましょう. リスクのある要因が与えられたとき女性ががんになる確率を予測するランダムフォレストを分析してみます。 Partial dependence plot では、50歳周辺でがんの確率が増加しているのが見受けられますが、データセット内のすべての女性に対して当てはまるのでしょうか。 ICE plot は、ほとんどの女性にとって、年齢的な影響は50歳で確率が増加するという平均的なパターンに従っているが、例外もあるということを明らかにしています。若いときから高確率を予測されている女性は、予測されるがん確率は年齢によってあまり変わりません。

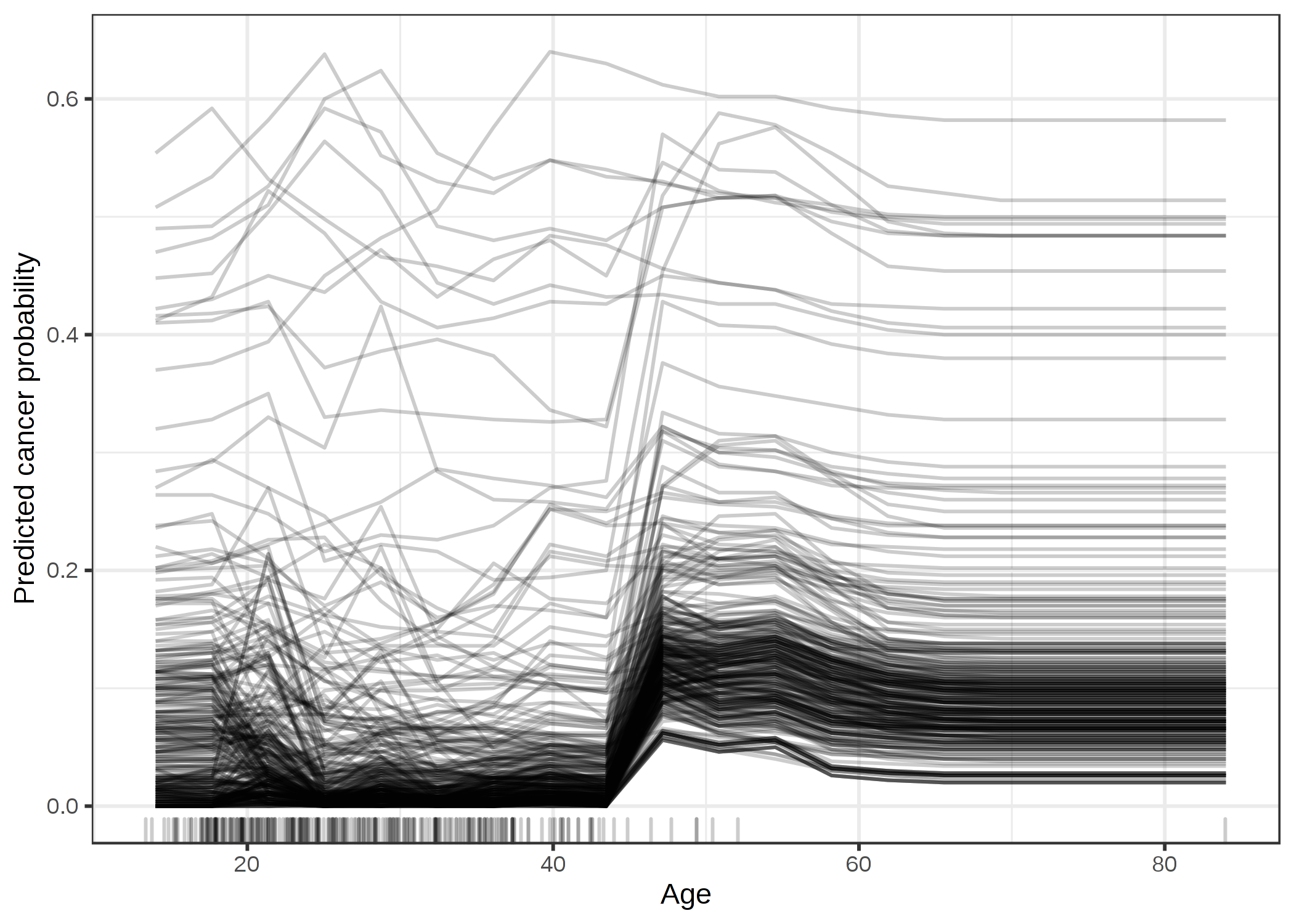
FIGURE 5.6: 年齢ごとの子宮頸がんの確率のICEプロット。それぞれの線は一人の女性を表す。ほとんどの女性は、年齢の増加に伴って、がんと予測される確率が増加する。予測の確率が 0.4 を超える女性に対しては、年齢が高くなっても予測はあまり変化しない。

次の図は、自転車レンタル予測に対する ICE プロットです。ここでも使用されている予測モデルはランダムフォレストです。

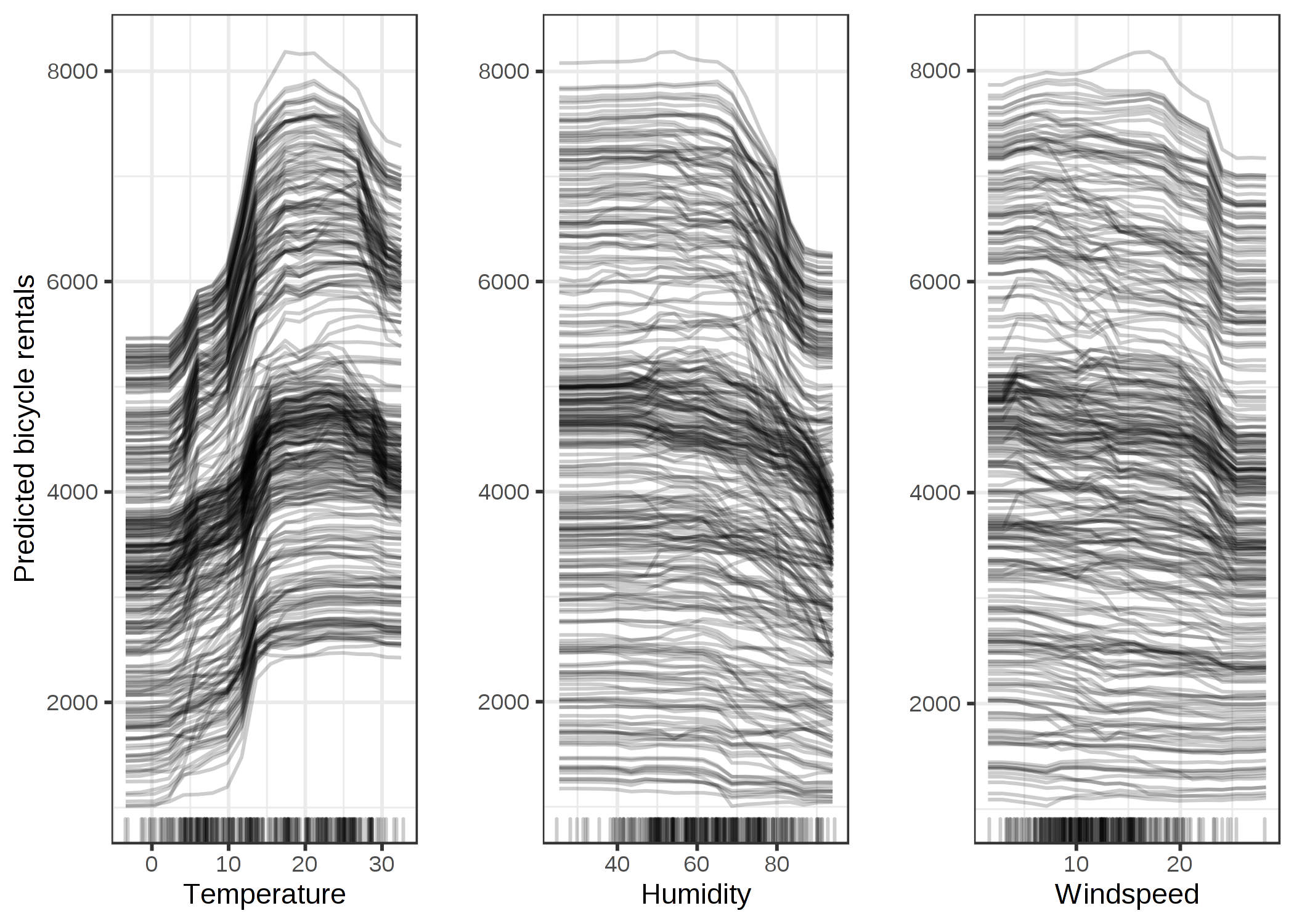
FIGURE 5.7: 天候ごとの自転車レンタル予測の ICE プロット。PDP のときと同様の効果が見られる。

全ての曲線は同じコースを辿っているように見えるので、明らかな相互作用はないと言えます。つまり、PDP は表示された特徴量と予測された自転車の数との関係の優れた要約となっていると言えます。

5.2.1.1 Centered ICE Plot

ICE プロットには問題があります。 ICE 曲線は異なる予測から始まるため、個々の間で ICE 曲線が異なるかどうかを判断するのが難しい場合があります。簡単な解決策は、特徴量の特定の点で曲線を中央に配置し、この点との予測の差のみを表示することです。結果のプロットは、centered ICEプロット（c-ICE）と呼ばれています。特徴量の下端にカーブを固定することをお勧めします。新しい曲線は次のように定義されます。

\[\hat{f}_{cent}^{(i)}=\hat{f}^{(i)}-\mathbf{1}\hat{f}(x^{a},x^{(i)}_{C})\]

ただし、\(\mathbf{1}\) は適切な数(普通、1 か 2)だけ 1 が並んだベクトルであり、\(\hat{f}\) は学習されたモデルで、x^a はアンカーポイントです。

5.2.1.2 例

例えば、年齢に対して子宮頸がんの ICE プロットを作成し、観測された最も若い年齢を中心に線を引いてみましょう。

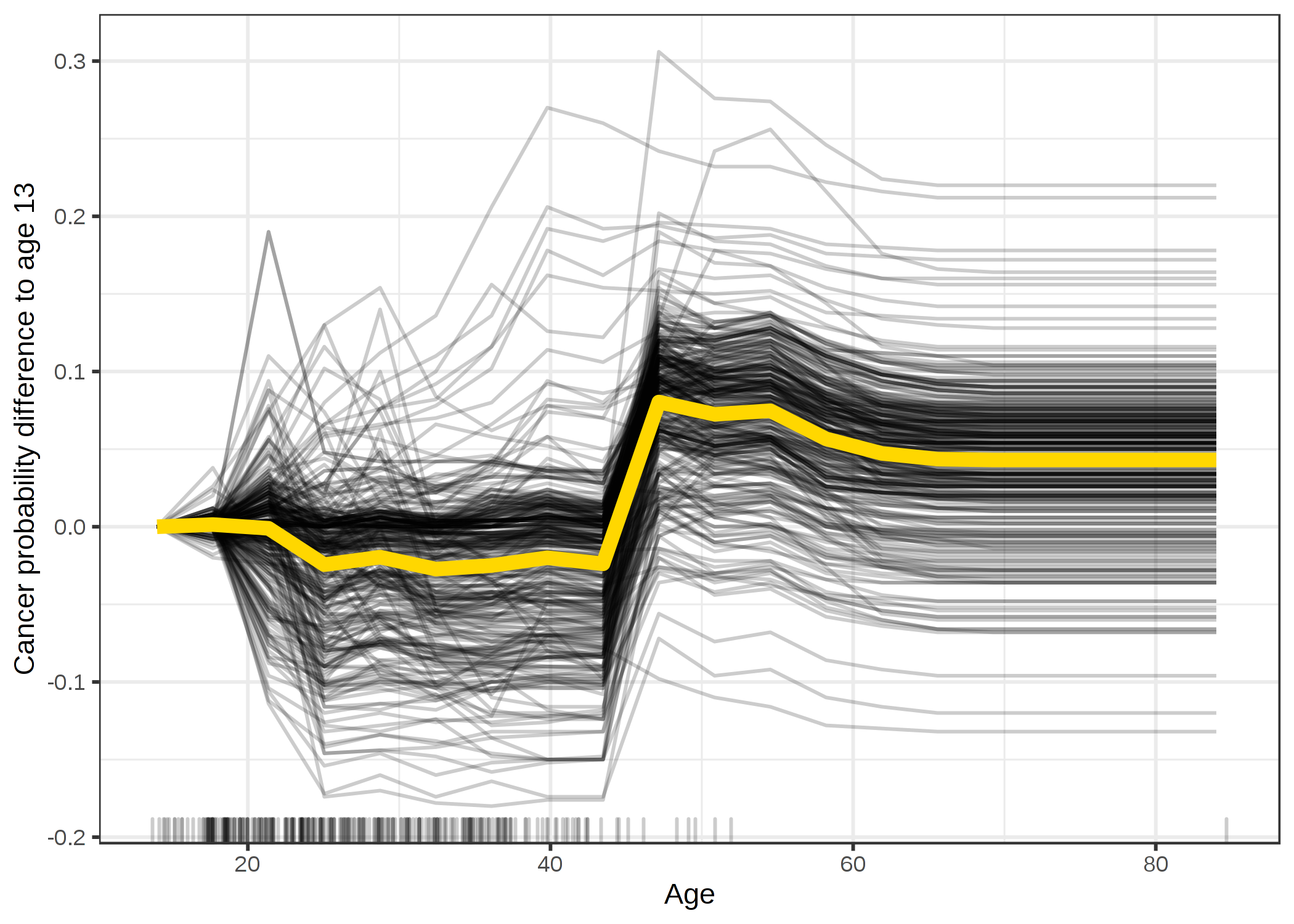
FIGURE 5.8: 年齢ごとに予測されたがんの確率に対する centered ICE プロット。線は年齢 14 が 0 に固定されている。年齢 14 に比べ、ほとんどの女性の予測は、予測確率が増加する45歳まで変化しない。

Centered ICE プロットでは、個々のインスタンスの曲線の比較を簡単にできます。これは、予測値の絶対的な変化ではなく、特徴量の範囲の固定点と比較した予測の差を確認したい場合に役立ちます。

自転車レンタル数予測の例で、centered ICE プロットをみてみましょう。

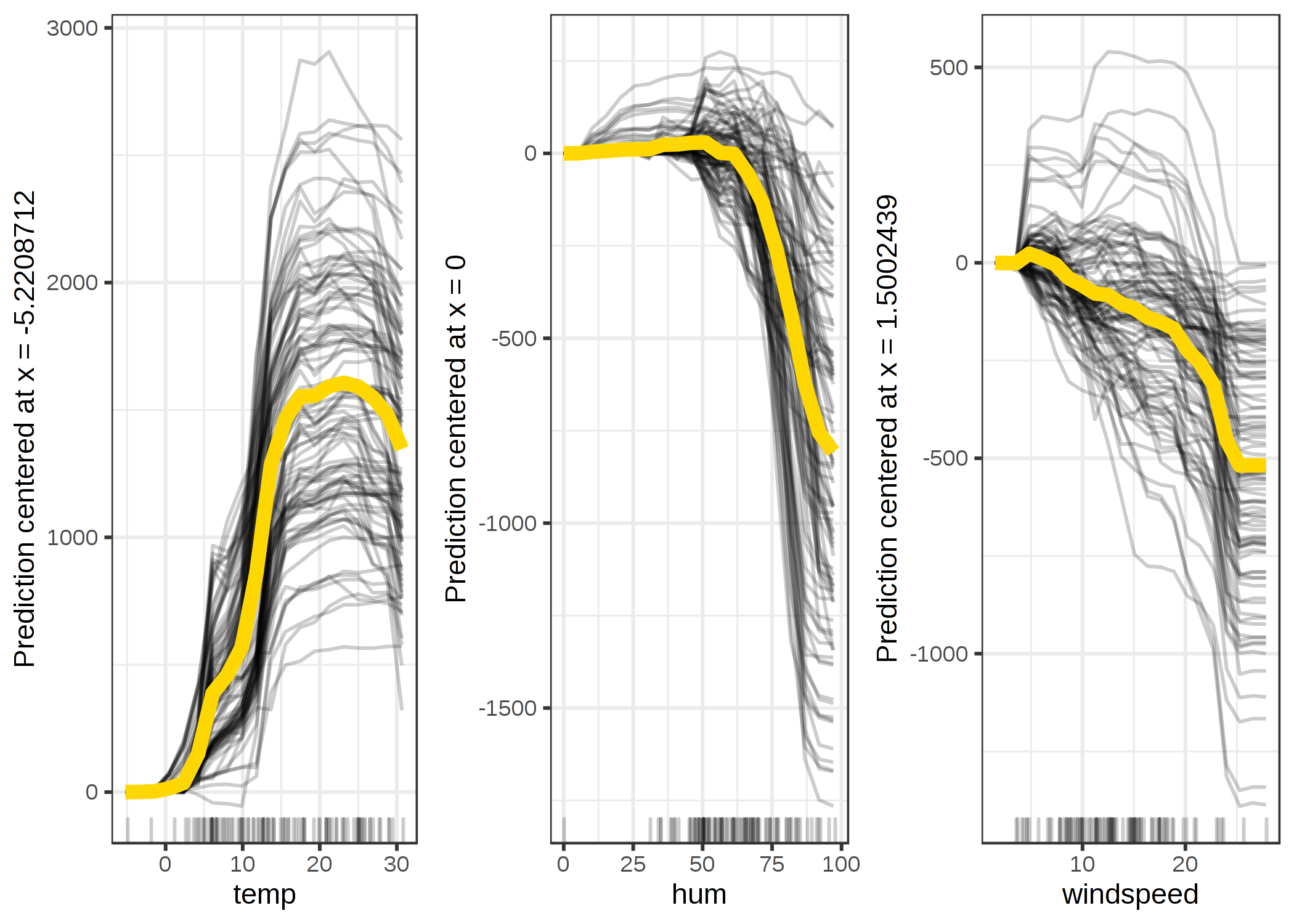
FIGURE 5.9: 天候による予測された自転車レンタル数の centered ICE プロット。線は、観測された特徴量の最小値での予測との差を示している。

5.2.1.3 Derivative ICE Plot

不均一性を簡単に視覚化するための別の方法は、特徴量に関して、予測関数の個々の微分を見ることです。結果のプロットは derivative ICE plot (d-ICE)と呼ばれています。関数の微分(または、曲線)は、変化が起きたのか、また、どの方向に起きたのかを教えてくれます。 Derivative ICE plot を用いると、（少なくとも一部の）インスタンスでブラックボックスの予測が変化する特徴値の範囲を簡単に見つけることができます。もし、注目している特徴量 \(x_S\) と他の特徴量 \(x_C\) の間に相互作用がないのであれば、予測関数は以下のように表現できます。

\[\hat{f}(x)=\hat{f}(x_S,x_C)=g(x_S)+h(x_C),\quad\text{with}\quad\frac{\delta\hat{f}(x)}{\delta{}x_S}=g'(x_S)\]

相互作用がないとき、個々の偏微分は全てのインスタンスで同じである必要があります。もし、これらが異なる場合は相互作用が原因であり、d-ICE plot を用いて可視化できます。微分の標準偏差を示すことは、推定された微分に不均一性がある S の特徴量の領域を強調するのに役立ちます。ただし、derivative ICE plot は計算に長い時間がかかるため、現実的ではないかもしれません。

5.2.2 長所

ICE 曲線は partial dependence plot よりも直感的に理解可能です。 1つの線は、1つのインスタンスに対して、対象の特徴量を変化させたときの予測を表します。

Partial dependence plot とは異なり、ICE 曲線は不均一な関係性を明らかにできます。

5.2.3 短所

ICE 曲線は1つの特徴量のみを意味のある形で表示できます。2つの特徴量を使うと、いくつかの重複した面を描画する必要があるため、このプロットをみても何も理解できないでしょう。

ICE 曲線は、PDP と同様の問題に直面します。興味のある特徴量が、その他の特徴量と相関している場合、同時分布によって、線の中のいくつかの点は妥当でないデータ点となる可能性があるということです。

多くの ICE 曲線が描かれたとき、プロットは激しく重なり合い、何も発見できません。解決方法は、線に透明度を追加するか、線のうちのいくつかのみを描画することです。

ICE 曲線の中で、平均をみることは簡単ではないかもしれません。これに対する単純な解決方法は、ICE 曲線と PDP を組み合わせることです。

5.2.4 ソフトウェアと代替手法

ICE plots は、iml（これらの例で使用）、ICEbox [^ ICEbox]、および pdp の R パッケージで実装されています。 ICE にとても類似しているもう1つのRパッケージは condvisです。

Goldstein, Alex, et al. "Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation." Journal of Computational and Graphical Statistics 24.1 (2015): 44-65.↩