5.6 グローバルサロゲート (Global Surrogate)

グローバルサロゲートモデル (global surrogate model) は、ブラックボックスモデルの予測を近似するよう学習された解釈可能なモデルです。 サロゲートモデルを解釈することによって、ブラックボックスモデルについて結論を導き出せます。 機械学習をさらに活用して、機械学習の解釈性を解決するのです。

5.6.1 理論

サロゲートモデルは、工学の分野でも用いられています。 興味のある結果を得るのが高価であったり時間がかかったり、そもそも計測が困難である場合 (複雑なコンピュータシミュレーションに依存するなど) には、代わりに安価で高速なサロゲートモデルの結果で代替されます。 工学の分野で用いられるサロゲートモデルと解釈可能な機械学習で用いられるサロゲートモデルの違いは、モデルはシミュレーションではなく、解釈可能な機械学習モデル (シミュレーションではなく) あるということです。 (解釈可能な) サロゲートモデルの目的は、元のモデルの予測をできるだけ正確に近似し、同時に解釈可能にすることです。 サロゲートモデルのアイデアは様々な名称として見つけることができます。 近似モデル、メタモデル、応答曲面モデル、エミュレータなど。

実は、サロゲートモデルを理解するために必要な理論はあまりありません。 ブラックボックスモデルの予測関数 f を、解釈可能という制約の元、サロゲートモデルの予測関数 g でできるだけ正確に近似したいというだけのことなのです。 関数 g は任意の解釈モデルで利用できます。 -- 例えば、interpretable models chapter -- で紹介されているものが使えます。

線形モデルについて、g は以下のように表せます。

\[g(x)=\beta_0+\beta_1{}x_1{}+\ldots+\beta_p{}x_p\]

決定木について、g は以下のように表せます。

\[g(x)=\sum_{m=1}^Mc_m{}I\{x\in{}R_m\}\]

サロゲートモデルの学習は、ブラックボックスモデルの内部の情報を必要とせず、データと予測関数へのアクセスのみアクセスできれば良いので、モデル非依存の手法と言えます。 元の機械学習モデルが他のものと変わったとしても、引き続きサロゲート手法を利用できます。 ブラックボックスモデルの種類とサロゲートモデルの選択は切り離されているのです。

以下の手順を実行することで、サロゲートモデルを得ます。

  1. データセット X を選択します。 これはブラックボックスモデルを学習するのに使用したものと同じデータセット、もしくは、同じ分布の他のデータセット。アプリケーションに応じてデータの部分集合やデータの一部を選択できます。
  2. 選択されたデータセット X について、ブラックボックスモデルの予測値を取得します。
  3. 解釈可能なモデル(線形モデル、決定木など)を選択します。
  4. データセットXと予測値に基づいて解釈可能なモデルを学習します。
  5. おめでとうございます、これでサロゲートモデルを取得できました。
  6. サロゲートモデルがブラックボックスモデルの予測をどの程度再現できているのかを測定します。
  7. サロゲートモデルを解釈します。

あるサロゲートモデルのアプローチには、追加のステップが存在していたり、多少の差はあったりするかもしれませんが、一般的な考え方はここで説明されている通りです。

サロゲートモデルがブラックボックスモデルをどの程度再現しているのかを計測する方法の1つに R2 スコアがあります。

\[R^2=1-\frac{SSE}{SST}=1-\frac{\sum_{i=1}^n(\hat{y}_*^{(i)}-\hat{y}^{(i)})^2}{\sum_{i=1}^n(\hat{y}^{(i)}-\bar{\hat{y}})^2}\]

ここで、\(\hat{y}_*^{(i)}\) はサロゲートモデルのi番目のインスタンスの予測値で、\(\hat{y}^{(i)}\) はブラックボックスモデルの予測値、\(\bar{\hat{y}}\) はブラックボックスモデルの予測値の平均です。 SSE は二乗誤差の総和 (Sum of Squares Error)、SST は二乗の総和 (Sum of Squares Total)です。 R2 の尺度はサロゲートモデルによって捉えられた分散の割合として解釈できます。 もし、R2 が 1 に近い (SSE が低い) 時、解釈可能モデルはブラックボックスモデルの挙動を非常によく近似できているということになります。 したがって、R2 が 1 に近い場合 (SSE が低い)、複雑なモデルを解釈可能なモデルに置き換えたほうが良いかもしれません。 また、R2 が0に近い (SSE が高い)時、解釈可能なモデルはブラックボックスモデルの説明に失敗しているということになります。

ここで、ブラックボックスモデルの性能自体、つまり実際の結果とブラックボックスモデルの予測の良し悪し には言及していないことに注意してください。 ブラックボックスモデルの性能は、サロゲートモデルの学習の成否と関係がありません。 サロゲートモデルの解釈は、現実世界に対してではなくモデルについて解釈するため有効です。 しかし、ブラックボックスモデルの性能が悪ければブラックボックスモデル自体が無意味になるので、当然サロゲートモデルの解釈は無意味になります。

また、元のデータの一部や、インスタンスに重み付けしたものに対してもサロゲートモデルを作ることも有効です。 その場合、サロゲートモデルの入力の分布は変化しているので、どこに注目して解釈するのかが変わります (なので、グローバルではなくなります) 。 データの特定のインスタンスに従って局所的に重み付けすると (あるインスタンスが選択されたインスタンスに近いほど重みが大きいなど)、個々のインスタンスの予測を説明できる局所的なサロゲートモデルを得られます。 ローカルなモデルについては次の章で詳しく解説しています。

5.6.2 例

サロゲートモデルを実演するために回帰と分類の例について考えてみましょう。

最初に、天気とカレンダーの情報が与えられたときの 1日の自転車のレンタル数を SVM で予測するため学習します。 SVMは解釈性が高くないので、決定木 (CART) を解釈可能なサロゲートモデルとして学習し、SVM の挙動を近似します。

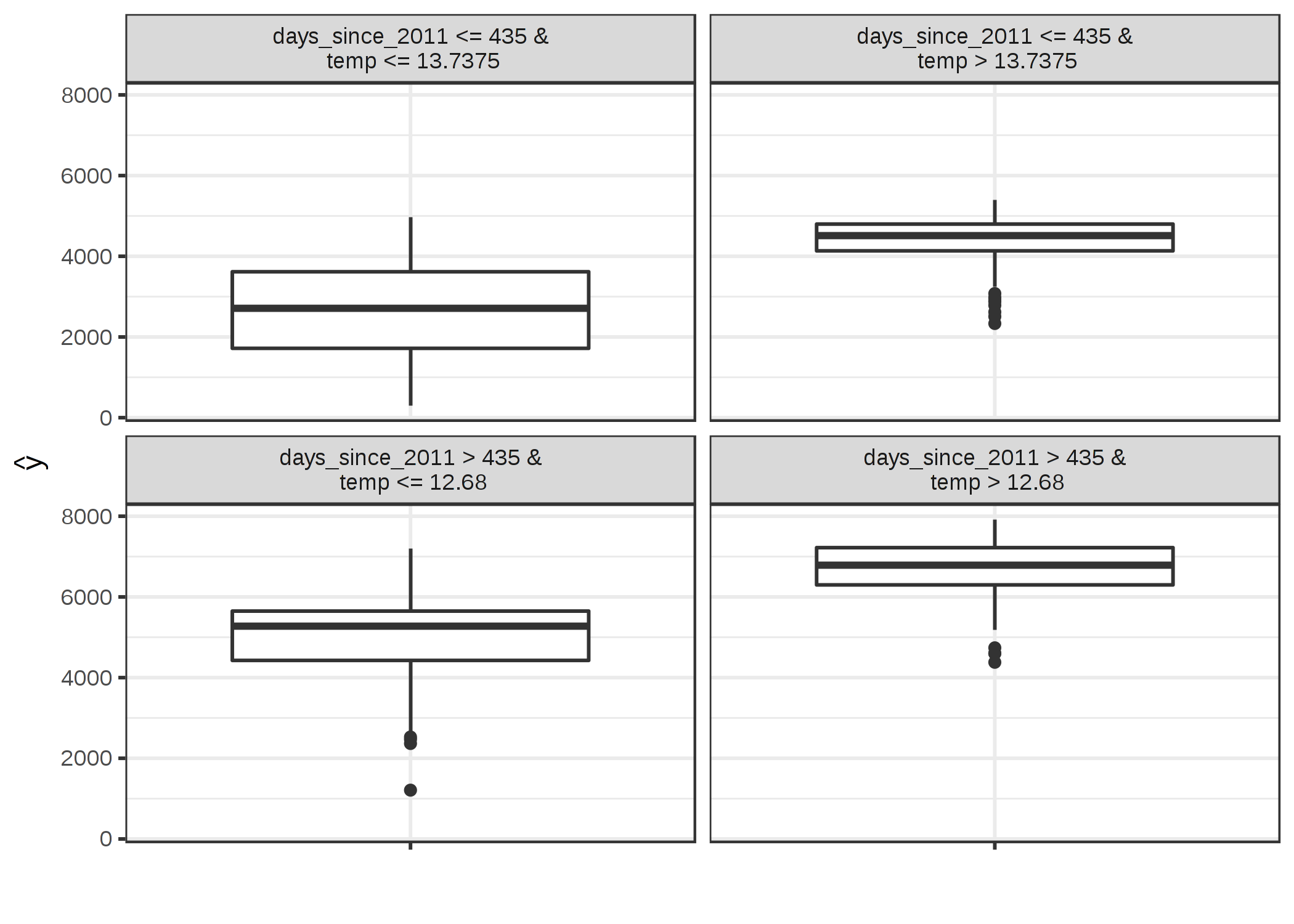
自転車のレンタルデータセットで学習した SVM の予測を近似したサロゲートモデルの木の終端ノード。ノード内の分布を確認すると、2年後以降 (カットポイントは435日) の気温が13度を超える時にサロゲートモデルが自転車のレンタル数が多くなると予測している。

FIGURE 5.30: 自転車のレンタルデータセットで学習した SVM の予測を近似したサロゲートモデルの木の終端ノード。ノード内の分布を確認すると、2年後以降 (カットポイントは435日) の気温が13度を超える時にサロゲートモデルが自転車のレンタル数が多くなると予測している。

このサロゲートモデルの R2 スコア (因子寄与) は 0.77 であり、これは元のブラックボックスの挙動を非常に良く近似していることを示していますが、ただし完全ではありません。 もし、これが完璧なら、SVM を捨てて、代わりに決定木を使うことができます。

2つ目の例として、ランダムフォレストを用いて子宮頸がんの確率を予測します。 ここでも元のデータセットを用いて決定木を学習しますが、データからの実際のクラス (健康なクラスとがんのクラス) の代わりに、ランダムフォレストの予測を結果として用います。

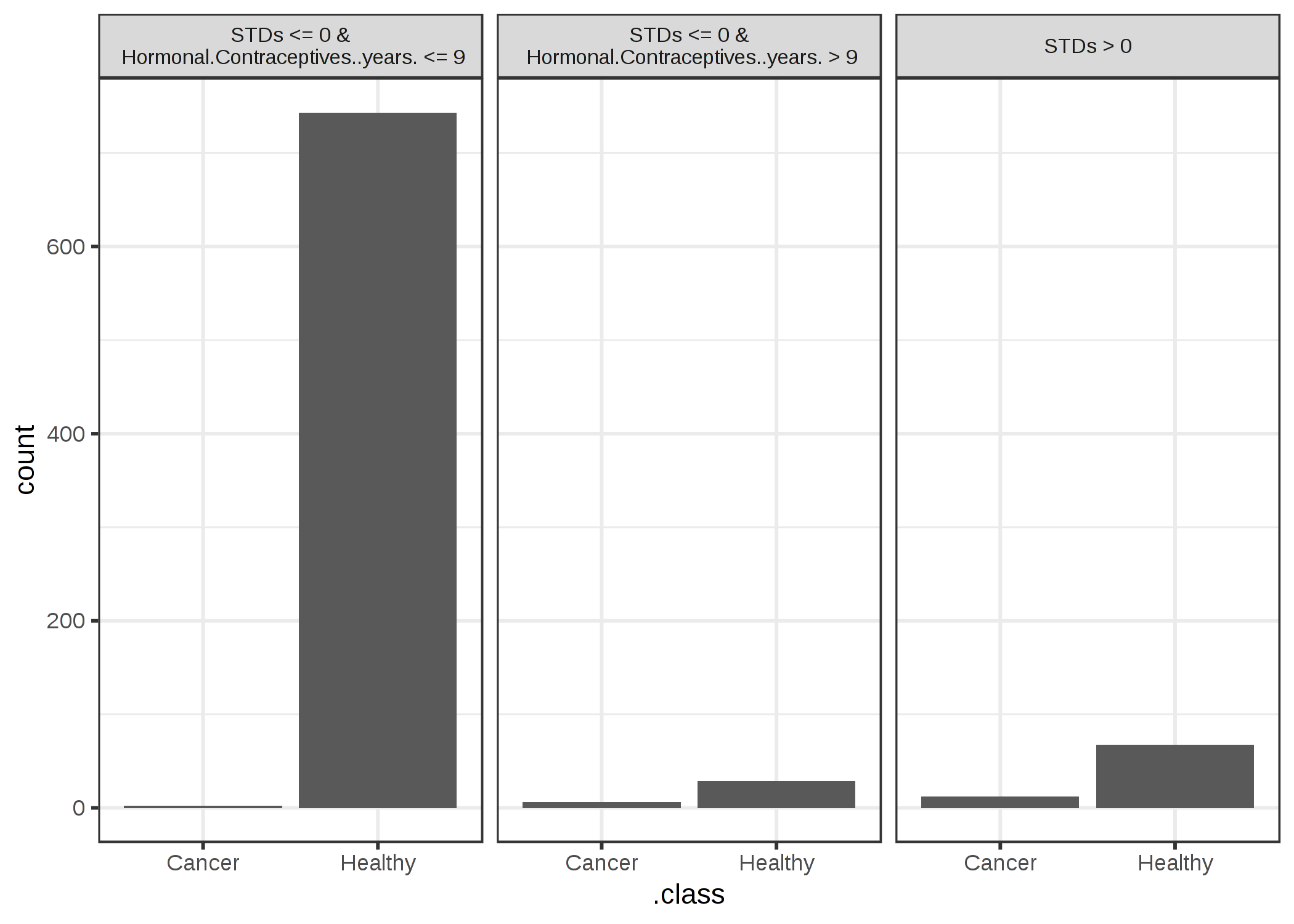
子宮頸がんのデータセットで学習されたランダムフォレストの予測を近似するサロゲートモデルの木の終端ノード。ノード内のカウントはノード内でのブラックボックスモデルの分類の頻度を表す。

FIGURE 5.31: 子宮頸がんのデータセットで学習されたランダムフォレストの予測を近似するサロゲートモデルの木の終端ノード。ノード内のカウントはノード内でのブラックボックスモデルの分類の頻度を表す。

このサロゲートモデルの R2 スコア(因子寄与)は 0.19 であり、これはランダムフォレストをうまく近似していないことを示しています。そのため、複雑なモデルについての結論を出す時にこの木の学習結果を使用すべきではありません。

5.6.3 長所

サロゲートモデルの手法は柔軟です。 解釈可能なモデルの章のモデルならどのようなモデルでも使用できます。 これは、また、解釈可能なモデルだけでなく、ブラックボックスモデルでも使用できることを意味します。 あなたは、いくつかの複雑なモデルを作って、それをあなたの会社の異なるチームに説明することを想定してください。 あるチームは線形モデルに精通し、もう一方は決定木が理解できるとしましょう。 あなたは、元のブラックボックスモデルに対して、2つのサロゲートモデルを学習し、2種類の説明を提示できます。 もし、より性能の良いブラックボックスモデルを見つけたとしても、同じクラスのサロゲートモデルを使うことができるので解釈手法を変更する必要はありません。

私はこの手法が、とても直感的でストレートだと考えています。 つまり、実装しやすいことだけでなくデータサイエンスや機械学習に関わりのない人にも説明しやすいということです。 R2 スコアを用いると、サロゲートモデルがブラックボックスモデルの予測をどの程度、近似できているか簡単に計測できます。

5.6.4 短所

サロゲートモデルは実際の結果を見ていないので、 データではなくモデルについての結論を出していることに気をつける必要があります。

サロゲートモデルがブラックボックスモデルを十分近似しているかを示す最良のR2 スコアの閾値は明らかではありません(ばらつきの 80% が説明されることでしょうか？それとも 50% や 99% でしょうか？)。

サロゲートモデルがブラックボックスモデルにどれだけ近いかを計測できます。 近すぎないが、十分近くにいると仮定してみましょう。 データセットの一部では非常に近いが別の部分に対しては大きく乖離しているということが起こり得ます。 この場合、単純なモデルの解釈は全てのデータ点に対して等しく優れているとは言えません。

解釈可能なモデルとして選んだサロゲートモデルには長所と短所が存在します。 一般的に、本質的に解釈可能なモデル(線形モデルや決定木も含む)は存在せず、解釈可能であるという幻想を抱くことは危険ですらあると主張する人もいます。 あなたがこの意見に共感しているのであれば、当然この手法はあなたの求めるものではありません。

5.6.5 ソフトウェア

例では R パッケージの iml を使用しました。 機械学習モデルを学習できるのであれば、自分自身でサロゲートモデルを実装できるはずです。 単に、ブラックボックスモデルの予測値を予測する解釈可能なモデルを学習するだけです。