5.1 Partial Dependence Plot (PDP)
Partial dependence plot (PDP, PD plot) は1つ、または2つの特徴量が機械学習モデルの予測結果に与える周辺効果 (marginal effect) を示します(J. H. Friedman 200127)。 Partial dependence plot は入力と出力の関係が線形か、単調か、より複雑かどうかを表現できます。 例えば、線形回帰モデルに適用した場合、partial dependence plot は常に線形の関係を示します。
回帰に対する Partial dependence 関数は以下のように定義されます。
\[\hat{f}_{x_S}(x_S)=E_{x_C}\left[\hat{f}(x_S,x_C)\right]=\int\hat{f}(x_S,x_C)d\mathbb{P}(x_C)\]
\(x_S\) は partial dependence 関数をプロットするべき特徴量で、\(x_C\) は機械学習モデル \(\hat{f}\) のそのほかの特徴量を表します。 通常、集合 S の中には、1つか2つの特徴量が含まれます。 S の中の特徴量が、予測に与える効果を知りたい対象となります。 特徴ベクトル \(x_S\) と \(x_C\) を組み合わせて、特徴空間 x を構成します。 Partial dependence は、集合 C の中の特徴量の分布に対して機械学習モデルの出力を周辺化することで機能します。これによって、この関数は集合 S の中の関心のある特徴量と予測結果との関係を示すことができます。 他の特徴量に対して周辺化することによって、S の中の特徴量にのみ依存する関数を得ることができ、他の特徴量との相互作用も含まれます。
Partial function \(\hat{f}_{x_S}\) は学習データの平均として計算されます。これはモンテカルロ法としても知られています。
\[\hat{f}_{x_S}(x_S)=\frac{1}{n}\sum_{i=1}^n\hat{f}(x_S,x^{(i)}_{C})\] Partial function は 特徴量 S の与えられた値に対して、予測に対する平均的な周辺効果 (average marginal effect) が何であるかを示しています。 この式中の、\(x^{(i)}_{C}\) は関心のない特徴量に対するデータセットからの実際の値であり、n はデータセットに含まれるインスタンスの数を表しています。 PDP の仮定は、C の中の特徴量は、S の中の特徴量と相関していないということです。もし、この仮定が成り立たなければ、PDP に対して計算された平均は、とても起こりそうにない、もしくは不可能なデータ点が含まれてしまいます。(短所を参照)
機械学習モデルが確率を出力する分類の場合、partial dependence plot は、S の特徴量に異なる値が与えられた特定のクラスの確率を表示します。 複数のクラスを扱うときの簡単な方法は、クラスごとに1本の線またはプロットを描くことです。
PDP はグローバルな方法です。 この方法は全てのインスタンスを考慮し、特徴量と予測結果のグローバルな関係についてのステートメントを提供します。
カテゴリカル特徴量
これまでは、数値の特徴量のみを想定していました。 カテゴリカル特徴量に対しては、 partial dependence はとても簡単に計算できます。 カテゴリのそれぞれに対して、全てのインスタンスを強制的に同じカテゴリとすることで、 PDP を計算できます。 例えば、自転車レンタルのデータセットに関して、季節に関する partial dependence plot に興味があるとすると、各季節に 1 つずつで、合計 4 つの数値が得られます。 “夏”の値を計算するためには、全てのデータの季節を”夏”に置き換えて、予測の平均を求めます。
5.1.1 例
実用上は、特徴量の集合 S は通常ただ1つ、もしくは多くても2つの特徴量のみを持たせます。なぜなら、1つの特徴量のとき2次元のプロットになり、2つの特徴量の場合は3次元のプロットになるからです。 2次元の紙やモニター上に3次元を描くことがすでに挑戦的なので、これ以上は、非常に扱いにくくなります。
ある日に借りられる自転車の数を予測する回帰の例に戻りましょう。 今回は、自転車の数を予測するためにランダムフォレストを用いて学習し、モデルが学習した関係性を可視化するために partial dependence plot を利用しました。
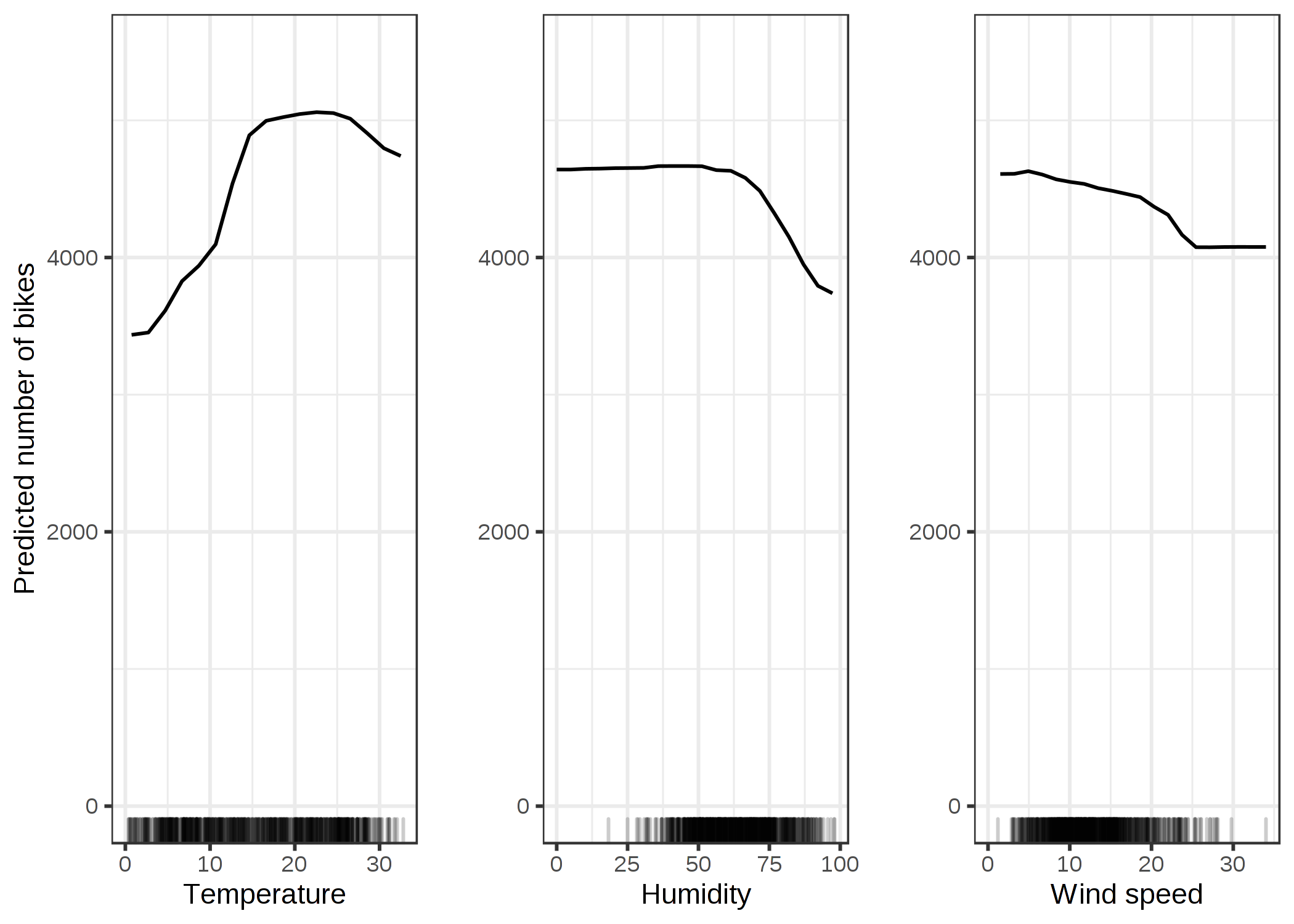
FIGURE 5.2: 自転車レンタル予測モデルの気温、湿度、風速に対するPDP。 気温で最も違いが見られ、暑くなればなるほど、自転車はレンタルされる。この傾向は20度まで上昇し、平坦になり、30度で少し減少する。x軸上のマークはデータの分布を示している。
暖かいが暑すぎない場合、モデルは平均して、多くの自転車がレンタルされると予測します。 湿度が 60% を超えると、自転車のレンタルは抑制されます。 それに加えて、風が吹けば吹くほど自転車に乗りたがる人は少なくなっていますが、これは理にかなっています。 興味深いことに、風速が 25km/h から 35km/h へ増加する間は、自転車の利用予測数は下降していません。しかし、これは十分な学習データが無いために、この範囲において機械学習モデルが意味のある予測を学習できなかったためかもしれません。 少なくとも直感的には、特に風速が非常に高い場合は、自転車の数が減ると考えられます。
カテゴリカル特徴量の partial dependence plot を例示するために、自転車レンタルにおける季節の特徴量の効果を調べます。
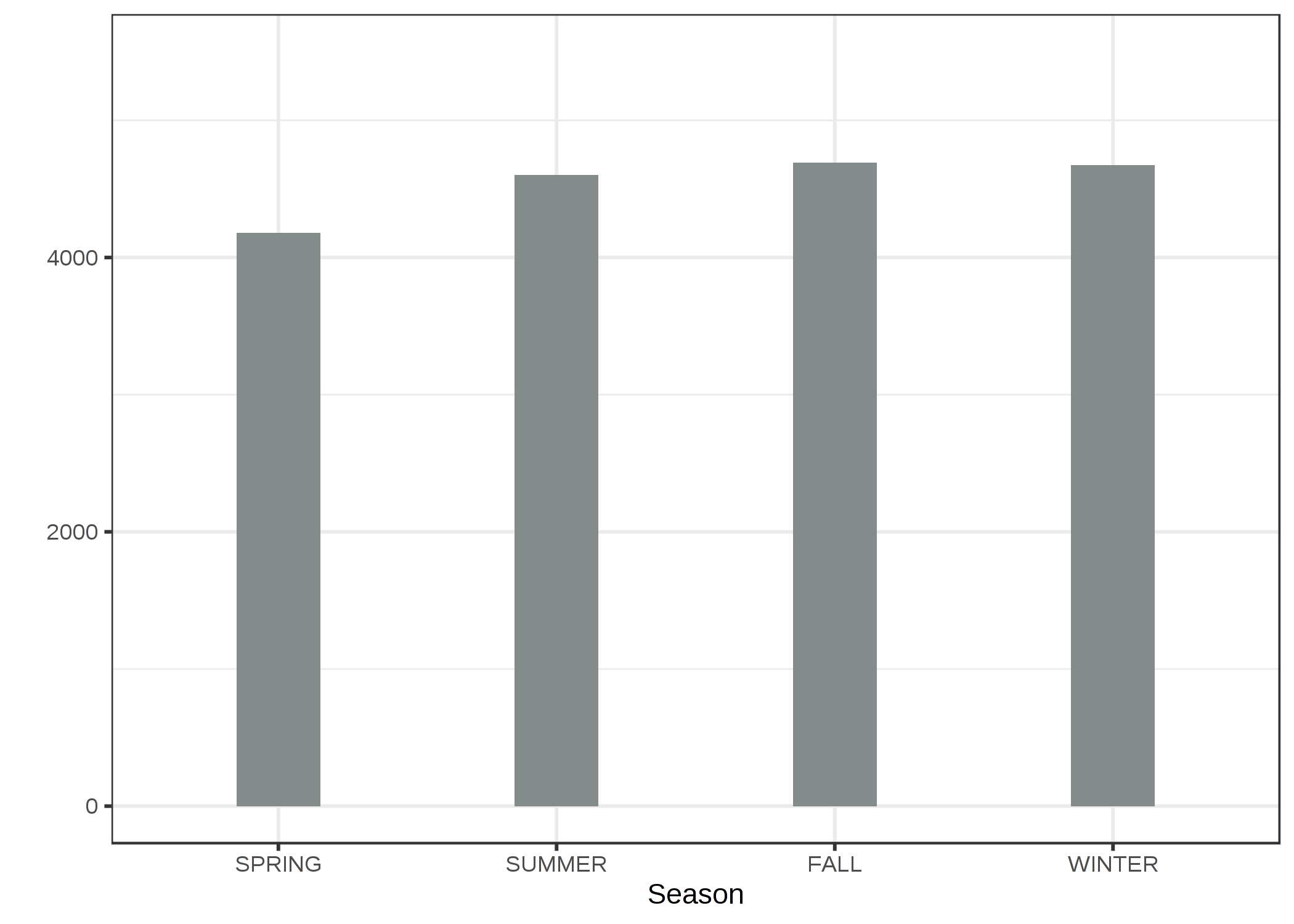
FIGURE 5.3: 季節に関する自転車レンタル予測モデルの PDP。 予想外にも全ての季節で同様の効果があることがわかった。ただし、春は自転車レンタル数のモデルの予測結果が小さかった。
Partial dependence を子宮頸がん分類についても計算してみます。 リスク要因に基づき女性が子宮頸がんにかかるか否かを予測するためにランダムフォレストを用いて学習しました。 ランダムフォレストでのがんにかかる確率と様々な特徴量との関係について、partial dependenceを計算し可視化します。
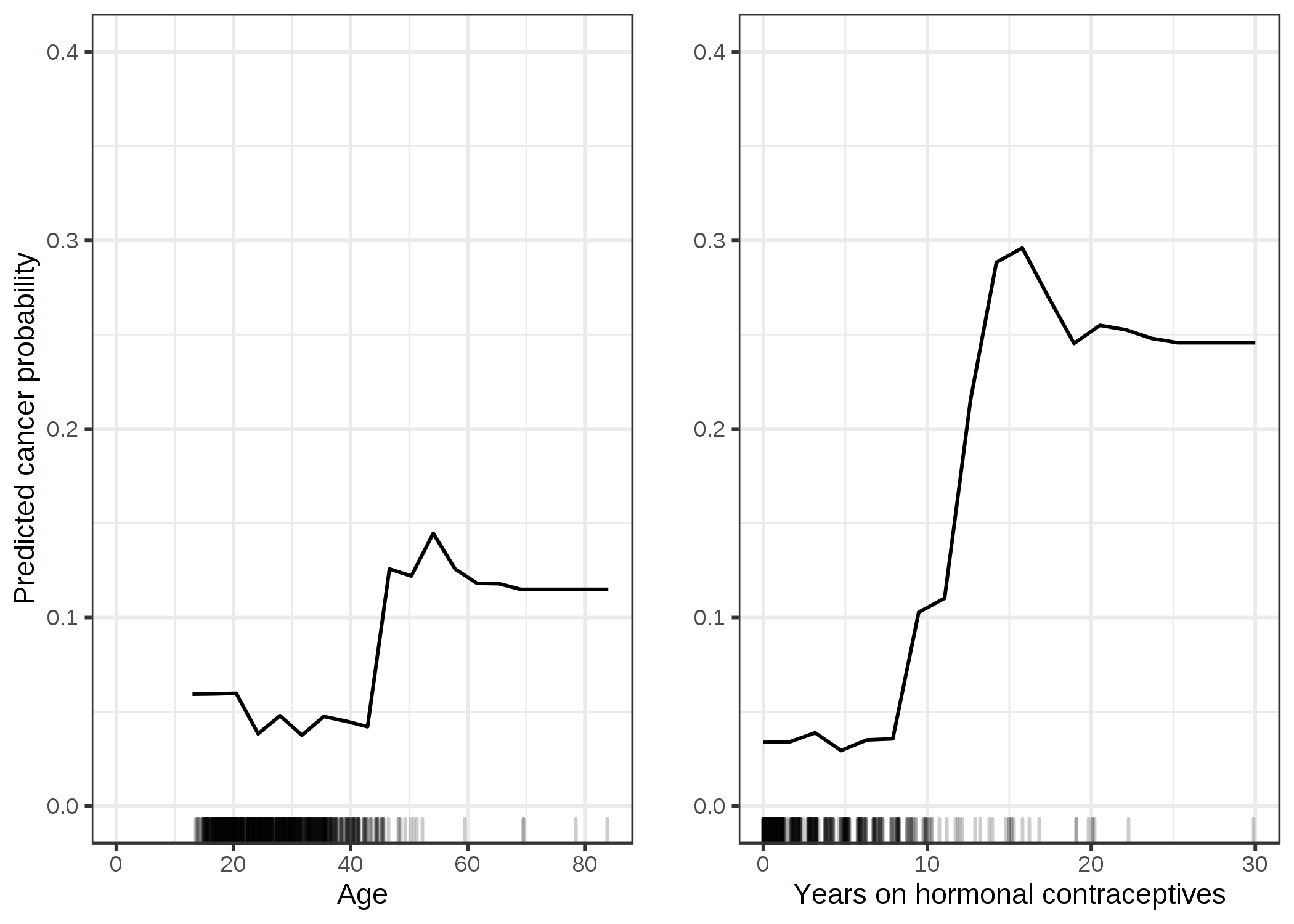
FIGURE 5.4: 年齢とホルモン避妊薬の使用年数に基づいたがんの確率のPDP。年齢に対して、40歳まで確率が低く、それ以降は確率が増加することをPDPは示している。ホルモン避妊薬の使用年数が増加すればするほど、特に、10年を境に、予測されたがんのリスクも高くなる。どちらの特徴量も大きな値の付近では十分な数のデータ点を使用することができなかったので、この付近における推定結果の信頼性は低いことに注意。
2つの特徴量について、一度に partial dependence を可視化できます。
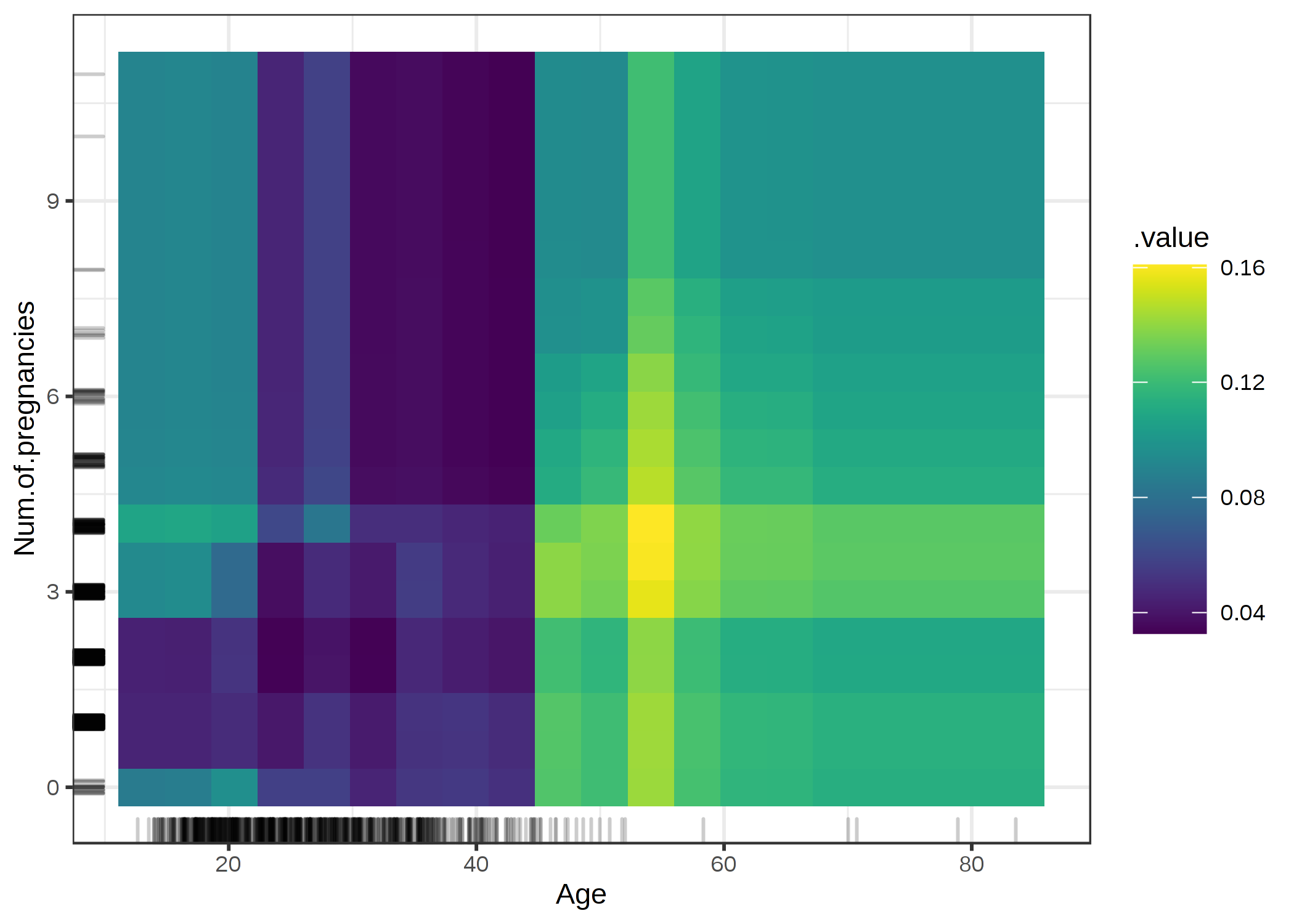
FIGURE 5.5: 年齢と妊娠回数の相互作用とがんの確率のPDP。図は45のときにがんの確率が増加することを示している。25歳以下で妊娠回数が1または2回のときは、0回もしくは2回より多い場合と比較して予測されたがんのリスクは低かった。ただし、これは因果ではなく、単なる相関関係の可能性があるので、結論を出すときは注意。
5.1.2 長所
Partial dependence plot の計算は直感的です。 ある特徴量の値での partial dependence 関数は、全てのデータ点が特定の特徴量の値を持つと仮定した場合の予測の平均を表しています。 私の経験上、専門家ではない人たちも PDP のアイデアをすぐに理解できます。
もし、PDP を計算した特徴量が他の特徴量と相関していなかったのなら、PDP は完璧に、特徴量が平均的に予測にどのような影響を与えているかを表しています。 相関関係がない場合、説明は明快です。 Partial dependence plot は、j 番目の特徴量が変わった時に、あなたのデータセット内の予測値の平均がどう変化するのかを示します。 ただし、特徴量が相関している時、もっと複雑になります。詳しくは、短所の方をみてください。
Partial dependence plot は、実装が簡単です。
Partial dependence plot の計算には、因果関係の解釈があります。 特徴量に介入を行い、予測の変化を計算しています。 これは、特徴量と予測結果の因果関係を分析していることになります。28 出力を特徴量の関数として明示的にモデル化していることから、この関係性はモデルに関する因果関係であるが、必ずしも現実世界の因果関係ではないということに注意してください。
5.1.3 短所
Partial dependence 関数で確かめることができる現実的な最大特徴量の数 は2です。 これは PDP の問題ではなく、2次元の表現(紙やスクリーン)と我々が3次元以上をうまく想像できないことが原因です。
PDP の中には 特徴量の分布 を示さないものもあります。 分布を省くのは誤解を招くおそれがあります、なぜならほとんどデータがない部分を深読みしすぎてしまう可能性があるからです。 この問題は、ラグ(x軸上のデータ点を示す)またはヒストグラムを表示することで簡単に解決できます。
独立性の仮定が PDP の最大の問題です。 Partial dependence が計算される特徴量が他の特徴量と相関していないと仮定します。
例えば、体重と身長が与えられ、ある人が歩く速さを予測したいとしましょう。 その中の1つの特徴量 (身長) の partial dependence を調べるために、もう1つの特徴量(体重)が身長と相関がないと仮定しますが、それは明らかに間違った仮定です。 特定の身長 (例: 200cm) の PDP の計算のために、体重の周辺分布の平均を計算しますが、このとき 50kg 以下のデータも含まれます。これは2メートルの人にとっては現実的ではありません。
言い換えると、特徴量同士が相関していると、現実的にとても低い確率でしか起こらないような新しいデータ点をつくってしまうことになります (例えば、2メートルの身長で 50kg 以下である可能性は低いです)。 この問題に対する1つの解決策は Accumulated Local Effect plots や short ALE plots で、これらは周辺分布の代わりに条件付き分布を使用します。
PDP は平均的な周辺効果のみを示すので 不均一な影響が隠れてしまう可能性があります。 半分のデータ点が予測と正の相関 -- 特徴量が大くなるほど予測結果も大きくなる -- 、もう半分のデータ点が負の相関 -- 特徴量が小さくなるほど予測結果は大きくなる -- を持つ特徴量を考えてみましょう。 このとき、PDP の曲線は水平になるでしょう、なぜなら両方のデータセットが互いに影響を打ち消し合うからです。 そうすると、その特徴量は予測には影響を与えないと結論づけてしまうでしょう。 これに対する解決策として、集計された線の代わりに、individual conditional expectation curves をプロットすることで、不均一な影響も明らかにできます。
5.1.4 ソフトウェアと代替手法
PDP を実装した R のパッケージはたくさんあります。 例えば著者は iml パッケージを使っていますが、pdp や DALEX もあります。 Python では、partial dependence plots は scikit-learn に標準で実装されていますし PDPBox も使えます。
この本で紹介されている PDP の代替手法には ALE plots や ICE curves があります。