4.4 決定木

線形回帰とロジスティック回帰モデルは特徴量と結果が非線形の時や特徴量が相互作用する時に失敗します。この状況こそ決定木が輝く時です！木をベースにしたモデルは、特徴量を、あるカットオフ値に基づいて複数回データを分割していきます。この分岐を通して、データセットは異なる部分集合に分割され、それぞれのインスタンスはこのうちの1つに属します。最後の部分集合は終端ノード (terminal node) または葉 (leaf node) と呼ばれていて、中間の部分集合は内部ノード (internal node)、または、分岐ノード (split node)と呼ばれています。それぞれの葉で結果を予測するためには、ノードに含まれる学習データの結果の平均値が使用されます。決定木は、分類でも回帰でも使われています。

決定木を成長させるためのさまざまなアルゴリズムが知られています。これらのアルゴリズムでは、決定木の構造（例:ノードあたりの分岐数）、分岐を見つけるための指標、いつ分岐を止めるか、そしてどのようにして葉の中で簡単なモデルを予測するかが異なっています。 CART (Classification And Regression Trees) アルゴリズムは、おそらく決定木を構築するためのもっとも有名なアルゴリズムです。本章ではCARTに焦点をあてますが、他の木も同様に解釈可能です。 CARTに関して、より詳細を知りたいのであれば、"The Elements of Statistical Learning" (Friedman, Hastie and Tibshirani 2009)¹⁷ の本をおすすめします。

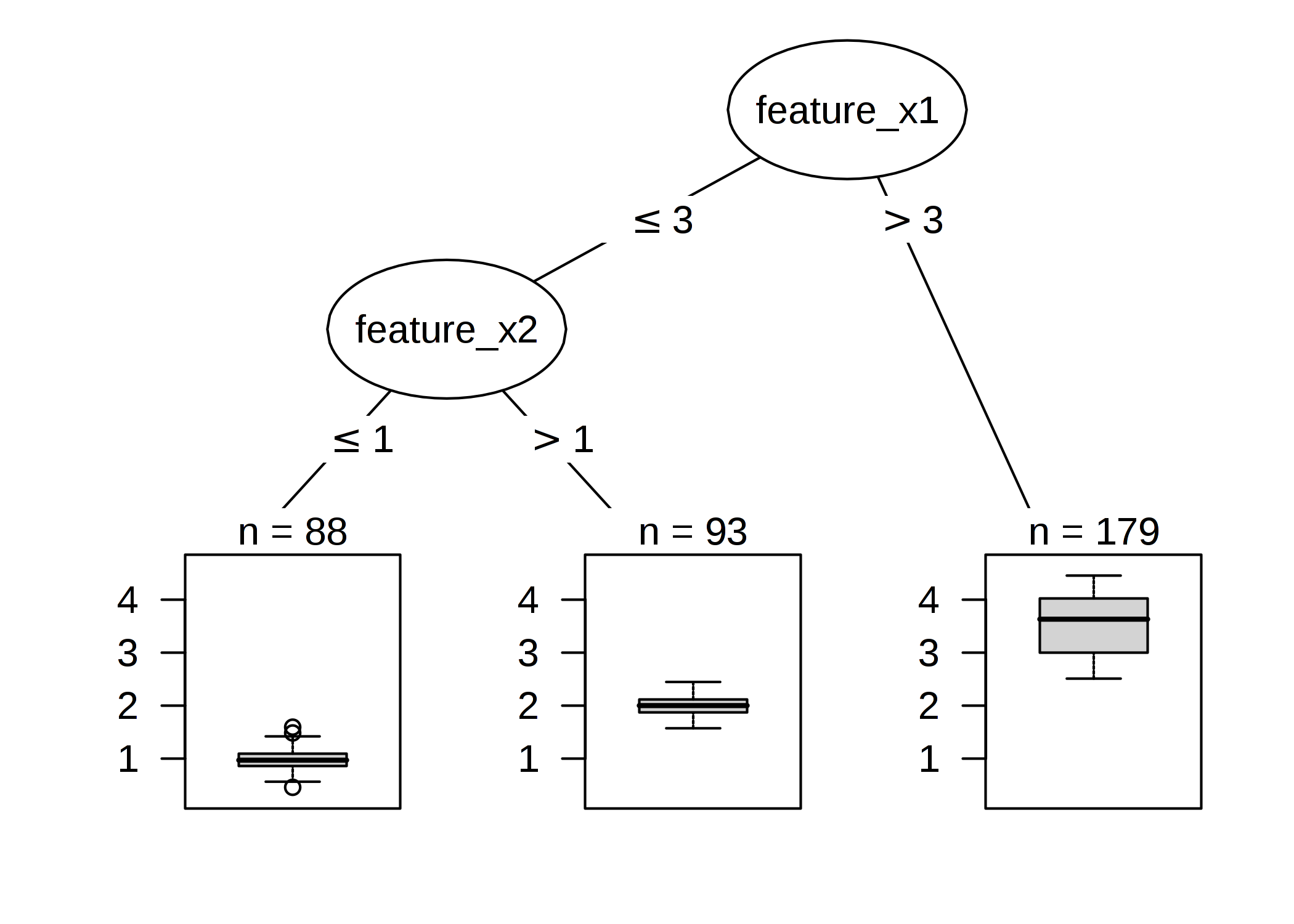
FIGURE 4.16: 人工データに対する決定木。特徴量 x1 が 3 より大きいとき、ノード 5 に割り当てられる。それ以外のインスタンスは特徴量 x2 が 1 を超えるかどうかでのノード 3 かノード 4 に割り当てられる。

下記の方程式は特徴量 x と結果 y の関係を記述しています。

\[\hat{y}=\hat{f}(x)=\sum_{m=1}^Mc_m{}I\{x\in{}R_m\}\]

それぞれのインスタンスは1つの葉　(=　部分集合 \(R_m\))　と対応します。 \(I_{\{x\in{}R_m\}}\) は、\(x\) が部分集合 \(R_m\) に属していれば 1 を、そうでないなら 0 を返す指示関数です。もし、インスタンスが葉 \(R_l\) に対応したとすると、予測による結果は \(\hat{y}=c_l\) となります。ただし、\(c_l\) は葉 \(R_l\) に対応する全ての学習データのインスタンスの平均値です。

しかし、これらの部分集合はどこからきたのでしょうか？これはとても簡単です: CARTは回帰であれば y の分散を、分類であれば y のクラス分布のジニ係数を最小にするように、特徴量を選び、カットオフ点を決定します。分散はノード内の y の値が平均からどの程度広がっているかを教えてくれます。ジニ係数はノードがどれだけ不純かを教えてくれます。例えば、ノード内に全てのクラスが同じ数あるとき、ノードは不純になります。一方で、ノードのクラスが1つだけの場合、純度が最大になります。ノードの中のデータ点がとても似た y の値を持つとき、分散やジニ係数は小さくなります。

結果として、最適なカットオフ点は、目標値に関して、2つの結果の部分集合ができるかぎり異なる値となるように選ばれます。カテゴリカル特徴量に対して、アルゴリズムは各カテゴリごとにまとめる様にして部分集合を作成します。特徴量ごとの最適なカットオフが決まったあと、アルゴリズムは、その中から分散やジニ係数に関して最適な分岐を与える特徴量を選び、この分岐を木に追加します。アルゴリズムは、両方の新しいノードに対して、この探索と分岐を停止の基準に到達するまで再帰的に繰り返します。考えられる停止基準は、分岐の前にノードの中に存在するべき最小のインスタンス数や、終端ノードに含まれるインスタンスの最小の数などがあります。

4.4.1 決定木の解釈

決定木の解釈は単純です:
根のノードから始めて、辺を辿って次のノードへと移っていきます。葉に到達すると、そのノードから予測結果を得ることができます。すべての枝は 'AND' で繋がっています。

例として、特徴量 x が閾値 c より[小さい/大きい] かつ ... のようになります。そして、予測結果は対応するノードに含まれるインスタンスの y の平均値になります。

特徴量重要度 (Feature importance)

決定木での特徴量の全体の重要度は次のように計算されます。その特徴量が使われた全ての分岐を見て、それが親のノードに比べてどのくらい分散やジニ係数を減少させているかを計算します。全部の重要度の和を100にスケーリングします。これはそれぞれの重要度がモデル全体の重要度に対する寄与率として解釈できることを意味しています。

木の分解

決定木の個々の予測は決定経路を特徴量ごとに1つの要素に分解することで説明可能です。木に沿って決定を追うことができ、それぞれの決定ノードに与えられた寄与度によって予測を説明できます。

根のノードは始点となります。根のノードを最終的な予測のために使うのであれば、単に学習データ全ての結果の平均を出力することになります。次の分岐では、経路上の次のノードによって、この和に項を減らしたり加えたりします。最終的な結果を得るためには、説明したいデータの経路に従って、式に加え続ける必要があります。

\[\hat{f}(x)=\bar{y}+\sum_{d=1}^D\text{split.contrib(d,x)}=\bar{y}+\sum_{j=1}^p\text{feat.contrib(j,x)}\]

個々のインスタンスの予測は、目的変数の平均に、根のノードからそのインスタンスの属する終端ノードの間で起こる D 回の分岐の全ての和を足したものになります。ただし、分岐の寄与度ではなく、特徴量の寄与度に関心があります。 1つの特徴量は、2回以上使われるかもしれませんし、1回も使われないかもしれません。 p 個の特徴量それぞれで、寄与度は加算でき、それぞれの特徴量がどれだけ予測に寄与してるかを解釈できます。

4.4.2 例

自転車レンタル数のデータをみてみましょう。決定木を用いて、ある日の自転車レンタル数を予測してみましょう。学習した決定木は以下の通りです。

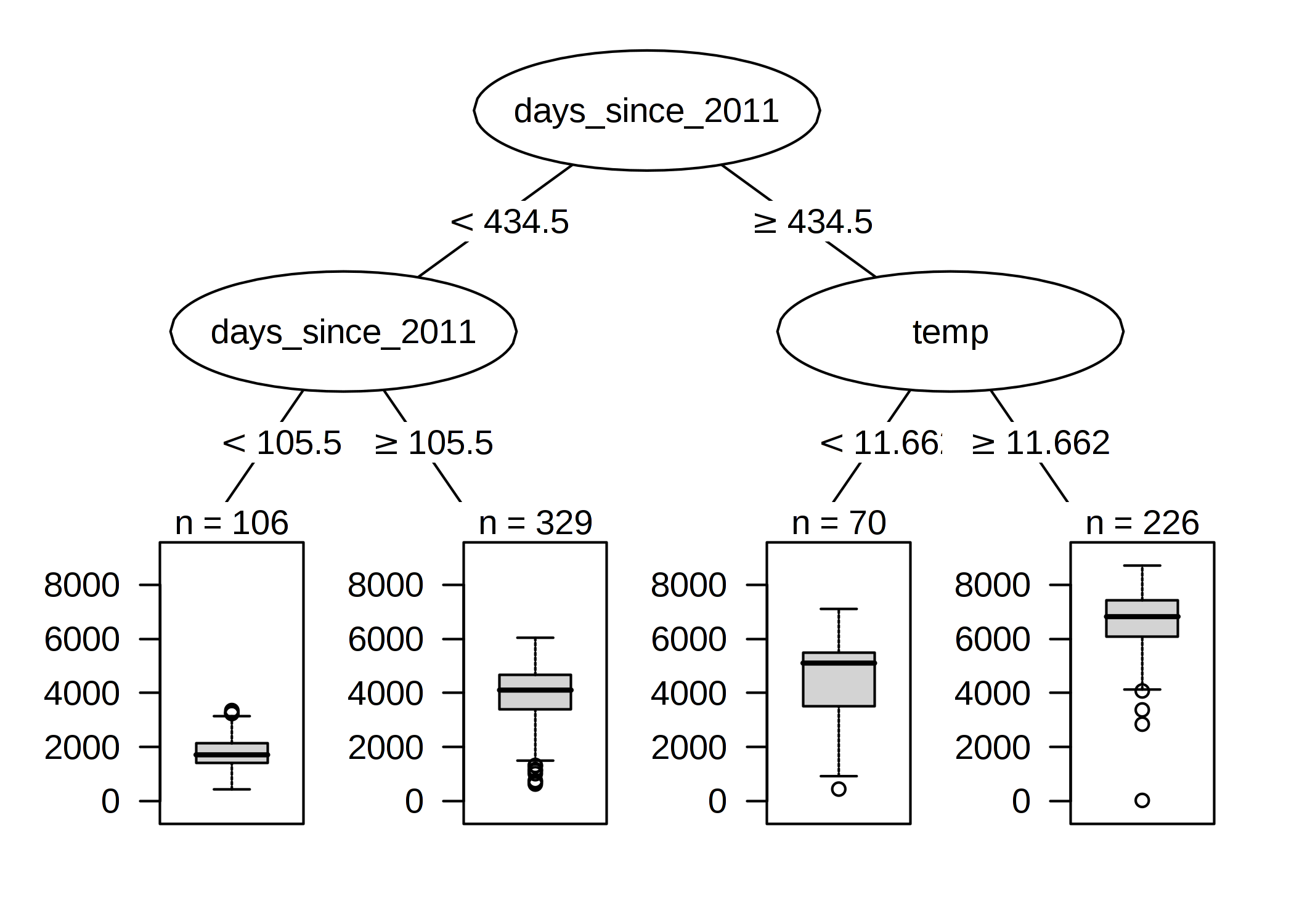
FIGURE 4.17: 自転車レンタル数のデータセットで学習された回帰木。木の最大深さは 2 に設定されている。トレンド特徴量 (2011年からの経過日数) と気温 (temp) が分割に選ばれている。箱ひげ図は終端ノードにおける自転車レンタル数の分布を示している。

1段目と2段目の1つの分岐は、時間のトレンドの特徴量によって行われていますが、データ収集を開始してからの日数を考慮に入れているので、レンタルサービスがだんだんと人気になっていった様子が表現されています。 105 日目より前のとき、自転車の数の予測は約 1800 台で、106 ~ 430 日目の間は約 3900 台となりました。430 日目以降については、予測は 4600 台 (気温が12度以下のとき)、または、6600 台 (気温が12度以上のとき) となりました。

特徴量重要度を見ると、ある特徴量がノードの純度をどの程度向上させるかが分かります。ここでは、自転車レンタル数の予測は回帰問題であるので、分散が使用されています。

可視化された決定木によって、温度と時間のトレンドの両方が分岐に使われていることはわかりますが、どの特徴量がどれほど重要かは定量化できていません。特徴量重要度は時間のトレンドが温度よりも需要であることを示しています。

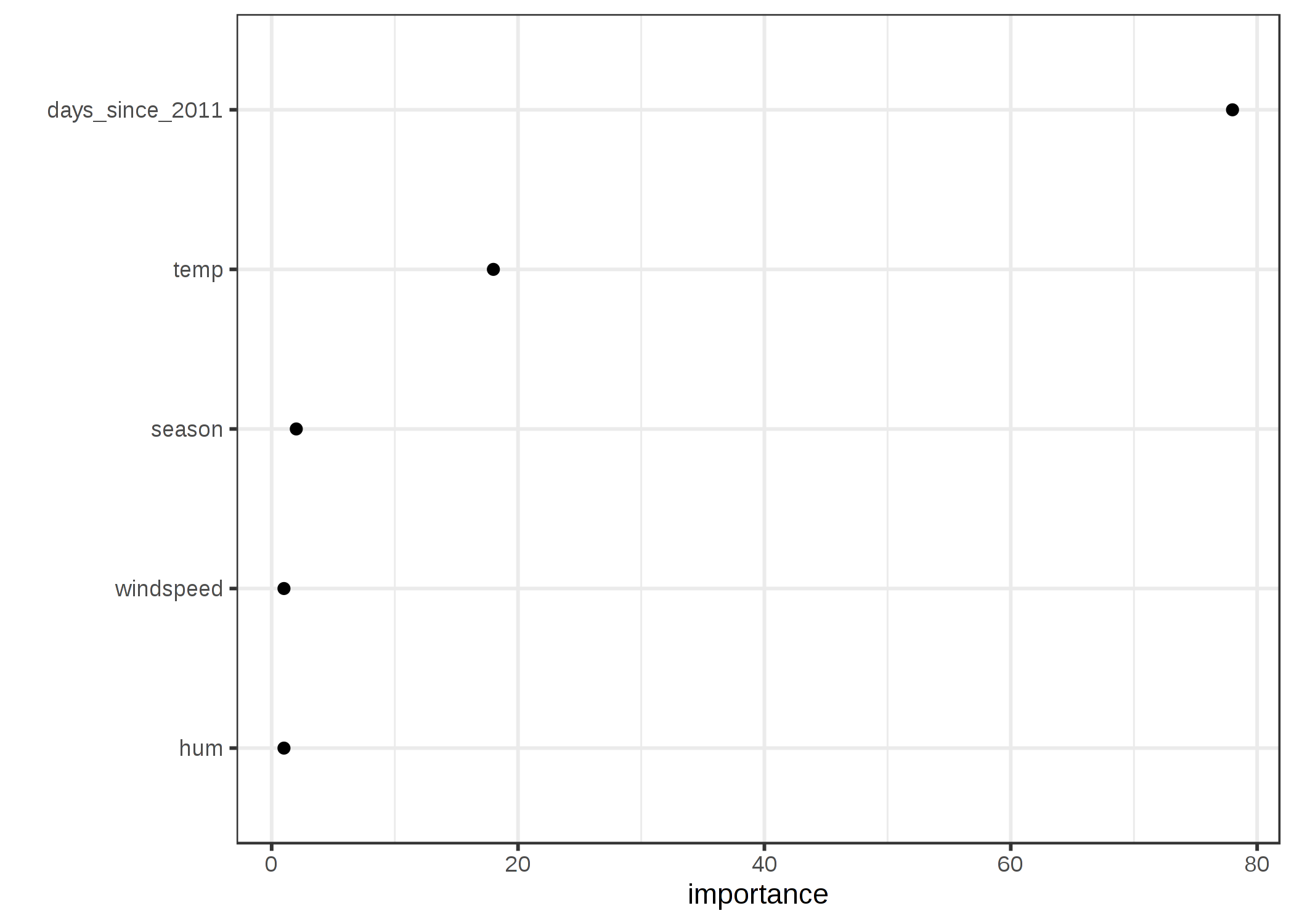
FIGURE 4.18: 平均的にノードの不純度がどの程度改善されたかによって計算された特徴量重要度

4.4.3 長所

決定木の構造は、データの特徴量間の相互作用を捉えるために理想的です。データは最終的に個別のグループに分かれるので、線型回帰のような多次元の超平面上の点として理解するよりも簡単です。決定木の構造は、ノードと辺により自然な描画が可能です。

決定木は"人間に優しい説明"の章で定義されているように、よい説明を与えることができます。決定木の構造は、自動的に個々のインスタンスに対して反事実的に予測値を考えるように誘導します。つまり、「この特徴量が分岐点より、大きい(小さい)なら、予測値は y2 ではなくて y1 であったのに。」というようになります。決定木の説明は対照的です。なぜなら、いつでも予測値と、決定木によって定められた"what if"シナリオ(他のノードの葉)と比べられるからです。もし、木の深さが1から3のように短かったら、最終的な説明は選択的です。深さが 3 の決定木は、個々のインスタンスの予測の説明を得るために、最大3つの特徴量と分岐点を必要とします。予測値の真実性は、決定木の予測性能に依存します。短い木の説明は非常に単純かつ一般的です。なぜなら、それぞれの分岐において、インスタンスは左右いずれかのノードに分かれていくので、このような二者択一は理解しやすいからです。

特徴量を変換する必要はありません。線形モデルでは、特徴量の対数をとる必要があるかもしれません。決定木は、特徴量の任意の単調変換に対して等価な振る舞いをします。

4.4.4 短所

決定木は線形な関係をうまく扱うことができません。任意の入力特徴量と結果の間の線形な関係は、分岐されて作られたステップ関数で近似されます。これは効率的ではありません。

これは、滑らかさの欠如と密接に関係しています。入力特徴量のわずかな変化が、予測結果に大きな影響を与える場合がありますが、これは望ましくありません。家のサイズを特徴量の1つとした決定木で住宅の価格を予測する場合を考えてみましょう。 100.5 平方メートルで分岐が発生したとします。この決定木の予測モデルを使ってユーザが家の価格を見積もるとどうなるでしょうか。家のサイズは 99 平方メートルだったとして、それを入力すると 200, 000 ユーロという予測結果を得ました。ユーザは 2 平方メートルの倉庫部屋の計算を忘れていたことに気がつきました。また、その倉庫には斜めの壁があったため、全ての面積を計算するべきか、半分にするべきか確証を持てませんでした。なので、100.0 平方メートルと 101.0 平方メートルの場合のどちらもを試すことに決めました。結果として、200, 000 ユーロと 205, 000 ユーロという予測結果が得られましたが、これはユーザの直感に反します。なぜなら、99 平方メートルが 100 平方メートルになっても価格に変化が生じなかったためです。

決定木は、かなり不安定でもあります。学習データがわずかに変わっただけで、全く異なった決定木が作られることがあります。これは、それぞれの分岐が親の分岐に依存しているためです。そのため、もし最初の分岐で異なる特徴量が選択されたとすると、全体の木構造に違いが生じます。このように、構造が容易に変化するため、モデルに信頼性があるとは言えません。

決定木は木の深さが小さいときは非常に解釈しやすいです。 終端ノードの数は深さにともなって急激に増加します。木の深さが深くなり、終端ノードの数が増加するにつれて、木の決定規則を理解することがより難しくなります。深さが 1 のときは2つの終端ノード、深さが 2 のときは最大4つ、深さが 3 のときは最大8つと、最大の終端ノードの数は、2の(木の深さ)乗となります。

4.4.5 ソフトウェア

この章の例では、CART (Classification And Regression Tree) の実装は rpart という R パッケージを用いました。 CART はPythonをはじめ、多くのプログラミング言語で実装されています。間違いなく、CARTはかなり古く、使い古されたアルゴリズムであり、木を学習するためのいくつかの興味深い新しいアルゴリズムがあります。決定木に関するいくつかの R パッケージの概要は Machine Learning and Statistical Learning CRAN Task View の "Recursive Partitioning" の項目のところに書かれています。

Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. "The elements of statistical learning". www.web.stanford.edu/~hastie/ElemStatLearn/ (2009).↩