4.5 決定規則
決定規則は、条件(前提とも呼ばれる)と予測値からなる単純なIF-THEN文です。 例えば、 もし、今日雨が降っていて4月であるなら(条件)、明日雨が降るだろう(予測)というものです。 予測は、単一の決定規則、もしくは、いくつかの決定規則の組み合わせによって行われます。
決定規則は一般的な構造に従います。 もし、条件を満たしているなら、特定の予測がされます。 決定規則は、おそらく最も解釈しやすい予測モデルです。 IF-THEN 構造は意味的には、自然言語や私たちの考え方に似ています。 ただし、条件がわかりやすい特徴量から構成され、条件の長さは短く(少数のANDで結合されている場合)、規則の数が多すぎない必要があります。 プログラミングでは IF-THEN のルールで書くことはとても自然です。 機械学習の新しい点は、決定規則がアルゴリズムによって学習されることです。
家の価値 ('low', 'medium', 'high') を予測するための決定規則をアルゴリズムによって学習することを想像してください。 このモデルから学習できた1つの決定規則として、もし家が 100 平方メートル以上の広さがあり、庭付きならば、価値は高い。 より正確には、IF 'size>100 AND garden=1' THEN 'value=high' とかけます。
決定規則を分解してみましょう。
- 'size>100' は、IF部分の第一条件です。
- 'garden=1' は、IF部分の第二条件です。
- 2つの条件を 'AND' で合わせて新しい条件を作ります。2つの条件がともに真のときのみ、規則は適用されます。
- 予測結果(THEN部分)は 'value=high' です。
決定規則は条件の中で少なくとも1つの 'feature=value' のステートメントを使用しますが 'AND' で追加できる数に制限はありません。 例外は、明示的なIF部分を持たないデフォルト規則で、他の規則が適用されない場合に適用されますが、これについては後で 解説します。 決定規則の有用性は通常、サポート (Support) と 正答率 (Accuracy) の2つの数字で表されます。
サポート (Support, 規則の適用範囲)
規則の条件が適用されるインスタンスの割合をサポートと呼びます。 例えば、size=big AND location=good THEN value=high という家の価値を予測する規則を考えてみましょう。 1000 軒中 100 軒が大きく、立地が良い場合、この規則のサポートは 10% となります。 予測部分 (THEN部分) は、サポートの計算には必要ありません。
正答率 (Accuracy, 規則の確信度)
規則の正答率とは、規則の条件が適用されるインスタンスに対して、どの程度、正しいクラスと予測できるかを示す指標です。 例えば、size=big AND location=good THEN value=high という規則が適用される 100 軒の中で、value=high が 85 軒、value=medium が 14 軒、value=low が 1 軒であったとすると、この規則の正答率は 85% となります。
通常、正答率とサポートはトレードオフの関係にあります。 条件に新しい特徴量を追加することで正答率を上げることができますが、サポートは低下します。
家の価値を予測するための良い分類器を作成するためには、1つの規則だけではなく、10 から 20 の規則を学習する必要があるかもしれません。 その時、より複雑なものになり、以下のような問題にぶつかるかもしれません。
- 規則の重複:
家の価値を予測したい時に、2つ以上の条件が適用され、それらが矛盾した予測結果であったとき、どうすればいいのでしょうか? - 規則の未適用:
家の価値を予測したい時に、どの規則も適用されないとき、どうしたらいいのでしょうか?
複数の規則を組み合わせるとき、決定リスト(順序付き)、決定集合(順序無し)の2つの主な戦略があります。 両方の戦略は、規則の重複問題に対して、異なる解決策を提示します。
決定リストは決定規則に順序付けを用います。 あるインスタンスに対して、最初の規則が真であれば、予測に最初の規則を用います。 偽であるならば、次の規則に進み、その規則を適用するかどうか確かめ、これを繰り返します。 決定リストは、適用される最初の規則の予測のみを返すことで、規則の重複問題を解決します。
決定集合は、いくつかの規則が高い投票権を持っているかもしれないということを除いては、民主主義の原理に似ています。 集合の中では、規則が互いに排他的であるか、多数決のような重複を解決する戦略が存在し、個々の規則が正答率や他の評価指標によって重み付けされます。 ただし、複数の規則が適用されると、解釈性が損なわれる可能性があるため注意が必要です。
決定リストも決定集合も、あるインスタンスに対して、どの規則も適用されないという問題が起こり得ます。 これは、デフォルト規則 (default rule) を導入することによって解決できます。 デフォルト規則は、どの規則も適用されない場合に適用される規則のことです。 デフォルト規則の予測は、他の規則でカバーされていないデータ点の中で最も頻度の高いクラスとすることが多いです。 規則の集合やリストが、特徴量空間全体をカバーしているとき、網羅的と呼びます。 デフォルト規則を追加することで、決定集合や決定リストは自動的に網羅的になります。
データから規則を学習する方法はたくさん存在しますが、本書ではそれら全てをカバーしていません。 この章では、それらのうちの3つを紹介します。 これらのアルゴリズムは、規則を学習するための一般的な考え方を幅広くカバーするように選ばれたため、これら3つは非常に異なるアプローチとなっています。
- OneR は、単一の特徴量から規則を学習します。 OneR の特徴は、単純かつ理解しやすいことであり、ベンチマークとして用いられます。
- Sequential covering は、繰り返し規則を学習していき、新しい規則でカバーされるデータ点を削除するという一般的な手法です。 この手法は、多くの規則を学習するアルゴリズムで用いられています。
- Bayesian Rule Lists は、ベイズ統計を用いて、あらかじめ発見された頻出パターンを決定リストに結合します。 事前に発見されたパターンを使用することも、多くの規則を学習するアルゴリズムで使用されているアプローチです。
規則を学習するために単一の最も良い特徴量を選ぶという、最も単純なアプローチから始めましょう。
4.5.1 単一の特徴量による規則学習 (OneR)
Holte(1993)18によって提案された OneR アルゴリズムは、最も単純な規則を導出するアルゴリズムの1つです。 全ての特徴量から,OneR は興味のある出力について最も情報量をもつ特徴量を選び、その特徴量から決定規則を作成します。
"One Rule" の略である OneR という名前にもかかわらず,このアルゴリズムは1つより多くのルールを生成します。 実際には、選択された最良の特徴量の値ごとに1つの規則を作ります。 したがって、OneFeatureRules のほうがふさわしい名前かもしれません。
このアルゴリズムは単純かつ高速です。
- 適切な間隔 (intervals) を選ぶことで,連続的な特徴量を離散化
- 各特徴量に対して、次を実行
- 特徴量の値と (カテゴリカルな) 出力間でクロステーブルを作成
- 各特徴量の値ごとに、クロステーブルから読み取れる特定の特徴量を持つインスタンスの、最も頻度の高いクラスを予測するための規則を作成
- 特徴量に対して、規則の誤差の合計を計算
- 誤差の合計が最小となる特徴量を選択
OneR は、選択された特徴量の全ての値を使用するため、常にデータセットにおける全インスタンスをカバーします。 欠損値は、追加の特徴量の値として扱うか事前に代入されます。
OneR モデルは分割が1つしかない決定木です。 その分割は、CART のように二分木である必要はなく、ユニークな特徴量の値の数に依存します。
OneR によってどのように最も良い特徴量が選ばれているか、例を見てみましょう。 次の表は、家についての価格、ロケーション、サイズ、ペットの可否の情報を持つ人工的なデータセットを示しています。 家の価格を予測するための単純なモデルを学習してみましょう。
| location | size | pets | value |
|---|---|---|---|
| good | small | yes | high |
| good | big | no | high |
| good | big | no | high |
| bad | medium | no | medium |
| good | medium | only cats | medium |
| good | small | only cats | medium |
| bad | medium | yes | medium |
| bad | small | yes | low |
| bad | medium | yes | low |
| bad | small | no | low |
OneR は各特徴と出力との間のクロステーブルを生成します。
| value=low | value=medium | value=high | |
|---|---|---|---|
| location=bad | 3 | 2 | 0 |
| location=good | 0 | 2 | 3 |
| value=low | value=medium | value=high | |
|---|---|---|---|
| size=big | 0 | 0 | 2 |
| size=medium | 1 | 3 | 0 |
| size=small | 2 | 1 | 1 |
| value=low | value=medium | value=high | |
|---|---|---|---|
| pets=no | 1 | 1 | 2 |
| pets=only cats | 0 | 2 | 0 |
| pets=yes | 2 | 1 | 1 |
各特徴に対して、1行ごとにクロステーブルを見ていき、各特徴量の値が、ルールにおける IF部分 に相当します。
この特徴量を持つインスタンスの最も一般的なクラスが予測値、つまり、規則の THEN部分 に相当します。 例えば、サイズに対しては、small、medium、big の3つの規則が得られます。
各特徴量に対して,生成された規則の全ての誤差率 (誤差の総和) を計算します。 「ロケーション」の特徴量は、bad と good を取りうる特徴量です。
ロケーションが bad の家の最も出現頻度が高い価格は low ですが、low を予測値としたとき、2つの誤りが生じます。 なぜなら、ロケーションが bad かつ、価格が medium である家が2つ存在するからです。 ロケーションが good の家の予測値を high としても、ロケーションが good かつ価格が medium の家が 2 軒あるため、ここでも2つの誤りが生じます。
ロケーションを特徴量に用いると、その誤差は 4/10、大きさでは 3/10、ペットの可否では 4/10 です。 大きさを特徴量とすると、最も低い誤差を持った規則が生成できるため、これが最終的に OneR モデルに用いられます。
IF size=small THEN value=small
IF size=medium THEN value=medium
IF size=big THEN value=high
OneR は、多くのレベルをもつ特徴量が選ばれる傾向にあります。なぜなら、それらの特徴量を用いると簡単に過学習してしまうためです。 全ての特徴量がランダムな値をもち、目的値に対して有用な値を持たないようなノイズのみを含むデータセットを想定してください。
いくつかの特徴量は他の特徴量より多くのレベルを持っています。 そのような多くのレベルを持った特徴量は過学習が起きやすくなります。 ある特徴量がインスタンスごとに異なるレベルを持っていたとすると、学習データ全体を完全に予測できてしまいます。 この問題に対する解決策は、データを学習用 (training data) と評価用 (validation data)に分けて、学習用のデータを用いて規則を学習し、選ばれた特徴量の評価は評価用のデータを用いて行います。
複数の特徴量が同じ誤差となるときが、もう1つの問題となります。 OneR では、このような場合は、誤差が最小の最初の特徴量を選択する、もしくは、カイ2乗検定の p値 が最小の特徴量を選択するようにします。
例
OneR を実データに適用してみましょう。 OneR アルゴリズムを子宮頸がんの分類タスク に適用してみます。 全ての連続な入力の特徴を5分位に離散化したところ、以下のような規則が作成されました。
| Age | prediction |
|---|---|
| (12.9,27.2] | Healthy |
| (27.2,41.4] | Healthy |
| (41.4,55.6] | Healthy |
| (55.6,69.8] | Healthy |
| (69.8,84.1] | Healthy |
OneR によって年齢の特徴量が最良の特徴量として選択されました。 がんは滅多に起こらないため、各規則はデータ数の多いクラスとなります。 従って、予測されるラベルが常に Healthy となり、これはあまり役に立たない結果と言えます。
このように、不均衡データに対するラベルの予測で使用しても意味がありません。 Age の間隔と Cancer/Healthy の間のクロステーブルに、癌にかかった女性の割合を加味するとより有益です。
| # Cancer | # Healthy | P(Cancer) | |
|---|---|---|---|
| Age=(12.9,27.2] | 26 | 477 | 0.05 |
| Age=(27.2,41.4] | 25 | 290 | 0.08 |
| Age=(41.4,55.6] | 4 | 31 | 0.11 |
| Age=(55.6,69.8] | 0 | 1 | 0.00 |
| Age=(69.8,84.1] | 0 | 4 | 0.00 |
ただし、解釈を始める前に注意しなければいけないことがあります。 全ての特徴量の全ての値に対する予測は Healthy だったため、全ての特徴量に対する合計の誤差率は同じです。 複数の特徴量で合計の誤差率が等しい場合、基本的には、最も誤差率の低い特徴量の中で、最初のものが使用されます(全ての特徴量は誤差率 55/858)。これがたまたま「Age feature」だったのです。
OneR は回帰問題では使用できません。 しかし、出力をいくつかの区間に分割することで回帰問題を分類問題に落とし込むことができます。 この手法を自転車レンタル台数予測に使ってみましょう。 自転車の数を四分位数(0~25%, 25~50%, 50~75%, 75~100%)で分割することで、OneR を用いて予測します。 OneR モデルで選択された特徴量の表は以下の通りです。
| mnth | prediction |
|---|---|
| JAN | [22,3152] |
| FEB | [22,3152] |
| MAR | [22,3152] |
| APR | (3152,4548] |
| MAY | (5956,8714] |
| JUN | (4548,5956] |
| JUL | (5956,8714] |
| AUG | (5956,8714] |
| SEP | (5956,8714] |
| OKT | (5956,8714] |
| NOV | (3152,4548] |
| DEZ | [22,3152] |
選択された特徴量は月 (month) でした。 月の特徴量は(驚くべきことに!)12段階に分かれており、これは他のほとんどの特徴量よりも多いです。 そのため、過学習の危険性があります。 しかし、より楽観的な立場からすると、月の特徴量は季節のトレンド(例えば、冬はレンタル自転車の人気がなくなるなど)を捉えることができるため、その予測は賢明なのかもしれません。
それでは、単純な OneR アルゴリズムから、より複雑な手順で、いくつかの特徴量からなる複雑な条件を持つ規則を学習するための Sequential Covering に移りましょう。
4.5.2 Sequential Covering
Sequential Covering とは、1つの規則を繰り返し学習し、ルールごとにデータセット全体をカバーする決定リスト(または決定集合)を作成する一般的な手続きです。 多くの規則を学習するアルゴリズムは、Sequential Covering の一種です。 この章では、手法の概要を紹介し、例として、Sequential Covering の応用形である RIPPER を使用します。
アイデアはシンプルです。 まずはいくつかのデータに当てはまる良い規則を見つけます。 そして、その規則でカバーされる全てのデータ点を削除します。 データ点がカバーされるのは、条件が適用されたときであり、その点が正しく分類されたかどうかとは関係がないことに注意してください。 この規則を学習し、カバーされた点を削除することを、残りのデータ点がなくなるか、他の停止条件が満たされるまで繰り返します。 その結果、決定リストが得られます。 この、規則の学習とカバーされたデータ点の削除を繰り返す手法を 「separate-and-conquer」と呼びます。
データの一部をカバーする単一のルールを作成できるアルゴリズムをすでに我々は持っているとします。 2つのクラス(positiveとnegative)に対する、sequential covering アルゴリズムは 以下のように動作します。
- 空の規則のリストから始める(rlist)
- 規則 r を学習
- 規則のリストがある閾値を下回っている間(もしくは positive な例がまだカバーされていない間):
- 規則 r を rlist に追加
- 規則 r によってカバーされるデータ点を全て削除
- 残ったデータに対して、他の規則を学習
- 決定リストを返す
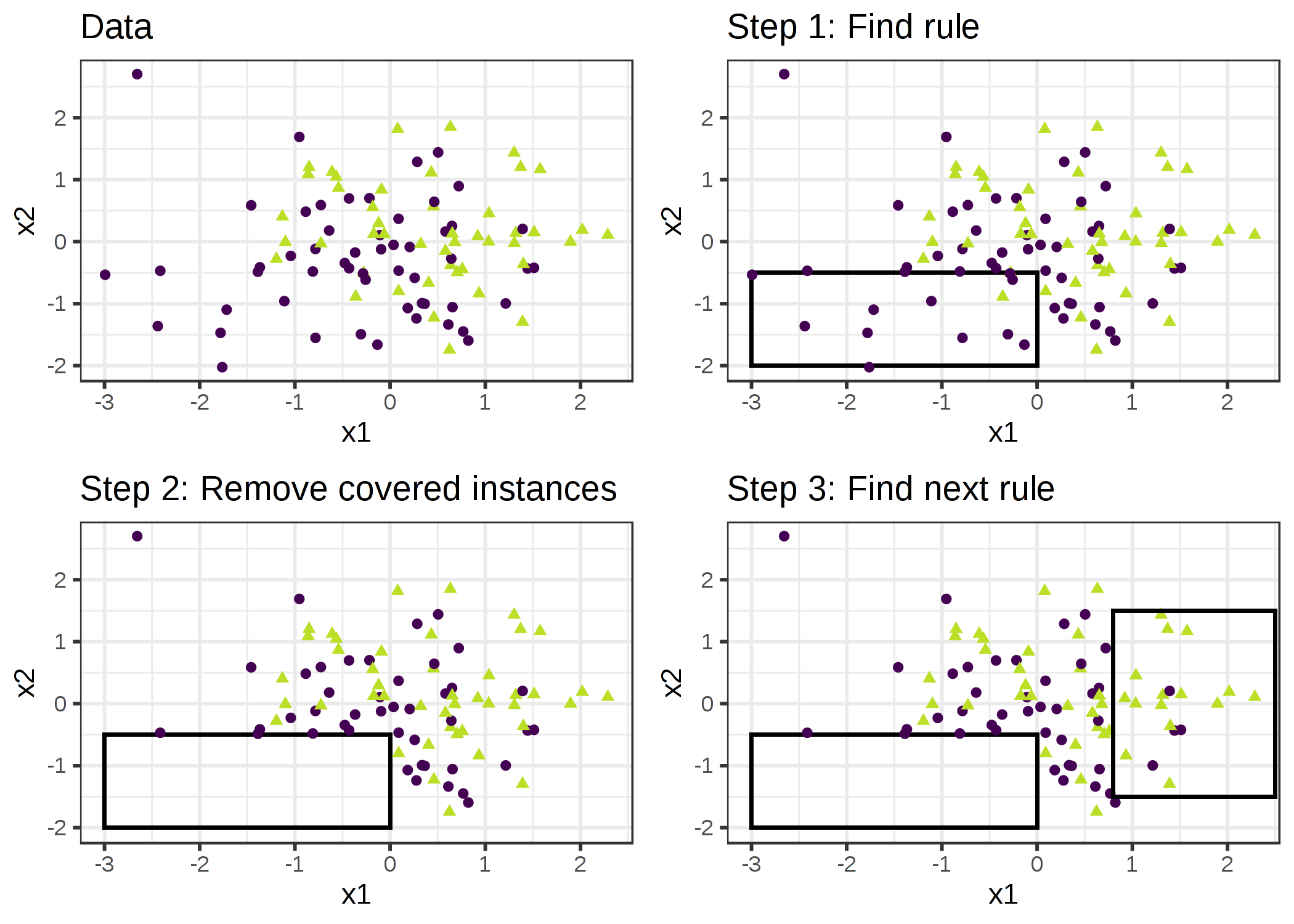
FIGURE 4.19: アルゴリズムは単一の規則で特徴空間を順次カバーし、それらのルールで既にカバーされているデータ点を削除していくことで動作します。可視化のために、特徴量 x1 と x2 は連続量ですが、ほとんどの規則学習アルゴリズムはカテゴリカル特徴量を必要とします。
例として、家のサイズ、ロケーション、およびペットの可否から家の価値を予測するタスクおよびデータセットがあるとします。 初めに学習する規則は、もし、size=big かつ location=good ならば、value=high となります。 そして、データセットから全てのよいロケーションにある大きな家を削除します。 残ったデータで、我々は次の規則を学習すると、location=good ならば、value=medium となります。 注意すべき点としては、この規則は、ロケーションがよく大きな家を除いたデータで学習されており、ロケーションのいい家は medium か small しか残されていないということです。
多クラスの設定の場合は、アプローチを変える必要があります。 初めに、クラスは普及率を昇順に並べます。 sequential covering アルゴリズムは、最も一般的でないクラスから始まり、それのための規則を学習し、カバーされたインスタンスを全て削除し、次に一般的でないクラスに移動していきます。 現在のクラスは常にポジティブクラスとして扱われ、より高い普及率を持つ全てのクラスはネガティブクラスとしてまとめられます。 最後のクラスはデフォルト規則となります。 これは分類問題における one-versus-all 戦略とも呼ばれます。
どうやって1つのルールを学習するのでしょうか。 OneR アルゴリズムは、全ての特徴空間をカバーするので、役に立たないでしょう。 しかし、他にも多くのいろいろな可能性があります。 1つの可能性としては、ビームサーチを用いて決定木から単一の規則を学習することです。
- 決定木を(CARTや他の木学習アルゴリズムを用いて)学習します。
- ルートノードから出発し、再帰的に最も不純度の低いノード(例:誤分類率が最も低いノード)を選択していきます。
- 規則の予測には、終端ノードにおける多数派のクラスが使用されます。つまり、そのノードに到達までのパスがルールの条件として使われます。
以下の図は、木をビームサーチした様子です。
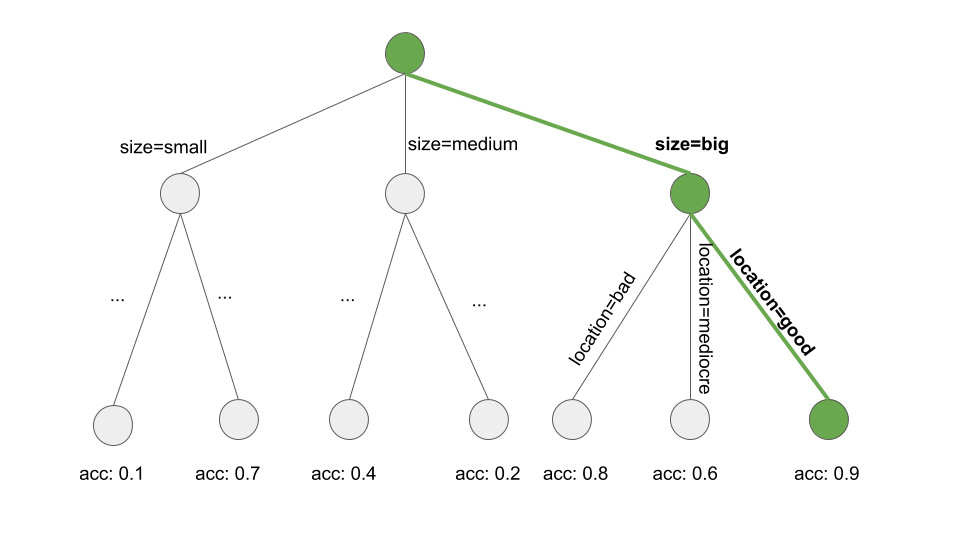
FIGURE 4.20: 決定木のパスを探索することで規則を学習する。決定木は興味のある目的値を予測するために成長する。ルートノードから出発し、純度の高い(例: 正答率の高い)部分集合のパスへ貪欲的に遷移し、全ての分割の値を規則の条件に加える。最終的に、もし、location=good かつ size=big ならば value=highを得る。
単一の規則を学習することは、全ての可能な規則からなる空間が探索空間であるような探索問題です。 探索のゴールは、何らかの基準によって最適な規則を見つけることです。 いくつかの異なる探索の方策があります。 山登り法 (hill-climbing)、ビームサーチ (beam search)、全探索 (exhaustive search)、最良優先探索 (best-first search)、順序探索 (ordered search), 確率的探索 (stochastic search), トップダウン探索 (top-down search)、ボトムアップ探索 (bottom-up search)、など。
Cohen (1995)19 による RIPPER (Repeated Incremental Pruning to Produce Error Reduction) は Sequential Covering アルゴリズムの一種です。 RIPPER はより洗練されており、後処理 (rule pruning) を使って決定リスト (または、決定集合)を最適化します。 RIPPER は順序付き、順序なしモードで実行することができ、決定リストまたは決定集合のいずれかを生成できます。
例
例として、RIPPER を使用してみましょう。
RIPPER アルゴリズムは、子宮頸癌の分類問題において、規則を発見しません。
RIPPER を自転車レンタル台数の予測の回帰問題に適用したとき、いくつかの規則が見つかります。 RIPPER は分類問題に対して動作するため、自転車の数はカテゴリカルな出力に変換しなければいけません。 そのため、自転車の数は四分位数に変換しています。 例えば、(4548, 5956) は予測された自転車の数が 4548 台から 5956 台の間の区間を示しています。 次の表は、学習された規則の決定リストを示しています。
| rules |
|---|
| (days_since_2011 >= 438) and (temp >= 17) and (temp <= 27) and (hum <= 67) => cnt=(5956,8714] |
| (days_since_2011 >= 443) and (temp >= 12) and (weathersit = GOOD) and (hum >= 59) => cnt=(5956,8714] |
| (days_since_2011 >= 441) and (windspeed <= 10) and (temp >= 13) => cnt=(5956,8714] |
| (temp >= 12) and (hum <= 68) and (days_since_2011 >= 551) => cnt=(5956,8714] |
| (days_since_2011 >= 100) and (days_since_2011 <= 434) and (hum <= 72) and (workingday = WORKING DAY) => cnt=(3152,4548] |
| (days_since_2011 >= 106) and (days_since_2011 <= 323) => cnt=(3152,4548] |
| => cnt=[22,3152] |
解釈は単純明快です。 もし、条件が適用されたら、右側の区間の自転車の台数であると予測します。 最後の規則はデフォルト規則で、インスタンスに対してどの規則も適用されなかったときに適用されます。 新しいインスタンスに対して予測するためには、リストの上から出発し、規則が適用されるかチェックします。 条件がマッチしたとき、規則の右側の値がこのインスタンスに対する予測となります。 デフォルト規則は、常に予測値が存在することを保証します。
4.5.3 Bayesian Rule Lists
この章では、次の大まかな手順に従って、決定リストを学習する別のアプローチを紹介します。
- 決定規則の条件として使える頻出パターンをデータから事前にマイニングしておきます。
- マイニングされた規則からいくつかを選択し、決定リストを学習します。
このようなアプローチを Bayesian Rule Lists (Lethan et. al, 2015)20または、略して BRL と呼びます。 BRL はベイズ統計を用いて、FP-tree アルゴリズム (Borgelt 2005)21 でマイニングされた頻出パターンから決定リストを学習しますが、まずは BRL の最初のステップからゆっくり始めましょう。
頻出パターンの事前マイニング
頻出パターンとは、特徴量の頻繁な共起のことを言います。 BRL アルゴリズムの前処理ステップとして、特徴量を使って頻出パターンを抽出します(この段階では目的値は不必要です)。 パターンには、size=medium のような単一の特徴量のものや、size=medium AND location=bad のような特徴量の組み合わせのものがあります。
パターンの頻度は次のように、データセット内のサポートで定量化されます。
\[Support(x_j=A)=\frac{1}n{}\sum_{i=1}^nI(x^{(i)}_{j}=A)\]
ただし、A は特徴量の値、n はデータセット内のデータの数、I はデータ i の特徴 \(x_j\) のレベルが A の場合は 1、そうでない場合は 0 を返す指示関数です。 家の価値のデータセットで、もし家の20%にベランダがなく、80%で一個以上のベランダがあった場合、パターン balcony=0 に対するサポートは20%になります。 サポートは、balcony=0 AND pets=allowed のような、特徴量の組み合わせについても同様に測定できます。
AprioriやFP-Growth のような、頻出パターンを発見するためのアルゴリズムはたくさんあります。 結果のパターンは常に同じなので、計算速度だけが異なるため、どれを用いるかはそれほど重要ではありません。
Aprioriアルゴリズムがどのように頻繁なパターンを見つけるかについて大まかに説明します。 実は、Aprioriアルゴリズムは2つの部分で構成されており、まず最初に頻出パターンを見つけ、その次に、それらから相関規則を構築します。 BRL アルゴリズムにおいては、Aprioriアルゴリズムの最初の部分で生成される頻出パターンにのみ関心があります。
最初のステップでは、ユーザが定義した閾値より大きいサポートを持つすべての特徴量から始まります。 ユーザが最小のサポートを10%に設定しており、家の5%のみが size=big になっている場合、その特徴量の値は削除され、 size=medium と size=small のみがパターンとして保持されます。 これは、 size=big を持つ家がデータから削除されるということではなく、 size=big が頻出パターンとして返されなくなるという意味です。 Aprioriアルゴリズムは、単一の特徴量を持つ頻出パターンに基づいて、より高次の特徴量の組み合わせを繰り返し発見します。 パターンは、 feature=value ステートメントを論理 AND と組み合わせて構築されます。(例: size=medium AND location=bad ) 生成されたパターンのうち、閾値未満のサポートを持つものは削除されます。 最後には、すべての頻繁なパターンを持つことになります。 頻出パターンの部分集合もまた、頻出パターンになります。これはApriori propertyと呼ばれます。 これは、直感的にも成り立ちます。 パターンからある条件を外すと、削減された後のパターンは、より広い(または同じ)範囲のデータをカバーできるようになり、範囲が狭くなることはありえません。 例えば、家の20%が size=medium AND location=good ならば、 size=medium のみの家のサポートは20%以上になります。 このApriori propertyは、検査すべきパターンの数を減らすために使われます。 頻出パターンに対してのみ、高次のパターンをチェックする必要があります。
これで BRL アルゴリズムのための条件の事前マイニングが完了しました。 BRL の次のステップに進む前に、パターンの事前マイニングに基づく規則学習の別の方法を紹介します。 他のアプローチでは、関心のある出力結果を頻出パターンのマイニングプロセスに含め、Apriori アルゴリズムの2番目のステップである IF-THEN ルールを構築する部分でも使用することが提案されています。 教師なし学習アルゴリズムなので、THEN 部分に関心のない特徴量も含まれてしまいます。 ただし、THEN 部分に関心のある出力結果のみを持つ規則でフィルタリングできます。 これらの規則はすでに決定集合を形成していますが、規則の再配列、削除、再結合もできます。
しかしながら、BRL アルゴリズムでは、ベイズ統計を用いて頻出パターンから THEN 部分と決定リストに配置する方法を学習します。
Bayesian Rule Lists による学習
BRL アルゴリズムのゴールは、事前にマイニングされた条件から選択して、なるべく少ない規則、短い条件のリストとなることを優先させながら、正確な決定リストを学習することです。 BRL は、条件の長さ(短いルールで)と規則の数(短いリストで)に関する事前分布を用いて決定リストの分布を定義することにより、この目標を達成します。
リストの事後確率分布により、短さの仮定とどの程度データに適合しているかに基づいて、決定リストがどの程度尤もらしいかを言うことができます。 私たちの目標は、この事後確率を最大化するリストを見つけることです。 リストの分布から直接、最良のリストを見つけることはできないため、BRL は次のような手順に従います。
- 事前分布からランダムに最初の決定リストを生成します。
- 規則の追加、切り替え、または削除を繰り返し行い、結果のリストが、リストの事後分布に従うようにします。
- 事後分布に従ってサンプリングされたリストから最も確率の高い決定リストを選択します。
アルゴリズムをさらに詳しく見ていきましょう。 このアルゴリズムは、FP-Growth アルゴリズムを用いた特徴量のパターンを事前マイニングすることから始まります。 BRL は目的値の分布と、目的値の分布を定義するパラメータの分布について、いくつかの仮定をします。 (これがベイズ統計です。) ベイズ統計に慣れていない方は、以下の説明にとらわれすぎないようにしてください。 ベイズ統計のアプローチは、モデルをデータにフィットさせる一方で、既存の知識や必要条件(いわゆる事前分布)を組み合わせる方法であることを知っておくことが重要です。 決定リストの場合、決定リストの規則が短くなるように事前分布によって調整されるため、ベイズ統計のアプローチは理にかなっています。
ゴールは、事後分布から決定リスト d をサンプリングすることです。
\[\underbrace{p(d|x,y,A,\alpha,\lambda,\eta)}_{posteriori}\propto\underbrace{p(y|x,d,\alpha)}_{likelihood}\cdot\underbrace{p(d|A,\lambda,\eta)}_{priori}\]
ただし、d は決定リスト、x は特徴量、y は目的値、A は事前にマイニングされた条件の集合、\(\lambda\) は事前に予想される決定リストの長さ、\(\eta\) は事前に予想される規則の中の条件の数、\(\alpha\) は正と負クラスに対する事前の擬似的なカウントで、 (1,1) に固定する方が良いです。
\[p(d|x,y,A,\alpha,\lambda,\eta)\]
この式は観測されたデータと事前の仮定に基づいて、決定リストの可能性を定量化します。 これは、決定リストとデータが与えられたときの出力 y の尤度と、与えられた事前情報と事前にマイニングされた条件に対するリストの確率をかけたものに比例します。
\[p(y|x,d,\alpha)\]
この式は、決定リストとデータが与えられたときに観測された y の尤度です。 BRL では y はディリクレ多項分布 (Dirichlet-Multinomial distribution) によって生成されることを仮定しています。 決定リスト d がデータをうまく説明できるほど、尤度は高くなります。
\[p(d|A,\lambda,\eta)\]
この式は、決定リストの事前分布です。 これは、リスト内の規則の数に対するパラメータ \(\lambda\) の truncated Poisson distribution と 規則の条件の特徴量の値の数に対するパラメータ \(\eta\) の truncated Poisson distribution を掛け合わせます。 決定リストは、出力 y をうまく説明し、事前の仮定に従っている可能性が高いほど、事後確率が高くなります。
ベイズ統計の推定には少しトリッキーです。なぜなら、直接正解を計算できるとは限らず、通常は、候補を選んで評価し、マルコフ連鎖モンテカルロ法 (MCMC) を用いて事後推定を更新する必要があるからです。 決定リストの場合、決定リストの分布から引き出す必要があるため、さらに複雑になります。
BRL の著者は、まず最初の決定リストを作成し、次にそれを繰り返し変更して、リストの事後分布(決定リストのマルコフ連鎖)から決定リストのサンプルを生成することを提案しています。 これによって得られる結果は最初の決定リストに依存する、この手順を繰り返し実行し、多様なリストを確保することが望ましいです。ソフトウェアの実装の中では、基本的に10回繰り返します。
以下の手順は、最初の決定リストの作り方を示しています。
- FP-Growthでパターンを事前にマイニング
- truncated Poisson distribution から、リストの長さのパラメータ m をサンプリング
- デフォルト規則の場合 (他に何も適用しない場合に用いられるルール)は以下を実行
- 目的値に関するディリクレ多項分布のパラメータ \(\theta_0\) をサンプリング
- 決定リストの規則 j = 1,...,m に対して、以下を実行
- 規則 j に対して、規則の長さのパラメータ l (条件の数) をサンプリング
- 事前にマイニングした条件から、長さが \(l_j\) の条件をサンプリング
- THEN部分(規則によって与えられた出力結果の分布)に対して、ディリクレ多項分布のパラメータをサンプリング
- データセットのそれぞれの観測値に対して以下を実行
- 決定リストを上から下に探索し、最初に適用する規則を見つける
- 適合するルールによって提案された確率分布 (二項分布) から予測結果を引き出す
次のステップは、決定リストの事後分布から多くのサンプルを取得するために、この最初のサンプルからスタートし、たくさんの新しいリストを生成することです。
新しい決定リストは最初のリストから開始し、規則をリスト内の別の場所に移動するか、事前にマイニングされた条件から現在の決定リストに規則を追加するか、もしくは決定リストから規則を削除することによってサンプリングされます。 これらの規則の切り替え、追加、削除は無作為に選ばれて適用されます。 それぞれのステップにおいて、アルゴリズムは決定リストの(正答率と短さの組み合わさった)事後確率を評価します。 Metropolis Hastings アルゴリズムは、事後確率が高い決定リストをサンプリングすることを保証します。 この手順によって、決定リストの分布から多くのサンプルを得ることができます。 BRL アルゴリズムは最も高い事後確率を持つサンプルの決定リストを選択します。
例
理論はこれぐらいにして、BRL 法の動作を見てみましょう。 例では、Yang らによる BRL をより高速化した Scalable Bayesian Rule List (SBRL, 2017) 22を使用します。 SBRL アルゴリズムを子宮頸がんのリスクの予測に適用します。 まずはじめに、全ての入力特徴量を SBRL アルゴリズムで使用可能なように離散化する必要があります。 この目的のために、連続特徴量は分位数の頻度に基づいてビン化しています。 すると、以下のようなルールを得ることができます。
| rules |
|---|
| If {STDs=1} (rule[259]) then positive probability = 0.16049383 |
| else if {Hormonal.Contraceptives..years.=[0,10)} (rule[82]) then positive probability = 0.04685408 |
| else (default rule) then positive probability = 0.27777778 |
予測の THEN 部分がクラスの結果ではなく、がんの予測確率であるため、実用的なルールを得ることができていることに注意してください。
条件は、あらかじめ探索された FP-Growth アルゴリズムを使って得られたパターンから選択されました。 次の表は、SBRL アルゴリズムが決定リストを作成するために選択できる条件の候補を示しています。 ユーザが設定した、条件に含まれる最大の特徴量の数は 2 としています。 以下が 10 パターンの例です。
| pre-mined conditions |
|---|
| Num.of.pregnancies=[3.67,7.33) |
| IUD=0,STDs=1 |
| Number.of.sexual.partners=[1,10),STDs..Time.since.last.diagnosis=[1,8) |
| First.sexual.intercourse=[10,17.3),STDs=0 |
| Smokes=1,IUD..years.=[0,6.33) |
| Hormonal.Contraceptives..years.=[10,20),STDs..Number.of.diagnosis=[0,1) |
| Age=[13,36.7) |
| Hormonal.Contraceptives=1,STDs..Number.of.diagnosis=[0,1) |
| Number.of.sexual.partners=[1,10),STDs..number.=[0,1.33) |
| STDs..number.=[1.33,2.67),STDs..Time.since.first.diagnosis=[1,8) |
次に、自転車レンタル予測のタスクにも、SBRL アルゴリズムを適用してみましょう。 これは、自転車の数を予測する問題が、二値分類の問題に変換できたときのみ使用可能です。 そのため、ここでは恣意的に 1 日の自転車レンタル数が 4000 を超えるとき 1 , そうでないときは0とラベルを付与することで、分類問題に変換しています。
| rules |
|---|
| If {yr=2011,temp=[-5.22,7.35)} (rule[718]) then positive probability = 0.01041667 |
| else if {yr=2012,temp=[7.35,19.9)} (rule[823]) then positive probability = 0.88125000 |
| else if {yr=2012,temp=[19.9,32.5]} (rule[816]) then positive probability = 0.99253731 |
| else if {season=SPRING} (rule[351]) then positive probability = 0.06410256 |
| else if {temp=[7.35,19.9)} (rule[489]) then positive probability = 0.44444444 |
| else (default rule) then positive probability = 0.79746835 |
気温が摂氏 17 度で、2012 年の 1日で自転車の数が 4000 を超える確率を予測してみましょう。 最初のルールは、2011 年の時のみ適用されるため、今回は適用されません。 2012 年で 17 度のときは、区間 [7.35,19.9) に入っているので、 2つ目のルールは適用されます。 予測の結果、4000 台を超える確率は 88% となりました。
4.5.4 長所
この章では一般的な IF-THEN ルールの長所について議論します。
IF-THEN ルールは解釈することが簡単です。 これはおそらく最も解釈しやすい解釈可能モデルと言えます。 ただし、このように言えるのは、ルールの数が少ないときに限られ、ある規則の条件が少なく(多くとも3が好ましい)、規則が決定リストか重複のない決定集合で管理される場合です。
決定規則は決定木のように表現力がありながら、よりコンパクトです。 決定木は複製された部分技に苦しむことが多く、これは、分岐点の左右の子ノードが同じ構造を持つときに起こります。
どのルールに決めるのかの少数のバイナリステートメントを確認するだけなので、IF-THEN ルールの予測は高速です。
決定規則は、入力特徴量の単調変換に対しては、条件に関する閾値が変わるだけなので、頑健です。 条件が適用されるかどうかの問題なので、外れ値に対しても頑健です。
IF-THEN ルールは通常、少数な特徴量だけを含むスパースなモデルを生成します。 モデルに関連する特徴量だけを選択するのです。 例えば、線形モデルは基本的にはすべての入力特徴量に重みを割り当てます。 無関係な特徴量は IF-THEN ルールでは、単に無視されるでしょう。
OneR のような単純な規則は、より複雑なアルゴリズムに対するベースラインとして使えるでしょう。
4.5.5 短所
この章では一般的な IF-THEN ルールの欠点について扱います。
IF-THEN ルールに関する研究や書物では分類に焦点を当ていて、完全に回帰を無視しています。 ほとんどの場合、連続値をある区間に分割することで分類問題に変形できますが、それによって必ず情報を失います。 一般的に、回帰と分類の両方に使える方法はより魅力的です。
また、特徴量はカテゴリカルでなければいけません。 つまり、量的特徴量を使いたいときは、カテゴリカル化しなければいけません。 連続値の特徴量をある区間に切る方法は沢山ありますが、これは自明なことではなく、明確な答えのない多くの疑問が付随します。 いくつの区間で特徴量を分けるべきか、分割の基準はなにか、固定長の区間か、分位点か、その他のなにかか。 連続値の特徴量をカテゴリカル化するのは重大な問題であるのに、無視されがちで、多くの人はここで例示したように、単に次の最も良い方法を使います。
多くの古いルール学習アルゴリズムは過学習する傾向があります。 ここで紹介したすべてのアルゴリズムは、過学習を防ぐために少なくともいくつかの安全策を講じています。 OneR は1つの特徴量しか使わないように制限されており (ただし、特徴量が多すぎるレベルを持っていたり、多重検定問題に相当するような特徴量が多すぎる場合には問題になります)、RIPPER ではプルーニングを行い、Bayesian Rule Lists では決定リストの事前分布として制約を課しています。
決定規則は、特徴量と出力との線形な関係を表現することには向いていません。 これは、決定木と共通する問題です。 決定木や決定規則はステップ状の予測関数しか生成できないため、常に予測の変化は離散的な階段状となり滑らかなカーブにはなりません。 これは、入力がカテゴリカルでなければいけないことに関連した問題です。 決定木では、分割によって暗黙的にカテゴリカル化が行われています。
4.5.6 ソフトウェアと代替手法
OneR は R パッケージ OneRに実装されており、この本の例でも使用されています。 OneR は機械学習ライブラリのWekaにも実装されており、Java や R 、そしてPythonで利用できます。 RIPPER も Weka で実装されています。例えば、私は RWekaパッケージ内の JRIP の R 実装を使いました。 SBRL も、この本の例で実行しているように、Rパッケージで利用できます。 他にも、Python や C言語 でも使えます。
決定集合や決定リストを学習する方法の全ての代替手法をリスト化することはしていませんが、ここでは、それらの要約を紹介します。 Fuernkranz らによる "Foundations of Rule Learning" (2012)23 の 本をおすすめします。 これは、決定規則に関して、より深い知識を身に付けたい人にとって役立つでしょう。 この本では、学習規則を考えるための全体的なフレームワークや、多くの規則を学習させるアルゴリズムを紹介しています。 また、こちらの資料(Weka rule learners) もおすすめで、RIPPER、 M5Rules、 OneR、 PART、その他諸々の実装があります。 IF-THEN ルールは、この本のRuleFit algorithmの章で述べられている通り、線形モデルで使用できます。
Holte, Robert C. "Very simple classification rules perform well on most commonly used datasets." Machine learning 11.1 (1993): 63-90.↩
Cohen, William W. "Fast effective rule induction." Machine Learning Proceedings (1995). 115-123.↩
Letham, Benjamin, et al. "Interpretable classifiers using rules and Bayesian analysis: Building a better stroke prediction model." The Annals of Applied Statistics 9.3 (2015): 1350-1371.↩
Borgelt, C. "An implementation of the FP-growth algorithm." Proceedings of the 1st International Workshop on Open Source Data Mining Frequent Pattern Mining Implementations - OSDM ’05, 1–5. http://doi.org/10.1145/1133905.1133907 (2005).↩
Yang, Hongyu, Cynthia Rudin, and Margo Seltzer. "Scalable Bayesian rule lists." Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.↩
Fürnkranz, Johannes, Dragan Gamberger, and Nada Lavrač. "Foundations of rule learning." Springer Science & Business Media, (2012).↩