6.3 prototype と criticism

prototype は、すべてのデータの代表であるデータインスタンスです。 criticism は prototype の集まりではうまく表現できないデータインスタンスです。 criticism の目的は、特に、prototype が良く表現できないデータ点について、prototype とともに見識を提供することです。 prototype と criticism は、データを記述するのに機械学習モデルとは独立に使用可能ですが、解釈可能なモデルを作成したり、ブラックボックスモデルを解釈可能にするために使用できます。

この章では、1つのインスタンスを指すときや、あるインスタンスはそれぞれの特徴量の次元である座標系における1つの点でもあることの説明を強調するために "データ点" という表現を使います。 次の図は、シミュレーションによるデータの分布を示していて、prototype として、または criticism として選択されたインスタンスもいくつかあります。 小さな点はデータ、大きな点は criticism で、大きな四角形は prototype です。 prototype はデータ分布の中央を覆うように(手動で)選択されていて、criticism は prototype を除くクラスタ内の点です。 prototype と criticism は常に実際のデータに含まれるインスタンスです。

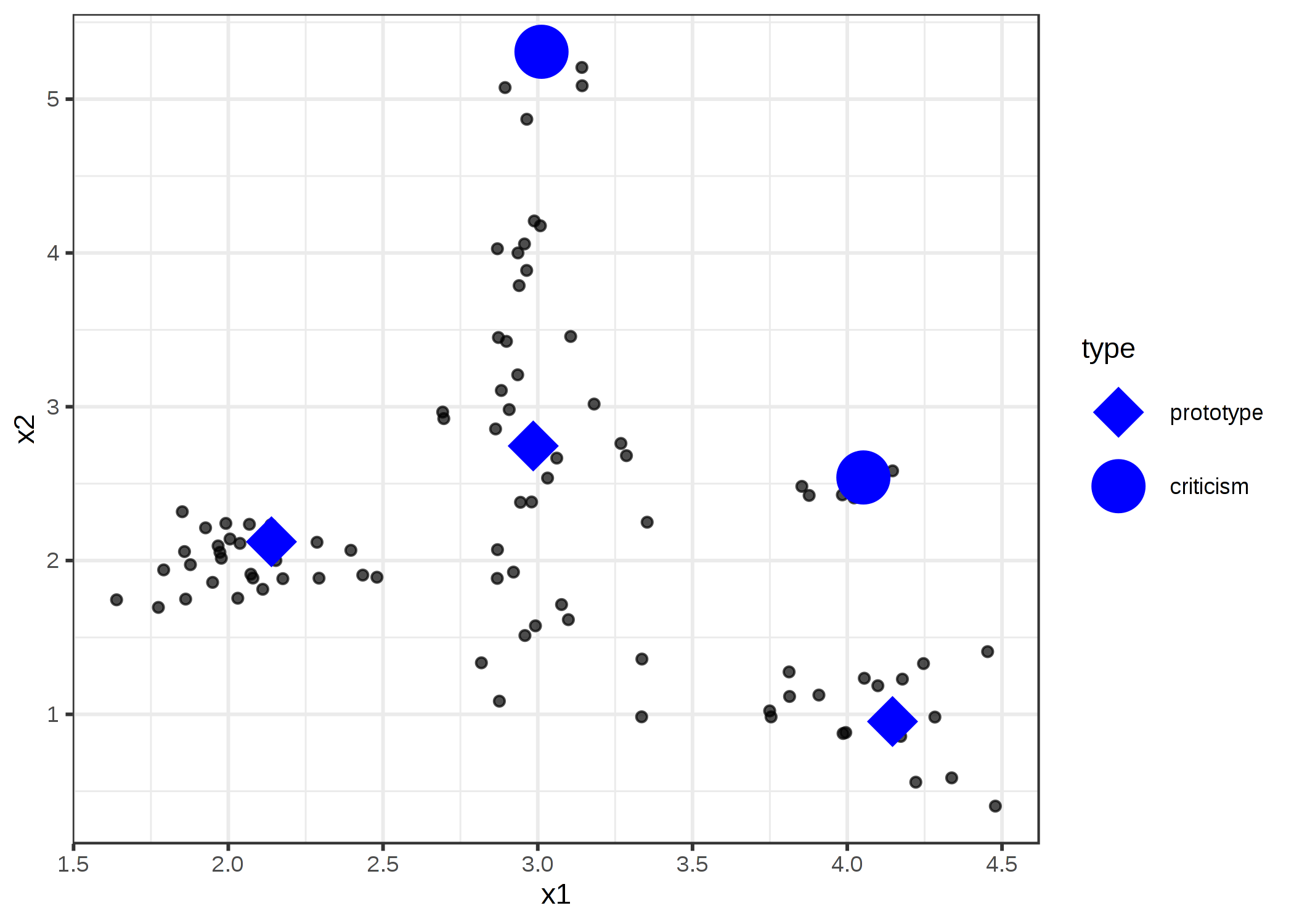
2つの特徴量 x1 と x2 を持つデータ分布の prototype と criticism。

FIGURE 6.6: 2つの特徴量 x1 と x2 を持つデータ分布の prototype と criticism。

手作業で prototype を選びましたが、これは上手くスケールせず悪い結果になりそうです。 データの中から prototype を見つけるためのアプローチはたくさんあります。 そのうちの1つが k-medoids であり、k-means アルゴリズムに関連するクラスタリングアルゴリズムです。 クラスタの中心として実際のデータ点を返すようなクラスタリングアルゴリズムであれば prototype の選択に適しているでしょう。 しかし、それらの手法の殆どは prototype しか見つけることができず、criticism は見つけられません。 この章では、Kim et.al (2016)61 による MMD-critic という、prototype と criticism を1つのフレームワークに組み合わせたアプローチを紹介します。

MMD-critic は、データの分布と選択された prototype の分布を比較します。 これが MMD-critic を理解するための中心的な概念です。 MMD-critic は、2つの分布間の差異を最小化するような prototype を選択します。 密度の高い領域のデータ点、特に、異なる"データクラスタ"から選ばれたとき、良い prototype となります。 prototype ではうまく説明できない範囲から得られるデータ点は criticism として選択されます。

理論を深掘りしましょう。

6.3.1 理論

高レベルでの MMD-critic の手順は以下のように簡潔にまとめられます。

  1. 見つけたい prototype と criticism の数を選びます。
  2. prototype を貪欲法で探索します。 prototype の分布がデータの分布と近くなるように prototype は選択されます。
  3. criticism を貪欲法で探索します。 prototype の分布とデータの分布が異なる点は criticism として選択されます。

データセットにおける prototype と criticism を MMD-critic によって見つけるために必要な構成要素がいくつかあります。 最も基本的な要素として、データの密度を推定するためにカーネル関数が必要です。 カーネルは2つのデータ点の近さに応じて重み付けする関数です。 密度推定に基づいて、選択された prototype の分布がデータの分布と近いかどうか知るために、2つの分布がどれだけ異なるのかを知る基準が必要です。 これは、 maximum mean discrepancy(MMD) を測ることで解決します。 また、カーネル関数に基づいて、特定のデータ点において2つの分布がどれだけ異なるのか知るための witness 関数が必要です。 prototype とデータの分布が乖離していて、witness 関数が大きな絶対値をとるデータ点を criticism として選択できます。 最後の要素は、良い prototype と criticism のための探索戦略であり、単に貪欲探索によって解決します。

2つの分布の違いを測る maximum mean discrepancy(MMD) から初めていきましょう。 prototype の選択によって prototype の密度分布を作ります。 我々は prototype の分布がデータの分布と異なるのかどうか評価したいです。 カーネル密度関数によってその両方を推定します。 maximum mean discrepancy は2つの分布間の差異を測る指標です。これは2つの分布に対応する期待値間の差異を表す関数空間上での上界です。 わかるでしょうか。 個人的に、これらの概念は、データからどんなものが計算されるのかを見た方が遥かに良く理解できます。 次の式は、MMD の二乗(MMD2)の計算方法を示しています。

\[MMD^2=\frac{1}{m^2}\sum_{i,j=1}^m{}k(z_i,z_j)-\frac{2}{mn}\sum_{i,j=1}^{m,n}k(z_i,x_j)+\frac{1}{n^2}\sum_{i,j=1}^n{}k(x_i,x_j)\]

k は2点の類似度を測るカーネル関数ですが、これについては後述します。 m は prototype である z の数で、n は元々のデータセット上のデータ点 x の数です。 prototype の z はデータ点 x から選ばれたものです。 それぞれの点は多次元なので、複数の特徴量を持つことができます。 MMD-critic の目的は MMD2 を最小化することです。 MMD2 がゼロに近いほど、prototype の分布はデータによくフィットします。 MMD2 をゼロに近づける鍵となるのは中央の項で、これは prototype と全てのデータ点との平均的な（2乗された）近さを計算します。 この項と、最初の項（prototype どうしの平均的な近さ）に加え、最後の項（データどうしの平均的な近さ）を足し上げれば、prototype はデータを完璧に説明できます。 n 個全てのデータ点を prototype として使った時、この式に何がどうなるのか試してみてください。

次の図は、MMD2 measure を表現しています。 最初の図は、データ点を2つの特徴量で示していて、推定データ密度を背景にグラデーションで表現しています。 その他はそれぞれ異なる prototype の選択をしていて、その時の MMD2 measure を図の上部に記しています。 prototype は大きなドットで、その分布は等高線で表しています。 これらの中で最もデータを覆っている prototype の選択は（左下）最も低い乖離度になっています。

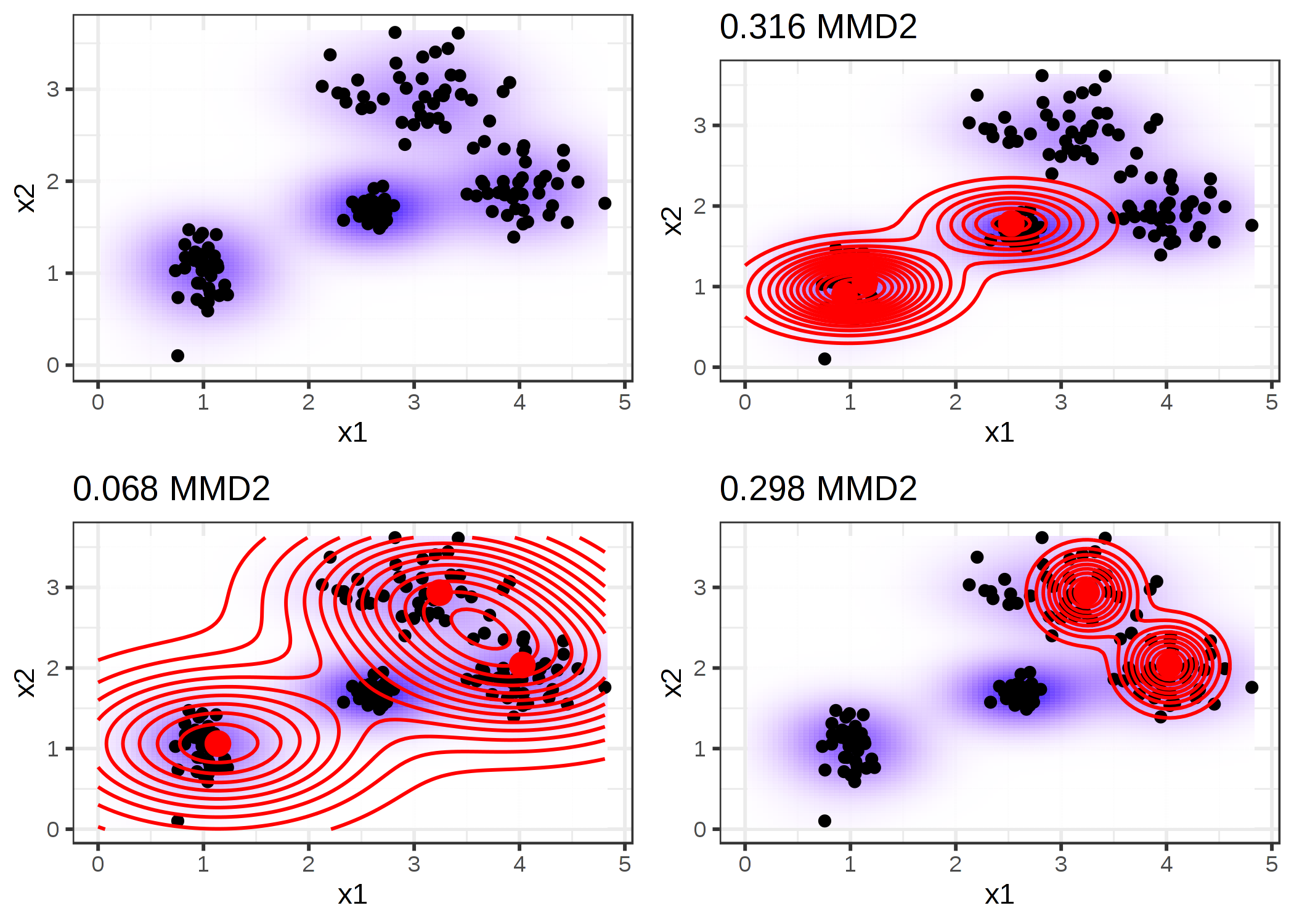
二つの特徴量を持つデータセットに対する異なる prototype の MMD の二乗(MMD2)

FIGURE 6.7: 二つの特徴量を持つデータセットに対する異なる prototype の MMD の二乗(MMD2)

カーネルの選択は動径基底関数カーネルです。

\[k(x,x^\prime)=exp\left(-\gamma||x-x^\prime||^2\right)\]

ここで、||x-x'||2 は2点間のユークリッド距離で \(\gamma\) はスケールパラメータです。 カーネルの値は2点間の距離に応じて減少し、0と1の範囲に収まります。 2点間が無限遠にある時に 0 になり、同じ点にある時 1 になります。

prototype を見つけるためのアルゴリズムとして MMD2、カーネル、貪欲法を組み合わせます。

  • prototype の空のリストを用意します。
  • prototype の数は選ばれた m 個以下として、
    • データセット上のそれぞれの点が prototype のリストに追加された時に MMD2 がどのくらい減少するのか確認します。MMD2 を最小化するようなデータ点をリストに追加します。
  • prototype のリストを返します。

criticism を探すための残りの成分は、ある点での2つの推定密度がどのくらい異なるのか知るための witness 関数になります。 これは次のように推定できます。

\[witness(x)=\frac{1}{n}\sum_{i=1}^nk(x,x_i)-\frac{1}{m}\sum_{j=1}^mk(x,z_j)\]

2つの同じ特徴量を持つデータセットがある時、witness関数は、点 x がどちらの経験的分布に良く適合するかを評価する手段となります。 criticism を見つけるために、witness 関数の外れ値を正負どちらの方向についても探します。 witness 関数の最初の項は点 x とデータの類似度の平均で、同様に、2番目の項はデータ点と prototype 間の類似度の平均です。 ある点 x での witness 関数が 0 に近づくと、データとプロトタイプの密度関数は互いに近づきます。これはプロトタイプの分布が点 x でのデータの分布と類似することです。 witness 関数が点 x で負であるとき、prototype の分布はデータの分布を過大評価しています(例えば、prototype を1つ選んだのに近くにデータ点が少ししかない時など)。 一方、正のとき、プロトタイプの分布はデータの分布を過小評価しています(例えば、x の周りのデータ点が沢山あるのに、近くの prototype を1つも選ばないなど)。

より直感的に理解するために、先ほどプロットした prototype のうち最も小さな MMD2 をもつものを再利用して、いくつか手動で選んだ点に対する witness 関数を表示してみましょう。 次の図のラベルは、三角形で表された様々な点に関する witness 関数の値を示しています。 中央の点のみが大きな絶対値をもつことから、criticism として良い候補になります。

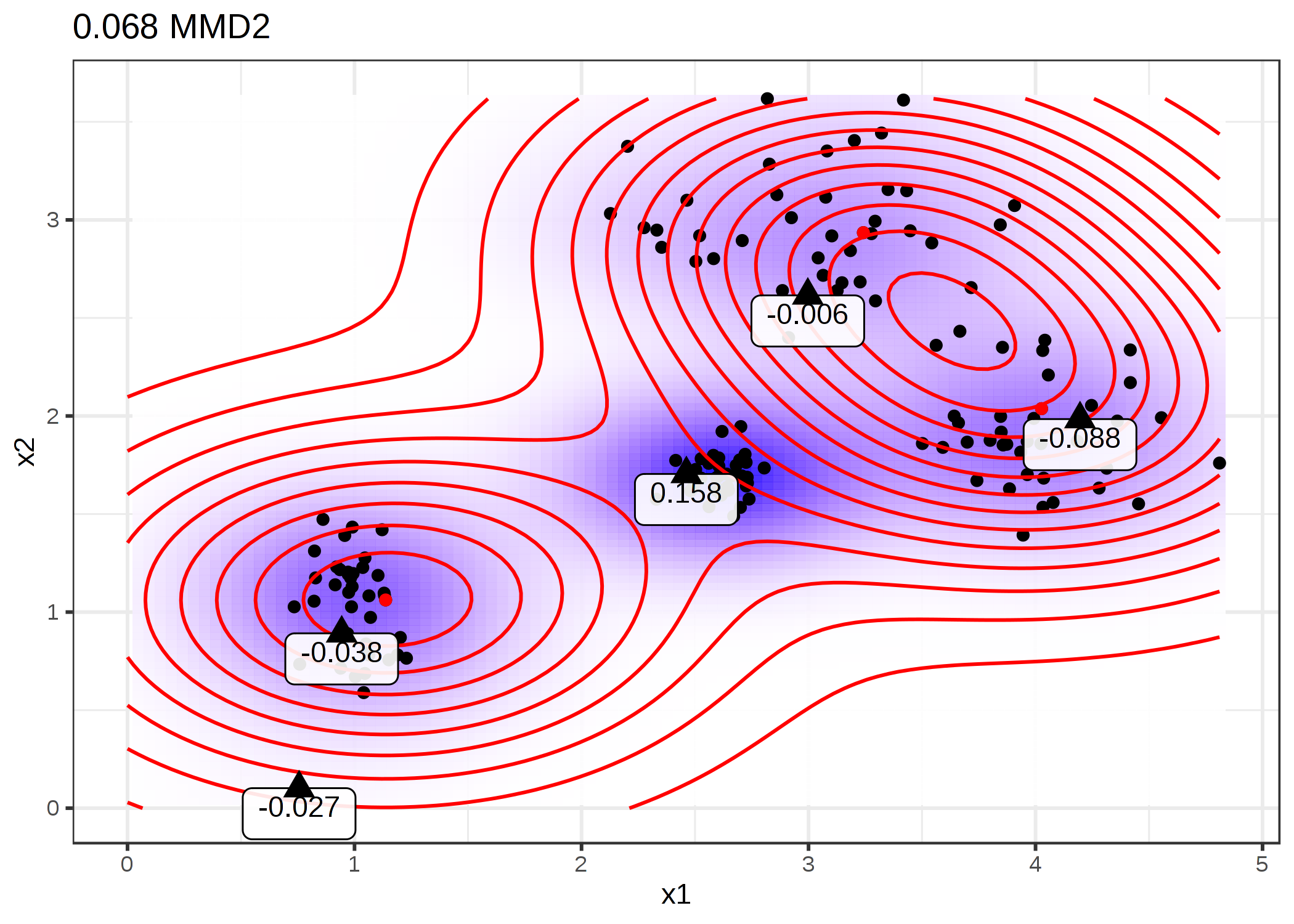
異なる点における witness 関数の評価

FIGURE 6.8: 異なる点における witness 関数の評価

witness 関数を使うことで、prototype によって上手く表されていないデータインスタンスを明示的に探すことができます。 criticism は witness 関数の出力の中で、高い絶対値を持つ点のことを言います。 prototype と同様に、criticism も貪欲法により探索されます。 しかし、全体の MMD2 を減らすのではなく、witness 関数と正則化項を含むコスト関数を最大化する点が探されます。 正則化項は、異なるクラスターから点が選択されるよう、点の多様性を強制します。

この2つ目のステップは、prototype の決定方法とは独立しています。 criticism を学ぶため、ここで述べた手順といくつかの prototype を選んでみます。 もしくは、prototype は、例えば k-medoids のようなクラスタリング手法により選択できます。

これで、MMD-critic 理論の重要な部分は以上です。 ただし、1つ疑問が残されています。 機械学習の解釈性に、MMD-criticはどのように使われるのかということです。

MMD-critic は、1) データの分布の理解に役立つ、2) 解釈可能なモデルを構築する、3) ブラックボックスを解釈可能にする という3つの観点で、解釈性に寄与します。 prototype と criticism を探すために、データセットに MMD-critic を適用すると、データへの理解が深まります。 しかし、MMD-critic を用いると、さらに期待できることがあります。

例えば、解釈可能な予測モデルを作ることもできます。 これを"nearest prototype model"と呼びましょう。 この予測モデルは以下のように定義されます。

\[\hat{f}(x)=argmax_{i\in{}S}k(x,x_i)\]

このモデルは、カーネル関数の出力が大きいという意味で、新しいデータに最も近い prototype が S から選ばれるという意味になります。 prototype 自体は、予測結果に対する説明として考えられます。 この方法には、カーネルの種類、カーネルのスケールパラメータ、prototypeの数という3つのハイパーパラメータがあります。

全てのパラメータは、クロスバリデーションで最適化できます。 criticism はこのアプローチでは使われません。

3つ目の MMD-critic の使い方として、prototype と criticism により任意の機械学習モデルを大域的に説明可能にできます。 方法としては、次の通りです。

  1. prototype と criticism を MMD-critic を用いて探索
  2. 機械学習モデルを学習
  3. prototype と criticism に対して、学習された機械学習モデルを用いて、予測結果を取得
  4. 予測結果を解析: どのケースでモデルは予測を間違えたのか。 これにより、機械学習モデルの弱点を見つけることができ、またデータをよく表現するいくつからのサンプルを見つけることができます。

これはどのような意味があるでしょうか。 Google の画像分類モデルが、黒人をゴリラとして分類した問題を思い出してください。 おそらく、彼らは、画像認識モデルをデプロイする前に、これらの手法を適用するべきだったのでは無いでしょうか。 99% 正しくても、この問題は残りの 1% にある問題なので、モデルの性能を確認するだけでは、不十分です。 そして、ラベルも間違っていることがあります。 全ての学習データを通して、予測結果に問題が無いか確認していれば、この問題は事前に明らかになったかもしれませんが、それは不可能です。 しかし、数千程度の prototype と ciriticisms を選択と確認し、データに関する問題を明らかにしたでしょう。 肌の黒い人の画像が少なく、つまりデータセットの多様性に問題があることを事前に明らかにできたかもしれません。 あるいは、肌の色が濃い人を prototype として、あるいは悪名高い「ゴリラ」という分類で criticism として、1つ以上の画像を表示していたかもしれません。 MMD-critic が確実にこの類のミスを取り除くとは約束できませんが、よいチェックにはなるでしょう。

6.3.2 例

MMD-critic の次の例では、手書き数字データセットを使っています。

実際の prototype の見ると、数字ごとの画像の枚数が異なることに気づくかもしれません。 これはクラスごとに固定の数を決めて prototype を選んだ訳ではなく、データセット全体で固定の数を決めて prototype を選んだためです。 予想通り、prototype は各数字の異なる書き方のものが選ばれています。

手書き数字データセットにおける prototype

FIGURE 6.9: 手書き数字データセットにおける prototype

6.3.3 長所

ユーザ研究において、MMD-critic の著者は参加者に画像を与えました。参加者は（犬種など）2つのクラスの1つをそれぞれ表す二枚の画像の内、視覚的にマッチする一枚を選ぶ必要があります。 参加者は、ランダムな画像ではなく、prototype と criticism である画像を与えらた場合に、最高のパフォーマンスを示しました。

prototype と criticism の数は自由に選ぶことができます。 MMD-critic はデータの密度推定にも使えます。 また、MMD-critic はどんなタイプのデータでも、どんなタイプの機械学習モデルにも使うことができます。

アルゴリズムの実装も簡単です。

MMD-critic は解釈性を高めるために使う方法において非常に柔軟です。 複雑なデータ分布を理解するために使用できます。 解釈可能な機械学習モデルを作るために使用できます。 あるいは、black box モデルを理解するために役立ちます。

criticisms を見つけることは、prototype を選ぶプロセスとは独立しています。 しかし、MMD-critic に従って prototype を選ぶことは理にかなっています。なぜなら、prototype も criticisms も、prototype とデータ密度を比較する同じ方法で作れられるためです。

6.3.4 短所

数学的には、prototype と criticism は異なる定義ですが、これらの違いは、カットオフ値（prototype の数）に基づいています。 データの分布をカバーするために、少ない数の prototype を選択したとします。 この場合、criticisims はうまく説明されていない部分に集中してしまいます。 しかし、より多くの prototype を追加したとしても、同じ範囲に集まってしまうでしょう。 どのような解釈をするにしても、criticisims は prototype の数を決定する（任意の）カットオフ値と既存の prototype に強く依存することを考慮に入れる必要があります。

prototype と criticisims の数を選ぶ必要があります。 これはメリットにもなりますが、デメリットにもなります。 どの程度の prototype と criticism の数が実際必要でしょうか。 さらに多い方が良いのでしょうか、それとも少ない方が良いのでしょうか。 1つの答えは、人がどれくらいの時間で画像を見ているかを計測することで、prototype と criticism を決める方法です。

MMD-critic を用いて分類器を作成する場合、直接最適化する方法があります。 1つの解決手段は、横軸に prototype の数をとり、縦軸に MMD2 の値をプロットして見てみることです。 こうすることで、MMD2 カーブがフラットになったところで、prototype の数を選ぶことができます。

他のパラメータは、カーネルとカーネルのスケールパラメータになります。 ここで、prototype と criticism の数の場合と同様の問題があります。 どのようにカーネルとカーネルのスケールパラメータを選べば良いでしょうか。 繰り返しになりますが、MMD-critic を最も近い prototype を返す分類器として使う場合、カーネルパラメータも調整できます。 しかし、MMD-critic の教師なしにおけるユースケースの場合、明らかではありません。 全ての教師なし手法は同様の問題を抱えているため、少し難しいかもしれません。

これは、すべての特徴量を入力として受け取り、いくつかの特徴量が関心のある結果を予測するために関連性がないかもしれないという事実を無視しています。 1つの解決策は、生の画像の代わりに、例えば画像の埋め込みなどの関連する特徴量のみを使うことです。 これは、元のインスタンスを、関連する情報のみを含む表現に射影する方法がある場合のみ有効です。

利用できるコードはありますが、綺麗にパッケージ化され、かつドキュメントがあるものはまだありません。

6.3.5 コードと代替手法

MMD-critic の実装は以下にあります。 https://github.com/BeenKim/MMD-critic.

prototype を見つけるための、最もシンプルな代替手法は以下です。 k-medoids by Kaufman et. al (1987).62

  1. Kim, Been, Rajiv Khanna, and Oluwasanmi O. Koyejo. "Examples are not enough, learn to criticize! Criticism for interpretability." Advances in Neural Information Processing Systems (2016).↩

  2. Kaufman, Leonard, and Peter Rousseeuw. "Clustering by means of medoids". North-Holland (1987).↩